Урок 1 Числовые выражения
 Скачать 2.02 Mb.
|
|
III. Формирование умений и навыков. 1-я группа. Упражнения на применение формул нахождения медианы упорядоченного и неупорядоченного ряда. 1. № 186. Решение: а) число членов ряда п = 9; медиана есть среднее в упорядоченном ряду значение варианта Ме = 41; б) п = 7, ряд упорядочен, Ме = 207; в) п = 6, ряд упорядочен, Ме =  = 21;г) п = 8, ряд упорядочен, Ме =  = 2,9.Ответ: а) 41; б) 207; в) 21; г) 2,9. 3. № 188 (устно). Решение: а) Может, если сумма членов не кратна числу членов. б) Не может, так как разность двух натуральных чисел, из которых уменьшаемое больше вычитаемого, есть натуральное число. в) Не может, так как мода – один из членов ряда, а все члены ряда – натуральные числа. г) Может, если число членов ряда четное и числа  и  не равны между собой.Ответ: да; б) нет; в) нет; г) да. 4. Зная, что в упорядоченном ряду содержится т чисел, где т – нечетное число, укажите номер члена, являющегося медианой, если т равно: а) 5; б) 17; в) 47; г) 201. Решение: Номер находим как  + 1, где – целая часть числа.а)  + 1 = 2 + 1 = 3; в)  + 1 = 23 + 1 = 24;б)  + 1 = 8 + 1 = 9; г)  + 1 = 100 + 1 = 101.Ответ: а) 3; б) 9; в) 24; г) 101. 2-я группа. Практические задачи на нахождение медианы соответствующего ряда и интерпретацию полученного результата. 1. № 189. Решение: Число членов ряда п = 12. Для нахождения медианы ряд нужно упорядочить: 136, 149, 156, 158, 168, 174, 178, 179, 185, 185, 185, 194. Медиана ряда Ме =  = 176.Выработка за месяц была больше медианы у следующих членов артели: 1) Квитко; 4) Бобков; 2) Баранов; 5) Рылов; 3) Антонов; 6) Астафьев. Ответ: 176. 2. № 192. Решение: Упорядочим ряд данных: 30, 31, 32, 32, 32, 32, 32, 32, 33, 35, 35, 36, 36, 36, 38, 38, 38, 40, 40, 42; число членов ряда п = 20. Размах A = xmax – xmin = 42 – 30 = 12. Мода Мо = 32 (это значение встречается 6 раз – чаще других). Медиана Ме =  = 35.Размах показывает наибольший разброс времени на обработку детали; мода показывает наиболее типическое значение времени обработки; медиана – время обработки, которое не превысили половина токарей. Ответ: 12; 32; 35. IV. Итоги урока. – Что называется медианой ряда чисел? – Может ли медиана ряда чисел не совпадать ни с одним из чисел ряда? – Какое число является медианой упорядоченного ряда, содержащего 2п чисел? 2п – 1 чисел? – Как найти медиану неупорядоченного ряда? Домашнее задание: № 187, № 190, № 191, № 254. Урок 23 Использование средних статистических характеристик при решении различных задач Цели: продолжить формировать умение использовать средние статистические характеристики (размах, мода, среднее арифметическое, медиана) при решении различных задач (вычисление и интерпретация). Ход урока I. Устная работа. 1. Педагогический стаж восьми учителей школы, работающих в старших классах одной школы, следующий: 5 лет, 8 лет, 15 лет, 12 лет, 8 лет, 14 лет, 18 лет, 9 лет. Найдите моду и медиану этой выборки. 2. Найдите среднее арифметическое и размах ряда: 2; 3; 5; 6; 14; 15; 17; 18. II. Проверочная работа. Вариант 1 1. Найдите медиану упорядоченного ряда: а)  ;б) 11, 12, 18, 23, 29, 31, 37, 42. 2. Найдите медиану неупорядоченного ряда: 8, 11, 4, 17, 35, 21, 19, 50. Вариант 2 1. Найдите медиану упорядоченного ряда: а)  ;б) 0,5; 1,2; 1,8; 2,5; 3,5; 4,8; 5,1; 5,9. 2. Найдите медиану неупорядоченного ряда: 21, 13, 18, 11, 27, 32, 23, 41. III. Формирование умений и навыков. На данном уроке обобщаются знания по теме «Статистические характеристики» и учащимся предлагаются задания на нахождение всех характеристик и их интерпретацию в зависимости от условия задачи. Кроме того, сильным учащимся можно предложить для решения задачи повышенной сложности. В конце занятия целесообразно привести пример, показывающий необходимость критического отношения к полученным результатам. 1. В таблице показано число посетителей выставки в разные дни недели:
Найдите медиану указанного ряда данных. В какие дни недели число посетителей выставки было больше медианы? Решение: Число членов в ряду п = 7. Для нахождения медианы упорядочим ряд: 604, 615, 625, 636, 638, 710, 724. Медиана Ме = 636. Число посетителей было больше медианы во вторник, субботу и воскресенье. Ответ: 636; вторник, суббота, воскресенье. 2. Ниже указана среднесуточная переработка сахара (в тыс. ц) заводами сахарной промышленности некоторого региона: 12,2; 13,2; 13,7; 18,0; 18,6; 12,2; 18,5; 12,4; 14,2; 17,8. Для представленного ряда данных найдите среднее арифметическое, моду, размах и медиану. Что характеризует каждый из этих показателей? Решение: Число членов ряда п = 10. Упорядочим ряд: 12,2; 12,2; 12,4; 13,2; 13,7; 14,2; 17,8; 18,0; 18,5; 18,6. Среднее арифметическое характеризует средний уровень значений и общую сумму всех значений: х = 15,08. Мода Мо = 12,2 показывает значение, встречающееся чаще других (в данном случае слабо выражена, значение 12,2 встречается только 2 раза). Размах A = xmax – xmin = 18,6 – 12,2 = 6,4 характеризует величину разброса наблюдаемых значений. Медиана Me =  = 13,95 показывает, что половина членов ряда не превосходит по величине 13,95.Ответ: 15,08; 12,2; 6,4; 13,95. 3. Девочки седьмого класса на уроке физкультуры при прыжках взяли высоты, величины которых (в см) учитель записал в журнал: 90; 125; 125; 130; 130; 135; 135; 135; 140; 140; 140. Какая высота прыжка наилучшим образом характеризует спортивную подготовку девочек класса? Решение: Ряд наблюдений упорядочен: п = 11. Ряд имеет две моды: Мо1 = 135, Мо2 = 140. Среднее арифметическое ряда равно х 129,5. Медиана Ме = 135. Наилучшей характеристикой спортивной подготовки девочек следует признать медиану: мода неоднозначна (135 и 140), а среднее значение занижено за счет одного очень плохого результата 90 см (если этот результат отбросить, то х = 133,5 см). Ответ: 135 см. 5. Владелец одного частного предприятия уволил бльшую часть рабочих, а оставшимся снизил зарплату на 20 %. После этого он заявил, что средний заработок его рабочих повысился. Так ли это?
Решение: Вычисляем средние статистические характеристики: мода до увольнения Мо = 400; мода после увольнения Мо = 800; медиана до увольнения Ме = 400; медиана после увольнения Ме = 800; среднее арифметическое до увольнения X =  = 520;после увольнения X =  = 620.Вычисления подтверждают, что средние характеристики действительно увеличились. Однако простой взгляд на таблицу подтверждает, что жизнь рабочих не улучшилась, а, наоборот, ухудшилась! Не говоря уже о тех, кто потерял работу. Здесь итоги решения математической задачи противоречат здравому смыслу. Математическая модель не всегда адекватна практической ситуации. В данном случае средние характеристики не являются типичными представителями статистических данных, поэтому их использование приводит к ложному выводу. На примере этой задачи показываем учащимся, что необходимо не только формально вычислять средние характеристики, но и уметь правильно истолковывать статистическую информацию. IV. Итоги урока. Домашнее задание: 1. Найдите размах, моду и медиану ряда: а) 1; 3; –2; 4; –2; 0; 2; 3; 1; –2; 4; б) 0,2; 0,4; 0,1; 0,5; 0,1; 0,2; 0,3; 0,5; 0,4; 0,6. 2. В вашем (или соседнем) классе соберите данные о месяцах рождения учеников. Месяцы удобнее перечислять не по названиям, а по номерам. Найдите: а) размах; б) моду; в) среднее арифметическое для экспериментальной выборки. 3. Для упорядоченного ряда, содержащего т чисел, где т – четное число, укажите номера двух последовательных членов, между которыми заключена медиана, если т равно: а) 6; б) 18; в) 56; г) 240. Урок 25 Контрольная работа № 2 «Уравнение с одной переменной» Вариант 1 1. Решите уравнение. а)  x = 12; в) 5x – 4,5 = 3x + 2,5;б) 6x – 10,2 = 0; г) 2x – (6x – 5) = 45. 2. Таня в школу сначала едет на автобусе, а потом идет пешком. Вся дорога у неё занимает 26 мин. Идет она на 6 мин дольше, чем едет на автобусе. Сколько минут она едет на автобусе? 3. В двух сараях сложено сено, причем в первом сарае сена в 3 раза больше, чем во втором. После того как из первого сарая увезли 20 т сена, а во второй привезли 10 т, в обоих сараях сена стало поровну. Сколько всего тонн сена было в двух сараях первоначально? 4. Решите уравнение 7x – (x + 3) = 3(2x – 1). Вариант 2 1. Решите уравнение. а)  x = 18; в) 6x – 0,8 = 3x + 2,2;б) 7x + 11,9 = 0; г) 5x – (7x + 7) = 9. 2. Часть пути в 600 км турист пролетел на самолете, а часть проехал на автобусе. На самолете он проделал путь в 9 раз больший, чем на автобусе. Сколько километров турист проехал на автобусе? 3. На одном участке было в 5 раз больше саженцев смородины, чем на другом. После того как с первого участка увезли 50 саженцев, а на второй посадили еще 90, на обоих участках саженцев стало поровну. Сколько всего саженцев было на двух участках первоначально? 4. Решите уравнение 6x – (2x – 5) = 2(2x + 4). Урок №25 Что такое функция? Цели: ввести понятие функциональной зависимости; дать определения независимой переменной (аргумента), зависимой переменной, области определения функции, области значений функции. Ход урока Организационный момент I. Устная работа. 1. Найдите значение выражения. а) 3x – (2 + 3x) при х = 7,862; б) 2a – (a – 0,3) при а = 0,7; 2. Решите уравнение. а) 3х = –9; б)  ; в) 5а – 15 = 0;г) 3х = 3х + 11; д)  (x – 8); е) 3y +  = 0.II. Объяснение нового материала. 1. Основная задача первого занятия: показать, что функция – это математическая модель, позволяющая описывать и изучать разнообразные зависимости между реальными величинами. Функция имеет общекультурное, мировоззренческое значение. При её изучении учащиеся знакомятся с идеей всеобщей связи, идеей непрерывности, бесконечности, интерполяции. 2. Объяснение проводить согласно пункту 12 учебника. Необходимо привести достаточно примеров функциональной зависимости (учебник, с. 51–53). Также нужно не только показывать зависимости, но и сразу обсуждать, в какой области человеческой деятельности применяются такие функциональные зависимости. 3. Вводим понятия независимой и зависимой переменных и определение функции как зависимости одной переменной от другой. На примерах показываем, что область определения функции может быть бесконечным и конечным множеством чисел. III. Формирование умений и навыков. Все задания, решаемые на этом уроке, направлены на усвоение как самого понятия функции, так и различных способов её задания (словесный, с помощью формулы, табличный, графический). Ученики должны уметь переходить от одного вида задания к другому и находить значения функции при каждом способе задания. 1. № 258, № 260. 2. Функция задана формулой у = 2 – 5х, верны ли равенства: а) у = 12 при х = –2; б) у = 3 при х =  ;в) у = 20 при х = 4; г) у = –0,5 при х =  ?3. № 261. 4. Функция задана графиком: 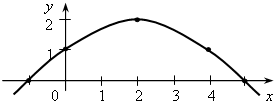 а) Найти значения функции при х = 0; 2; 3,5; –1. б) При каком значении х значение функции равно 1; 2; 0? в) Назвать несколько значений х, при которых значение функции положительно. г) Назвать несколько значений х, при которых значение функции отрицательно. 5. Устно. Результаты измерений температуры воздуха за сутки даны в следующей таблице:
а) Назовите температуру в 6 ч, 8 ч, 24 ч. б) В какое время температура была равна +1°, –4°, 11°? в) Почему эту зависимость можно назвать функцией? 6. № 263. Решение: Если r – остаток от деления натурального числа п на 4, то можно записать n = 4 · x + r, где 0 ≤ r < 4. Найдем соответствующие значения r: а) Если п = 13, то 13 = 3 · 4 + 1, то есть r = 1; б) если п = 34, то 34 = 8 · 4 + 2, то есть r = 2; в) если п = 43, то 43 = 10 · 4 + 3, то есть r = 3; г) если п = 100, то 100 = 25 · 4 + 0, то есть r = 0. В рассматриваемой функциональной зависимости аргументом является переменная п. Областью определения является множество чисел {13; 34; 43; 100}. Значениями функции служат числа 0; 1; 2; 3. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
