Урок 1 Числовые выражения
 Скачать 2.02 Mb.
|
|
Ход урока I. Организационный момент II. Формирование умений и навыков. 1. № 158. Решение: Анализ условия: 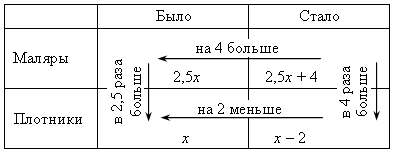 Пусть х плотников было в бригаде, тогда маляров было 2,5х. После переводов в бригаде стало (2,5х + 4) маляров и (х – 2) плотников. Зная, что маляров стало в 4 раза больше плотников, составим уравнение: (2,5х + 4) = 4 · (х – 2); 2,5х + 4 = 4х – 8; 2,5х – 4х = –8 – 4; –1,5х = –12; х = (–12) : (–1,5); х = 8. Значит, в бригаде было 8 плотников. Так как 2,5х = 2,5 · 8 = 20, то в бригаде было 20 маляров. Ответ: 20 маляров и 8 плотников. В таблице основную зависимость, по которой формируем равенство, можно выделить другим цветом или более жирной линией. 2. № 161. Решение: Анализ условия: 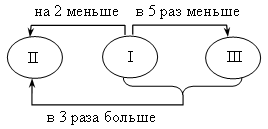 Пусть х кг – масса первого арбуза, тогда второй арбуз весит (х + 2) кг, а третий – 5х кг. Первый и третий арбуз вместе весят х + 5х, то есть 6х кг. Зная, что в сумме они весят в 3 раза больше второго арбуза, составим уравнение: 3 · (х + 2) = 6х; 3х + 6 = 6х; 3х – 6х = –6; –3х = –6; х = 2. Значит, первый арбуз весит 2 кг. Так как х + 2 = 2 + 2 = 4, то второй арбуз весит 4 кг. Так как 5 · х = 5 · 2 = 10, то третий арбуз весит 10 кг. Ответ: 2 кг, 4 кг, 10 кг. 3. № 162. Решение: Анализ условия:
Пусть х кг сахара взяли из первого мешка, тогда из второго мешка взяли 3х кг сахара. В первом мешке осталось (50 – х) кг сахара, а во втором – (50 – 3х) кг. Зная, что во втором мешке осталось в 2 раза меньше сахара, чем в первом, составим уравнение: 2 · (50 – 3х) = 50 – х; 100 – 6х = 50 – х; –6х + х = 50 – 100; –5х = –50; х = (–50) : (–5); х = 10. Значит, из первого мешка взяли 10 кг сахара. Так как 50 – х = = 50 – 10 = 40, то в первом мешке осталось 40 кг сахара. Так как 50 – 3х = = 50 – 3 · 10 = 50 – 30 = 20, то во втором мешке осталось 20 кг сахара. Ответ: 40 кг и 20 кг. 4. Федя на 7 лет старше Пети, а их папе в 3 раза больше лет, чем им обоим вместе. Сколько лет каждому из них, если папе было 36 лет, когда родился Петя? Решение: Анализ условия:  Пусть х лет Пете, тогда Феде (х + 7) лет, а папе (х + 36) лет. Пете и Феде вместе х + (х + 7) лет или 2х + 7 лет. Зная, что папе лет в 3 раза больше, чем им обоим вместе, составим уравнение: (2х + 7) · 3 = х + 36; 6х + 21 = х + 36; 6х – х = 36 – 21; 5х = 15; х = 3. Значит, Пете 3 года. Так как х + 7 = 3 + 7 = 10, то Феде 10 лет. Ответ: Пете 3 года, Феде 10 лет. Вариант'>III. Проверочная работа. Вариант 1 Стоимость изделия третьего сорта в 3 раза меньше стоимости изделия первого сорта. Сколько стоит каждое изделие, если изделие первого сорта на 5000 р. дороже изделия третьего сорта? Вариант 2 Мама весит в 5 раз больше дочери, а дочь на 40 кг легче мамы. Сколько весят мама и дочь в отдельности? IV. Итоги урока. Домашнее задание: 1. № 159, № 160, № 252. Урок 20 Среднее арифметическое, размах и мода Цели: ввести понятия таких статистических характеристик, как среднее арифметическое, размах и мода; формировать умение находить средние статистические характеристики различных рядов. Ход урока I. Организационный момент II. Объяснение нового материала. Объяснение следует проводить согласно пункту 9 учебника. Особое внимание следует уделить целесообразности использования различных средних статистических характеристик в зависимости от ситуации. Необходимо подытожить, какие статистические характеристики теперь могут находить учащиеся. Для этого на доску можно вынести пример.
III. Формирование умений и навыков. 1. № 167, № 168. Необходимо, чтобы учащиеся четко мотивировали свои ответы. а) сложили все члены ряда и полученную сумму разделили на их количество. Значит, искали среднее арифметическое. б) Нашли разность между наибольшим и наименьшим числом в ряду, то есть размах ряда. в) Число … встречается наибольшее количество раз, значит, это мода ряда. 2. Даны упорядоченные ряды чисел: а) 1; 1; 2; 3; 4; 5; 6; б)  .Для каждого из них найти среднее арифметическое, размах и моду. 3. Найти среднее арифметическое, размах и моду рядов чисел: а) 1; 2; 5; 2; 3; 4; 2; б) 1; 2; 0; 2; 0; 1; 2; 1; 3; 1. 4. № 170. 5. № 171. Решение: Средний ежемесячный расход электроэнергии находим по формуле среднего арифметического: x =  = 63.Ответ: 63 кВт · ч. IV. Итоги урока. – Какие существуют средние статистические характеристики ряда? – Какой ряд называется упорядоченным? – Что называется размахом ряда? Приведите пример. – Что такое мода ряда? Приведите пример. – Как найти среднее арифметическое ряда? Урок 21 Использование средних статистических характеристик при решении различных задач Цель: продолжить формировать умения находить среднестатистические характеристики ряда (среднее арифметическое, размах, мода) при решении различных задач. Ход урока I. Устная работа. Для упорядоченных рядов: а) 0; 0; 1; 2; 3; б) 1; 2; 2; 2; 3; 3; в) 1; 2; 3; 4; 5; 5 найдите размах, среднее арифметическое, моду. II. Проверочная работа. Вариант 1 1. В таблице приведен возраст сотрудников одного из отделов:
Найдите среднее арифметическое, размах и моду этого ряда. 2*. Постройте ряд из четырех чисел, у которого размах равен 2, а среднее арифметическое равно моде. Вариант 2 1. В таблице приведено количество очков, набранных в чемпионате некоторыми баскетболистами.
Найдите среднее арифметическое, размах и моду этого ряда. 2*. Постройте ряд из четырех чисел, у которого размах равен 2, а среднее арифметическое в два раза больше моды. III. Формирование умений и навыков. 1. № 177. Решение: Среднее арифметическое равно: X =  42,45.Размах A = xmax – xmin = 48 – 36 = 12. Мода М = 45 (встречается 3 раза). Среднее арифметическое – это условная величина (она не целая, хотя число деталей может быть только «целым»); она показывает центр «рассеивания» наблюдаемых величин (сумма отклонений от неё равна нулю); также это можно назвать средней выработкой рабочими деталей. Размах характеризует разброс наблюдаемых значений, а мода показывает, какое число изготовленных деталей встречается чаще всего в данной смене рабочих. Ответ: 42,45; 12; 45. 2. № 179. Решение: Найдем средний балл каждого выпускника по формуле среднего арифметического: Ильин: X =  = 4,4;Семенов: X =  3,5;Романов: X =  = 3,8;Попов: X =  4,7.Чтобы выявить наиболее типичную оценку для каждого выпускника, найдем для каждой совокупности моду, то есть оценку, встречающуюся чаще других: Ильин: М = 4 (9 раз из 15); Семенов: М = 3 (9 раз из 15); Романов: М = 4 (10 раз из 15); Попов: М = 5 (10 раз из 15). Использованы среднее арифметическое и мода. Ответ: 4,4 и 4; 3,5 и 3; 3,8 и 4; 4,7 и 5. 3. № 180. Решение: Средняя урожайность пшеницы в хозяйстве равна общему сбору зерна, деленному на общую площадь полей; общий сбор зерна равен 18 ц/га · 12 га + 19 ц/га · 8 га + 23 ц/га · 6га = 506 ц, а общая площадь участков равна 12 га + 8 га + 6 га = 26 га. Средняя урожайность в хозяйстве  19,5 ц/га.Нельзя находить среднюю урожайность как  = 20 (ц/га), так как значения 18, 19 и 23 характеризуют участки разной величины и их «вклад» в общую урожайность зависит от площади каждого участка.Ответ: 19,5 ц/га. 4. № 181. Решение: Среднее арифметическое равно: X =  = 1,7.Размах равен: A = xmax – xmin = 3 – 0 = 3. Мода равна: М = 4 (встречается 4 раза из 10). Среднее арифметическое показывает среднее количество бракованных деталей. Размах показывает разброс количества бракованных деталей в ящиках. Мода показывает наиболее часто встречающееся количество бракованных деталей. Ответ: 1,7; 3; 4. 5. № 183. Решение: Среднее значение находим по формуле среднего арифметического: X =  = 0,9.Составим таблицу отклонений от средней температуры воздуха в полдень в каждый из дней декады:
Обращаем внимание, что сумма всех отклонений (вторая строка таблицы) равна нулю. Ответ: 0,9 °С; таблица отклонений. IV. Итоги урока. – Какие существуют средние статистические характеристики ряда? – Как найти среднее арифметическое ряда? – Что такое размах ряда? Что он характеризует? – Что такое мода ряда? Что она характеризует? Домашнее задание: № 178, № 182 Урок 22 Медиана упорядоченного ряда Цели: ввести понятие медианы как статистической характеристики упорядоченного ряда; формировать умение находить медиану для упорядоченных рядов с четным и нечетным числом членов; формировать умение интерпретировать значения медианы в зависимости от практической ситуации. Ход урока I. Устная работа. Даны ряды: 1) 4; 1; 8; 5; 1; 7. 2)  ; 9; 3; 0,5;  .3) 6; 0,2;  ; 4; 6; 7,3; 6.Найдите: а) наибольшее и наименьшее значения каждого ряда; б) размах каждого ряда; в) моду каждого ряда. II. Объяснение нового материала. Объяснение проводить согласно пункту 10 учебника. Следует подчеркнуть, что перед нахождением медианы нужно всегда упорядочить ряд данных. На доску следует вынести правила нахождения медианы для рядов с четным и нечетным числом членов:
Особое внимание следует уделить интерпретации значений медианы для различных задач. Учитель должен прививать критическое отношение к статистическим выводам и обобщениям. |
