Урок 1 Числовые выражения
 Скачать 2.02 Mb.
|
|
Домашнее задание: № 415; № 418; № 419 (б, г, е); № 420 (б, г); № 421 (в, г); № 422. Урок 43 Умножение и деление степеней Цель: формировать умение использовать правила умножения и деления степеней с одинаковыми основаниями при решении практических задач. Ход урока I. Проверочная работа. Вариант 1 1. Представьте в виде степени произведение. а) x6∙ x3∙ x7; б) (–7)3∙ (–7)2∙ (–7)9. 2. Представьте в виде степени частное. а) x8: x4; б) (–0,5)6 : (–0,5)8. 3. Найдите значение выражения. а)  ; б)  .Вариант 2 1. Представьте в виде степени произведение. а) y5∙ y9∙ y2; б) (–6)8∙ (–6)2∙ (–6)3. 2. Представьте в виде степени частное. а) z10 : z7; б)  .3. Найдите значение выражения. а)  ; б)  .II. Мотивация изучения. Данная тема предоставляет учителю возможность познакомить детей с числовыми величинами, которыми можно выразить количественные отношения реального мира. В этом плане особенно важны задачи, содержащие реальные величины, например задачи о Солнечной системе, планетах и других космических телах. Полезно ознакомить учащихся с названиями классов принятой десятичной нумерации:
Интересно для сравнения привести наименования классов старинной русской нумерации. Л. Магницкий в своей «Арифметике», изданной при Петре I, упоминает такие названия: 103 – тысяча 104 – тьма 105 – легион 106 – леодр 107 – вран 108 – колода. Операции с числовыми великанами делают актуальными приближенные вычисления. Если исходные данные в задаче получены в результате измерений (например, астрономических) с точностью до 2–3 десятичных знаков, нет никакого смысла в последующих десятках цифр. Поэтому в этой теме уместно познакомить детей с правилами округления чисел. III. Формирование умений и навыков. 1. Найдите отношение массы каждой из планет Солнечной системы к массе Земли. Справка.
2. В астрономии одной из единиц длины является световой год, то есть расстояние, которое проходит за год луч света. Скорость света с = 300 000 км/с. Вычислите: а) за какое время луч света доходит от Земли до Луны, от Солнца до Земли; б) величину светового года в километрах; в) расстояние от Земли до звезды Сириус в световых годах. Справка. Среднее расстояние от Земли до Луны 384 000 км, от Земли до звезды Сириус 8,2 · 1013 км. 3. Ежегодно прирост древесины на опытном участке составляет 10 %. Какое количество древесины будет на участке через 10 лет, если сейчас её 105 м3? 4. В сберегательном банке вкладчику начисляется 20 % в год от сданной на хранение суммы. Через сколько лет первоначальная сумма увеличится более чем в 2 раза; в 5 раз? 5. Найдите массу мотка медной проволоки сечением 2 мм и длиной 50 м. Справка. Масса вычисляется по формуле m = ρ ∙ V, где ρ – плотность вещества. В частности, для меди ρ = 8,9 г/см3. А для вычисления объема цилиндра V нужно воспользоваться формулой V = πR2H. 6*. Какое наибольшее число абонентов может быть прикреплено к одной АТС при семизначной записи номеров телефона? Первые три цифры всех номеров данной АТС одинаковы. IV. Итоги урока. – Сформулируйте определение степени с натуральным показателем. – В каких областях используются вычисления больших степеней числа 10? Домашнее задание: 1. Во сколько раз число 4,8 · 1019 больше числа 1,2 · 1019? 2. Найдите расстояние от Солнца до планет Солнечной системы в астрономических единицах. Справка.
Астрономическая единица (а. е.) – среднее расстояние от Солнца до Земли. 3. № 542; № 543. Вариант 1 1. Представьте в виде степени произведение. а) x6∙ x3∙ x7; б) (–7)3∙ (–7)2∙ (–7)9. 2. Представьте в виде степени частное. а) x8: x4; б) (–0,5)6 : (–0,5)8. 3. Найдите значение выражения.а) ; б) .Вариант 2 1. Представьте в виде степени произведение. а) y5∙ y9∙ y2; б) (–6)8∙ (–6)2∙ (–6)3. 2. Представьте в виде степени частное. а) z10 : z7; б) .3. Найдите значение выражения.а) ; б) .Вариант 1 1. Представьте в виде степени произведение. а) x6∙ x3∙ x7; б) (–7)3∙ (–7)2∙ (–7)9. 2. Представьте в виде степени частное. а) x8: x4; б) (–0,5)6 : (–0,5)8. 3. Найдите значение выражения.а) ; б) .Вариант 2 1. Представьте в виде степени произведение. а) y5∙ y9∙ y2; б) (–6)8∙ (–6)2∙ (–6)3. 2. Представьте в виде степени частное. а) z10 : z7; б) .3. Найдите значение выражения.а) ; б) .Вариант 1 1. Представьте в виде степени произведение. а) x6∙ x3∙ x7; б) (–7)3∙ (–7)2∙ (–7)9. 2. Представьте в виде степени частное. а) x8: x4; б) (–0,5)6 : (–0,5)8. 3. Найдите значение выражения.а) ; б) .Вариант 2 1. Представьте в виде степени произведение. а) y5∙ y9∙ y2; б) (–6)8∙ (–6)2∙ (–6)3. 2. Представьте в виде степени частное. а) z10 : z7; б) .3. Найдите значение выражения.а) ; б) .Вариант 1 1. Представьте в виде степени произведение. а) x6∙ x3∙ x7; б) (–7)3∙ (–7)2∙ (–7)9. 2. Представьте в виде степени частное. а) x8: x4; б) (–0,5)6 : (–0,5)8. 3. Найдите значение выражения.а) ; б) .Вариант 2 1. Представьте в виде степени произведение. а) y5∙ y9∙ y2; б) (–6)8∙ (–6)2∙ (–6)3. 2. Представьте в виде степени частное. а) z10 : z7; б) .3. Найдите значение выражения.а) ; б) .Урок 44 Возведение в степень произведения и степени Цели: вывести правило возведения в степень произведения двух и более сомножителей; формировать умение вычислять степень произведения, а также рационально преобразовывать выражения, содержащие степень произведения либо предполагающие использование данного свойства. Ход урока I. Организационный момент Устная работа. Вычислите. а) 23 · 53; в) 122; д) 53 ·  ; ж) (bx)5;б) 103; г) 32 · 42; е) (2а)3; з) (ab)n. II. Объяснение нового материала.
Доказательство: (ab)n = (ab) · (ab) · ... · (ab) по определению степени п раз; (ab) · (ab) · ... · (ab) = (aa...a)(bb...b) по свойствам умножения п раз п раз; (ab)n = anbn. Вывод: 1) каждый множитель возводить в эту степень; 2) результаты перемножить. Пример: (abсd)4 = ... Решение: (abcd)4 = a4b4c4d4. Рассмотреть пример 1 со с. 97 учебника. III. Формирование умений и навыков. 1. № 428. 2. Выполните возведение в степень, представив предварительно основание степени в виде произведения множителей –1 и х: а) (–х)2; б) (–х)8; в) (–х)100; г) (–х)2п; д) (–х)3; е) (–х)9; ж) (–х)71; з) (–х)2п + 1. Решение: а) (–х)2 = ((–1) · х)2 = (–1)2 · х2 = 1 · х2 = х2; е) (–х)9 = ((–1) · х)9 = (–1)9 · х9 = –1 · х9 = –х9; г) (–х)2п = ((–1) · х)2п = (–1)2п · х2п = 1 · х2п = х2п; з) (–х)2п + 1 = ((–1) · х)2п + 1 = (–1)2п + 1 · х2п + 1 = –1 · х2п + 1 = –х2п + 1. 3. № 431. Решение: а и –а – противоположные числа. а2; (–а)2 = ((–1) · а)2 = (–1)2 · а2 = 1 · а2 = а2, значит, а2 = (–а2). 4. № 432. Решение:
Аналогично рассуждаем для остальных случаев. 5. № 433. Решение:
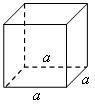
6. № 434. Для решения используем данные задачи № 432. Решение: Поверхность куба состоит из 6 квадратов площадью а2, то есть равна 6а2. Если ребро куба увеличить в 3 раза, то площадь боковой грани составит 9а2, а общая площадь поверхности равна 6 · 9а2 или 54а2. Новая площадь больше в 9 раз, значит, и краски потребуется в 9 раз больше, то есть 40 · 9 = 360 г. Следовательно, 350 г краски на хватит. Ответ: не хватит. 7. Представьте произведение в виде степени. а) x5y5; б) 36a2b2; в) 0,001x3c3; г) –х3; д) –8х3; е) –32a5b5; ж) x5y5z5; з) 0,027a3b3c3; и)  x3a3z3.8. Вычислите значение выражения, используя свойство степени произведения. а) 53 · 23; в) (0,5)3 · 603; б)  · 204; г) (1,2)4 ·  . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
