Урок 1 Числовые выражения

• Название: Урок 1 Числовые выражения
• Дата: 06.04.2022
• Размер: 2.02 Mb.
• Имя файла: 1-63.doc
• Тип: Урок; #448079
• страница: 2 из 26

Вариант 2

1. Заполните таблицу:

т	0	–1	3	2	–2
п	–2	–3	6	0	1
т (п – 2т)

2. Найдите значение выражения а – b + 3c, если а – b = 11 и с = –6.
Вариант 1

1. Заполните таблицу:

р	0	–1	2	–3	3
t	–7	–2	3	0	9
p (3t – p)

2. Найдите значение выражения х + у – 2z, если х + у = 3 и z = –2.

Вариант 2

1. Заполните таблицу:

т	0	–1	3	2	–2
п	–2	–3	6	0	1
т (п – 2т)

2. Найдите значение выражения а – b + 3c, если а – b = 11 и с = –6.

Вариант 1

1. Заполните таблицу:

р	0	–1	2	–3	3
t	–7	–2	3	0	9
p (3t – p)

2. Найдите значение выражения х + у – 2z, если х + у = 3 и z = –2.

Вариант 2

1. Заполните таблицу:

т	0	–1	3	2	–2
п	–2	–3	6	0	1
т (п – 2т)

2. Найдите значение выражения а – b + 3c, если а – b = 11 и с = –6.

Вариант 1

1. Заполните таблицу:

р	0	–1	2	–3	3
t	–7	–2	3	0	9
p (3t – p)

2. Найдите значение выражения х + у – 2z, если х + у = 3 и z = –2.

Урок №3 Выражения с переменными

Цели: продолжить формировать умение находить значение выражения с переменными; формировать умение составлять выражение с переменными по условию задачи, в том числе формулы, и находить их значение.

Ход урока

I. Устная работа.

1. Назовите выражения, не имеющие смысла.

а) 2 · 4 – 8; б) 3 · 2 : (6 – 1,5 · 4); в) ;

г) 3 : 3 – 7 · 2; д) ; е) ;

ж) 2 : 4 – 2; з) 3 : .

2. Найдите значение выражения 3а – b, если:

а) а = 2 и b = –4; б) а = 0 и b = ;

в) а = –4 и b = 5; г) а = – и b = .

3. Сколько процентов составляет:

а) 50 от 200; б) 13 от 260;

в) 1,5 от 20; г) 240 от 80?

II. Объяснение нового материала.

Вводится понятие формулы.Приведу примеры различных формул, применяемых на практике (вычисление площадей, объемов, числовые формулы и т. п.). Также следует объясняю что есть стабильные формулы, которые уже выведены и могут использоваться для расчетов. А есть задачи, для решения которых необходимо самостоятельно выявить закономерности (зависимости), описанные в условии, ввести переменные, составить выражение с переменными (формулу) и использовать его для вычисления искомого задачи при конкретных исходных данных.

III. Формирование умений и навыков.

1. № 29.

Решение:

Если площадь первого участка а га, а с каждого га собрали 32 ц пшеницы, то со всего участка собрали 32а ц пшеницы. Аналогично получаем для второго участка урожай 40b ц пшеницы. Тогда с обоих участков был собран урожай 32а + 40b (ц). Если а = 120 и b = 80, то 32а + + 40b = 32 · 120 + 40 · 80 = 3840 + 3200 = 7040.

Ответ: 32а + 40b (ц); 7040 ц.

2. № 31.

Решение:

Фигура состоит из отдельных частей. её площадь можно найти двумя способами:

1-й способ. «Разбить» фигуру на отдельные фигуры, для которых можно легко найти площадь, и, сложив полученные результаты, получить общую площадь.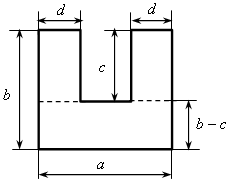



Площадь состоит из суммы площадей трех прямоугольников со сторонами: d и с; d и с; а и b – с. Их площади соответственно равны: сd; сd; а (b – с). Значит, площадь искомой фигуры составляет:

сd + сd + а (b – с) или 2сd + а (b – с).

2-й способ. Представить фигуру в виде прямоугольника со сторонами а и b с «вырезанным» прямоугольником со сторонами с и а – 2d. Их площади соответственно равны аb и с (а – 2d). Значит, площадь искомой фигуры составляет аb – с (а – 2d).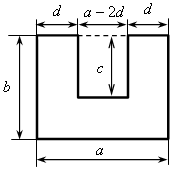



Ответ: 2сd + а (b – с) (см²) или аb – с (а – 2d) (см²).

3. № 33.

Решение:

После добавления 5 г соли в раствор масса его стала равна 255 г. Масса чистой соли в растворе также увеличилась на 5 г и стала составлять (х + 5) г. Концентрация соли, таким образом, составляет ∙ 100 %.

Ответ: ∙ 100 %.

4. № 35 (устно); № 36 (устно).

2-я группа

1. № 37 (устно); № 38.

2. № 39 (устно); № 40 (устно).

3. № 41 (устно); № 42.

iV. Проверочная работа.

Вариант 1

Составьте выражение для вычисления площади пола, уложенного п квадратными плитками со стороной а см. Вычислите эту площадь, если а = 20 и п = 500.

Вариант 2

Составьте выражение для вычисления пути, пройденного велосипедистом за время t ч со скоростью υкм/ч. Вычислите путь велосипедиста, если υ = 25, t = 1,2.

V. Итоги урока.

– Что называется значением выражения с переменными?

– В каком случае выражение с переменными не имеет смысла? Назовите выражение, которое содержит переменную х и которое не имеет смысла при х = –3,5.

– Назовите выражение, имеющее смысл при любых значениях входящей в него переменной у.

– Что представляет собой формула? Назовите формулу четного числа, нечетного числа.

Домашнее задание: 1. № 30, № 32, № 34, № 43.

Урок №4
Сравнение значений числовых выражений
и выражений с переменными

Цели: формировать умение сравнивать значения числовых выражений, а также буквенных выражений при заданных значениях входящих в них переменных; применять свойства действий над числами при нахождении значений числовых выражений; ввести понятие двойного неравенства; формировать умение записывать результат сравнения выражений в виде двойного неравенства.

Ход урока

I. Организационный момент

Устная работа.

1. Проанализируйте порядок выполнения действий в каждом из данных выражений и объясните, как оно читается:

а) а + b;
б) а · b;
в) 2аb;
г) а + (b – с);

д) ;
е) 2х – 3у;
ж) ak + p;
з) .

2. От куска проволоки длиной а м первый раз отрезали b м, а второй раз – с м проволоки. Какой смысл имеют следующие выражения:
а) b + с; б) а – (b + с); в) а – b; г) а – b – с?

3. Поставьте вместо звездочек такое число, чтобы получилось верное равенство.

а) –(–12) = *; б) 1,5 = –(*); в) = –8 = –(*); г) 0 = –(*).
II. Объяснение нового материала.

Рассмотрим задачу со с. 10 учебника. Она носит чисто практический характер, и её решение служит мотивацией изучения темы. Показываем учащимся, что при записи неравенства слева или справа (или в обеих частях) может стоять числовое выражение. Просим назвать неравенства.

Здесь следует напомнить, что неравенства бывают верные или неверные.

Задание. Определите, верно ли неравенство.

а) 3 · 15 > 8 : 2; б) 14 : 2 < –3 · 2;

в) 1,7 · 10 > 7 : 10; г) < –2,5 ∙ 2.

Показываем на конкретных примерах, что если выражения содержат переменные, то для разных значений переменных результат сравнения значений этих выражений может оказаться различным.

Рассматриваем пример со с. 10 учебника. Также целесообразно попросить учащихся подобрать несколько значений переменной а, при которых будут верны либо не верны неравенства 2а > а + 4 и 2а < а + 4.

Вводим понятие двойного неравенства. Обращаем внимание на различные формулировки прочтения двойного неравенства.

III. Формирование умений и навыков.

1. Сравните значение выражений:

а) и ; б) и ;

в) 0,5 и ; г) и –1,6;

д) 3,2 · 6,01 и 77,2 : 4; е) 38,4 : 6 и 12 – 5,6.

2. № 50.

3. № 48 (а; в); № 49 (а; б).

1. № 51; № 52 (устно).

2. Сравните значения выражений:

а) 2х + 5 при х = 0 и х = –1 ;

б) 3 – 3а при а = 1 и а = –1;

в) 3х + 5у при х = –0,3, у = 0,6 и х = 1,2, у = –0,3;

г) 7а + b – 2c при а = 2, b = –4, с = 3 и а = –1,2, b = 0,4, с = 1.

3. Для выражений 25х + 1 и 800 : х – 99 составьте таблицу значений при х = 1; 2; 4; 5; 8. При каких из этих значений х:

а) первое выражение меньше второго;

б) первое выражение равно второму;

в) первое выражение больше второго?

Решение:

х	1	2	4	5	8
25х + 1	26	51	101	126	201
800 : х – 99	701	301	101	61	1

Ответ: а) 1; 2; б) 4; в) 5; 8.

1. № 56, № 57.

2. Какие числа, кратные 5, удовлетворяют неравенству:

а) 64 < х < 78; б) 405 < у < 450?

3. Запишите все числа х, у которых знаменатель дробной части 10, если .

4. № 59.