Урок 1 Числовые выражения
 Скачать 2.02 Mb. Скачать 2.02 Mb.
|
|
III. Формирование умений и навыков. 1. № 484, № 485. 2. № 487. Решение: а) А (6; 36) 36 = 62; 36 = 36 – верно, значит, принадлежит; б) В (–1,5; 2,25) 2, 25 = (–1,5)2; 2,25 = 2,25 – верно, значит, принадлежит; в) С (4; –2) –2 = 42; –2 = 16 – неверно, значит, не принадлежит; г) D (1,2; 1,44) 1,44 = (1,2)2; 1,44 = 1,44 – верно, значит, принадлежит. Ответ: а) да; б) да; в) нет; г) да. 3. № 489. 4. № 490. Решение: а) А (–0,2; –0,008) –0,008 = (–0,2)3; –0,008 = –0,008 – верно, значит, принадлежит; б) B   ; ; ; ;в) C   ; ;Ответ: а) да; б) да; в) нет. 5. № 491. 6. № 492. Решение: а) Р (а; 64) 64 = а2; 82 = а2 – возможно в случае а = 8 или а = –8. б) Р (а; 64) 64 = а3; 43 = а3 возможно в случае а = 4. Ответ: а) 8; –8; б) 4. IV. Итоги урока. – Сформулируйте свойства функции y = x2. Как отражаются эти свойства на графике функции? – Как называется график функции y = x2? – Сформулируйте свойства графика функции y = x3. Как отражаются эти свойства на графике функции? – Как называется график функции y = x3? Домашнее задание: № 486; № 488; № 562; № 563. Урок 51 Функции y = x2 и у = х3 и их графики Цели: формировать понятие графического решения уравнения как нахождения абсциссы точек пересечения графиков двух функций; формировать умение решать графически уравнения вида у = х2 и у = х3. Ход урока I. Устная работа. 1. Заданы функции: 1) у = 2х; 4) у = 3х + 2; 7) у = 2) у = 3) у = –3х; 6) у = –3х – 2; 9) у = х3. На рисунках а) – и) изображены графики этих функций. Заполните таблицу соответствия:
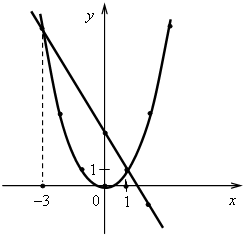
a) 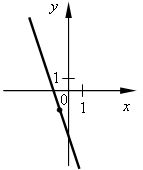 б) б) 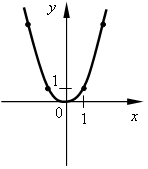 в) в) 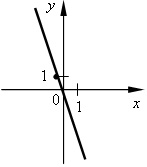 г) г) 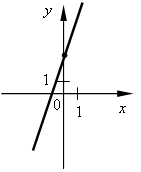 д) д) 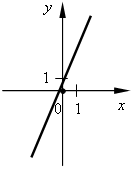 е) е) 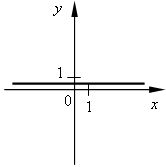 ж) ж) 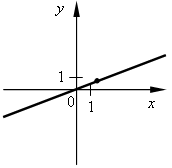 з) з) 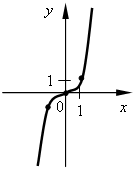 и) и) 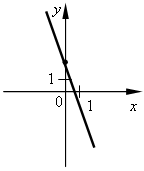 2. Как называется функция вида y = kx? 3. Как называется функция вида y = kx + b? 4. Как называется график функции y = x2? 5. Как называется график функции вида y = x3? II. Актуализация знаний. Решить уравнение. а) x2 = 16; б) x3 = 8; в) x2 = III. Объяснение нового материала. Необходимо разъяснить принцип графического решения уравнения. Рассматриваем примеры 1, 2 со с. 109 учебника. Показываем, что равенство (аналитическое) x2 = x + 1 можно понимать как равенство значений двух функций y = x2 и y = x + 1. Графически, если графики этих функций пересекаются, то точка пересечения показывает значение х (абсцисса), при котором значения функций (ордината) равны. алгоритм графического решения уравнения: 1-й шаг. Преобразовать уравнение к равенству двух функций известного вида (y = kx; y = kx + b; y = x2; y = x3). 2-й шаг. В одной системе координат построить графики этих функций. 3-й шаг. Определить наличие или отсутствие точки (точек) пересечения. 4-й шаг. Если точки пересечения есть, то найти по графику их абсциссы, которые и будут являться решениями уравнения. Если точек пересечения нет, то, значит, уравнение не имеет решений. Проверить полученное значение можно, подставив в уравнение. IV. Формирование умений и навыков. 1. № 493 (устно). 2. Решите графически уравнение. а) x2 = 2x; б) x2 = 3. № 566. В следующем упражнении от учащихся требуется сначала преобразовать уравнение к «удобному» виду, а затем решить его графически.
V. Итоги урока. – В каком случае уравнение можно решить графически? – Назовите алгоритм решения уравнения графическим способом. – В каком случае уравнение не имеет корней? – Как можно проверить точность корней уравнения, найденных графическим способом? Домашнее задание: 1. Решите графически уравнение. а) х = 3х; б) 2x = 2. Решите графически уравнение. а) x2 = 9; б) x2 = 3. Решите уравнение графически. а) x2 = 6 – x; б) x2 + 4x = –3; в) x2 – 4x = 0; г) x3 + 2 = 3x. Урок 52 Функции y = x2 и у = х3 и их графики Цели: обобщить и систематизировать знания по теме «Степень с натуральным показателем»; оценить степень сформированности умений и навыков, провести коррекционную работу. Ход урока I. Устная работа. 1. Представьте в виде степени. а) c7 ∙ c4; б) b ∙ b2 ∙ b3; в) (–7)3 ∙ (–7)8 ∙ (–7)9; г) a10 : a8; д) 214 : 29; е) (x5)2; ж) (–a3)3; з)  ; и) (a2)5 ∙ a5. ; и) (a2)5 ∙ a5.2. Упростите. а) (a5)2 ∙ (a2 ∙ a3)2; в) (4xy)2; д) 94 : 37; б) (y4)5 : (y4)2; г) 20a3 ∙ (5a)2; е) 1012 : (24 ∙ 54). 3. Выполняя задания, ученик допустил ошибки. Какие свойства, правила не знает ученик? 35 ∙ 38 = 340; 81 = 1; 24 + 22 = 26; (2a)5 = 2a5; (x2)3 = x8. 4. Представьте в виде степени. (–3)8 ∙ (–3)4; (0,1)20 : (0,1)6; (xn)2. 5. Найдите значение выражения. (1014 ∙ 107) : 1019; 53 ∙ 23. 6. Представьте произведение в виде степени. x5y5; 36a2b2; II. Теоретический опрос. 1) Сформулируйте определение степени с натуральным показателем. 2) Каким числом является: а) степень положительного числа; б) степень отрицательного числа с четным показателем; в) степень отрицательного числа с нечетным показателем? 3) Сформулируйте правило умножения степеней с одинаковыми показателями. 4) Сформулируйте правило деления степеней с одинаковыми показателями. 5) Дайте определение степени числа с нулевым показателем. 6) Сформулируйте правило возведения степени в степень. 7) Сформулируйте правило возведения в степень произведения. III. Математический диктант. Вариант 1 1. Упростите. а) x2 ∙ x8 : x; б) a10 : a6 ∙ a4. 2. Найдите значение выражения. 94 : 37. 3. Представьте в виде квадрата одночлена. 0,25х4; 49т2п6. 4. Выполните умножение. 5. Вычислите. (516 · 316) : 1515. Вариант 2 1. Упростите. а) b3 ∙ b7 : b; б) y12 : y5 ∙ y2. 2. Найдите значение выражения. 44 : 26. 3. Представьте в виде квадрата одночлена. 0,36у6; 100с2а6. 4. Выполните умножение. 5. Вычислите. (310 · 710) : 219. IV. Работа по карточкам. Карточка № 1 1. Вычислите. (494 · 75) : 712. 2. Упростите выражения. а)  ; б) am + 1 · a · a3 – m. ; б) am + 1 · a · a3 – m.Карточка № 2 1. Вычислите. (56 · 125) : 254. 2. Упростите выражения. а)  ; б) x2n : (xn – 1)2. ; б) x2n : (xn – 1)2.V. Итоги урока. Домашнее задание: 1. Повторить п. 18–23. 2. Ответьте на вопросы теста: 1) Выполните умножение: 0,5х2у · (–ху) = а) –0,5х3у2; б) 0,5у2х3; в) –0,5х2у3. 2) Упростите: –0,4x4y3 · 2,5x2y7 = а) x8y6; б) –10x6y7; в) –x6y7. 3) Преобразуйте выражение в одночлен стандартного вида: 20а3 · (–5а)2 = а) 100а5; б) –500а6; в) 500а5. 4) Вычислите: (25 · (23)4) : 213 = а) 23; б) 16; в) 32. 1. Представьте в виде степени. а) c7 ∙ c4; б) b ∙ b2 ∙ b3; в) (–7)3 ∙ (–7)8 ∙ (–7)9;г) a10 : a8; д) 214 : 29; е) (x5)2; ж) (–a3)3;з) 2. Упростите. а) (a5)2 ∙ (a2 ∙ a3)2; в) (4xy)2; д) 94 : 37; б) (y4)5 : (y4)2; г) 20a3 ∙ (5a)2; е) 1012 : (24 ∙ 54). 3. Выполняя задания, ученик допустил ошибки. Какие свойства, правила не знает ученик? 35 ∙ 38 = 340; 81 = 1; 24 + 22 = 26; (2a)5 = 2a5; (x2)3 = x8. 4. Представьте в виде степени. (–3)8 ∙ (–3)4; (0,1)20 : (0,1)6; (xn)2. 5. Найдите значение выражения. (1014 ∙ 107) : 1019; 53 ∙ 23. 6. Представьте произведение в виде степени. x5y5; 36a2b2; |