Поурочные разработки по геометрии 10 класс Атанасян (1). Урок 1 предмет стереометрии. Аксиомы стереометрии цель рассмотреть основные свойства плоскости
 Скачать 1.97 Mb.
|
|
Ход урока I. Проверка домашнего задания (№№ 243, 244). II. Устная работа.
2. Основание пирамиды – прямоугольник, одно боковое ребро перпендикулярно основанию пирамиды. Определить вид боковых граней.
III. Объяснение нового материала (п. 29) IV. Решение задач: №№ 254, 255, 257. Домашнее задание: теория (п. 33), №№ 256, 258, 259. Контрольные вопросы Продолжите предложения. 1. У правильной пирамиды: а) боковые ребра… б) боковые грани… в) апофемы… г) двугранные углы при основании… д) двугранные углы при боковых ребрах… 2. Каждая точка высоты правильной пирамиды равноудалена от всех _________________ основания. 3. Каждая точка высоты правильной пирамиды равноудалена от всех _________________ граней. 4. Боковыми гранями правильной пирамиды являются… 5. Площадь боковой поверхности правильной пирамиды равна произведению полупериметра основания на… Урок 7 ПИРАМИДА. ПРАВИЛЬНАЯ ПИРАМИДА Цель: сформировать навык решения задач по изученной теме. Ход урока I. Проверка домашнего задания. II. Устная работа. 1. Как в правильной пирамиде найти точку, равноудаленную от всех вершин? 2. Как в правильной пирамиде найти точку, равноудаленную от всех ее граней?
III. Решение задач: №№ 261, 262, 264, 266. Домашнее задание: теория (п. 29), №№ 260, 263, 265. Контрольные вопросы Выберите верный ответ из числа предложенных. 1. Чему равна высота правильной треугольной пирамиды со стороной основания а и боковым ребром b? а) h =  ; б) h = ; в) h = .2. Чему равна сторона основания правильной шестиугольной пирамиды, если её высота h и боковое ребро b? а) a =  ; б) a = ; в) a = .3. Чему равна высота правильной шестиугольной пирамиды со стороной основания а и боковым ребром b? а) h =  ; б) h = ; в) h = .4. Чему равна апофема правильной четырехугольной пирамиды со стороной основания а и высотой h? а) l =  ; б) l = ; в) l = .5. Чему равна апофема правильной треугольной пирамиды со стороной а и боковым ребром b? а) l = ; б) l = ; в) l = .6. Чему равна апофема правильной шестиугольной пирамиды со стороной а и высотой h? а) l =  ; б) l = ; в) l = .7. Чему равна площадь полной поверхности правильной пирамиды? а) S = Ph + Sосн; б) S =  + Sосн; в) S = Pl + Sосн, где h – высота пирамиды, l – апофема, P – периметр основания.8. Имеет ли правильная четырехугольная пирамида ось симметрии? а) да; б) нет. 9. Сколько плоскостей симметрии имеет: – правильная четырехугольная пирамида? а) 2; б) 3; в) 4. – правильный тетраэдр? а) 1; б) 3; в) не имеет. 10. Дана правильная треугольная пирамида. Верно ли, что ее апофемы равны? а) да; б) нет. Урок 8 ПИРАМИДА. КЛЮЧЕВЫЕ ЗАДАЧИ Цель: рассмотреть свойства пирамид, имеющих равные боковые ребра; равные апофемы. Ход урока I. Объяснение нового материала. 1. Вершина пирамиды проецируется в центр описанной около основания окружности, если: а) боковые ребра пирамиды равны; б) боковые ребра составляют с плоскостью основания равные углы; в) боковые ребра составляют с высотой пирамиды равные углы. Доказать. Составить обратные задачи. Доказать. 2. Вершина пирамиды проецируется в центр вписанной в основание окружности, если: а) апофемы равны; б) двугранные углы при ребрах основания равны; в) апофемы составляют с высотой пирамиды равные углы. Доказать. Составить обратные задачи. Доказать. II. Решение задач: №№ 246, 248, 250, 251. Домашнее задание: теория (знать ключевые задачи), №№ 247, 249, 252. Контрольные вопросы 1. Боковые ребра пирамиды равны между собой. Может ли основание пирамиды быть: 1) ромбом; 2) прямоугольником; 3) правильным шестиугольником? 2. Боковые ребра пирамиды равны между собой. Как расположена проекция вершины пирамиды на основании, если основание: 1) прямоугольник; 2) прямоугольный треугольник? 3. Двугранные углы при основании пирамиды равны между собой. Может ли в основании пирамиды быть: 1) равнобедренный треугольник; 2) ромб; 3) прямоугольник? 4. Вершина пирамиды проектируется в точку пересечения диагоналей основания. Что можно сказать о двугранных углах при основании пирамиды, если основание: 1) параллелограмм; 2) ромб; 3) равнобедренная трапеция? Урок 9 УСЕЧЕННАЯ ПИРАМИДА Цель: ввести понятие усеченной пирамиды. Ход урока I. Проверка домашнего задания (№ 252). II. Устная работа.
III. Объяснение нового материала построить в соответствии с пунктом 34 учебника. Обязательно решить в классе задачу № 267. Дополнительно доказать, что сечение – многоугольник, подобный основанию, и площади сечения и основания относятся как квадраты их расстояний от вершины. № 267. Если пирамида пересечена плоскостью, параллельной основанию, то: 1) боковые ребра и высота пирамиды делятся этой плоскостью на пропорциональные части; 2) сечение – многоугольник, подобный основанию; 3) площади сечения и основания относятся как квадраты их расстояний от вершины.
Доказательство 1) A1B1С1D1E1 || ABCDE, поэтому A1B1 || АВ, B1С1 || BC, С1D1 || СD, ..., А1О1 || АО (§ 34, теорема 2). Следовательно,  ;  ; …;  .В каждой из этих пропорций имеются попарно одинаковые отношения, и потому  .2) Δ А1SB1 Δ ASB, Δ B1SC1 Δ BSC, следовательно,  ,  , откуда .Аналогично получим:  и  , откуда  и т. д.Продолжая брать пары подобных треугольников, получим:  ...,то есть стороны сечения пропорциональны сторонам основания. Кроме того, стороны одноименных углов взаимно параллельны, и потому эти углы соответственно равны; следовательно, по определению подобных многоугольников A1B1С1D1E1 ABCDE. 3) A1B1С1D1E1 ABCDE, следовательно,  .Но Δ А1SО1 Δ ASО и Δ А1SВ1 Δ АSВ, поэтому  и  , откуда  .Из (1) и (2) следует, что  .Следствие. Площадь сечения, параллельного основанию пирамиды, – квадратная функция расстояния его плоскости от вершины (или основания) пирамиды. Пусть SO = h, SO1 = х, тогда  и  ;Sосн и h для данной пирамиды величины постоянные, обозначим  , тогда Sсеч = kx2, то есть площадь сечения – квадратная функция от х, где х – расстояние плоскости сечения от вершины пирамиды.Задача. В пирамиде сечение, параллельное основанию, делит высоту в отношении 2 : 3 (от вершины к основанию). Найти площадь сечения, зная, что оно меньше площади основания на 84 см2.
2) Sсеч = х; Sосн = х + 84, тогда из 1)  ;  ;  ; 25x = 4 (x + 84); 21x = 4 ∙ 84; x = 4 ∙ 4 = 16.Ответ: Sсеч = 16 см2. IV. Решение задач: № 268. Домашнее задание: теория (п. 34), №№ 269, 270. Урок 10 УСЕЧЕННАЯ ПИРАМИДА Цель: сформировать навык решения задач на усеченную пирамиду. Ход урока I. Проверка домашнего задания (№№ 269, 270). II. Устная работа. 1. Сравните изображения многогранников. Выделите признаки, характерные для усеченной пирамиды. Какой из этих многогранников не является усеченной пирамидой?  Как проверить, изображена ли усеченная пирамида?  Какие из следующих многогранников являются усеченными пирамидами? 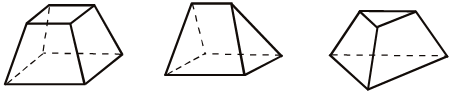 призматоида 2. Как построить усеченную пирамиду? 3. В пирамиде проведено сечение параллельно основанию через середину высоты. Площадь основания равна Q. Найдите площадь сечения. 4. В тетраэдре через середины трех ребер проведено сечение плоскостью. Что можно сказать о расстоянии вершин тетраэдра до плоскости сечения? 5. Продолжите предложения: а) основания усеченной пирамиды – …; б) перпендикуляр, проведенный из любой точки одного основания усеченной пирамиды на плоскость другого, называется…; в) в усеченной пирамиде боковые грани – …; г) боковые грани правильной усеченной пирамиды…; д) высота боковой грани усеченной пирамиды называется… III. Решение задач. 1. В пирамиде сечение, параллельное основанию, делит высоту в отношении 3 : 4 (от вершины к основанию), а площадь сечения меньше площади основания на 200 см2. Найти площадь основания. 2. На каком расстоянии от вершины пирамиды с высотой h надо провести сечение параллельно основанию, чтобы площадь сечения равнялась: 1) половине площади основания; 2)  ; 3)  площади основания.3. Высота правильной четырехугольной усеченной пирамиды равна 7 см, стороны оснований 10 см и 2 см. Найти боковое ребро пирамиды и диагональ. 4. Стороны оснований правильной треугольной усеченной пирамиды 4 дм и 1 дм, боковое ребро 2 дм. Найти высоту и апофему пирамиды. 5. Найти высоту правильных усеченных пирамид: 1) треугольной; 2) четырехугольной; 3) шестиугольной. Даны стороны а и b нижнего и верхнего оснований и угол α наклона бокового ребра к большему основанию. 6. 1) В правильной усеченной четырехугольной пирамиде стороны оснований равны а и b (а > b), двугранный угол при большем основании α. Найти высоту пирамиды. 2) То же, если пирамида треугольная. 7. 1) Высота правильной четырехугольной усеченной пирамиды равна 4 см, стороны оснований 2 см и 8 см. Найти площадь диагонального сечения. 2) Высота правильной четырехугольной усеченной пирамиды равна 4 см, диагональ 5 см. Найти площадь диагонального сечения. 8. В правильной усеченной треугольной пирамиде сторона большего основания а, сторона меньшего b, боковое ребро образует с основанием острый угол α.1) Провести сечение через боковое ребро и центр нижнего основания; 2) найти его площадь. 9. В правильной четырехугольной усеченной пирамиде стороны основания равны 3 см и 5 см, высота 3 см. Провести сечение через противолежащие стороны оснований. Найти: 1) площадь сечения; 2) двугранный угол между сечением и нижним основанием. Домашнее задание: теория (п. 34), №№ 313, 314. Урок 11 СИММЕТРИЯ В ПРОСТРАНСТВЕ. ПОНЯТИЕ ПРАВИЛЬНОГО МНОГОГРАННИКА. ЭЛЕМЕНТЫ СИММЕТРИИ ПРАВИЛЬНЫХ МНОГОГРАННИКОВ Цель: ввести понятие правильного многогранника. Ход урока I. Объяснение нового материала. О симметрии в пространстве учащиеся могут прочитать самостоятельно (п. 35). Далее ввести понятие правильного многогранника. (Рассматривая куб, правильный тетраэдр, правильный октаэдр и т. д., учащиеся отвечают на вопрос: по каким признакам можно объединить данные многогранники?) Установить вместе с учащимися, сколько может быть видов правильных многогранников? Пусть при одной вершине сходится n ребер, тогда плоских углов при этой вершине будет тоже n, причем они все равны между собой. Пусть один из этих плоских углов равен х, тогда сумма плоских углов при вершине nx, и по свойству плоских углов многогранного угла получим nx < 360°, откуда x <  (1).Угол правильного n-угольника равен α =  (2).
Начиная с n = 7 плоский угол станет меньше 60°, а такого правильного многоугольника не существует, поэтому остальные случаи рассматривать не будем. I. Грани правильного многогранника – правильные треугольники, тогда α = 60° (таблица II). 1) 60° ∙ 3 = 180° < 360°. В этом случае правильный многогранник имеет 4 грани и называется правильным тетраэдром. 2) 60° ∙ 4 = 240° < 360°. В этом случае правильный многогранник имеет 8 граней и называется правильным октаэдром. 3) 60° ∙ 5 = 300° < 360°. В этом случае правильный многогранник имеет 20 граней и называется правильным икосаэдром. 4) 60° ∙ 6 = 360°, это противоречит теореме о сумме плоских углов многогранного угла. Следовательно, больше правильных многогранников, грани которых – правильные треугольники, не существует. II. Грани правильного многогранника – правильные четырехугольники (квадраты), тогда α = 90° (таблица II). 1) 90° ∙ 3 = 270° < 360°. В этом случае правильный многогранник имеет 6 граней и называется правильным гексаэдром (кубом). 2) 90° ∙ 4 = 360°, следовательно, больше правильных многогранников, грани которых – квадраты, не существует. III. Грани правильного многогранника – правильные пятиугольники; α = 108°. 1) 108° ∙ 3 = 324° < 360°. В этом случае правильный многогранник имеет 12 граней, и называется правильным додекаэдром. 2) 108° ∙ 4 > 360°, следовательно, больше правильных многогранников, грани которых – правильные пятиугольники, не существует. IV. Начиная с правильного шестиугольника α ≥ 120° (таблица II). Следовательно, nα > 360° (n ≥ 3), поэтому правильных многогранников, грани которых – многоугольники с числом сторон больше 5, не существует. Во время беседы демонстрировать модели правильных многогранников, показывать рисунки (есть в параграфе). Последний пункт объяснения нового материала – элементы симметрии правильных многогранников. II. Решение задач: №№ 279, 280, 281, 282, 287. Домашнее задание: теория (п. 35–37), №№ 283, 285, 286. Урок 12 ПОДГОТОВКА К КОНТРОЛЬНОЙ РАБОТЕ Ход урока Вариант I 1. В основании прямого параллелепипеда ABCDA1B1C1D1 лежит ромб ABCD со стороной а, и углом BAD, равным 60°. Плоскость ВС1D составляет с плоскостью основания угол 60°. Найдите площадь полной поверхности параллелепипеда. 2. В основании пирамиды DABC лежит прямоугольный треугольник АВС,  С = 90°, А = 30°, ВС = 10. Боковые ребра пирамиды равно наклонены к плоскости основания. Высота пирамиды равна 5. Найдите площадь боковой поверхности пирамиды.3*. В указанной выше пирамиде найдите угол между прямыми АС и BD. Вариант II 1. Основанием прямого параллелепипеда служит параллелограмм со сторонами 3 см и 5 см. Острый угол параллелограмма равен 60°. Площадь большего диагонального сечения равна 63 см2. Найдите площадь полной поверхности параллелепипеда. 2. Основанием пирамиды MABCD служит ромб ABCD, АС = 8; BD = 6. Высота пирамиды равна 1. Все двугранные углы при основании равны. Найдите площадь полной поверхности пирамиды. 3*. В указанной выше пирамиде найдите угол между гранями ВМС и DMC. Вариант III 1. В основании прямого параллелепипеда ABCDA1B1C1D1 лежит параллелограмм ABCD, у которого BD  АВ; AB = 3 см; BD = 4 см. Плоскость АВ1С1 составляет с плоскостью основания угол 45°. Найдите площадь полной поверхности параллелепипеда.2. В основании пирамиды MABCD лежит квадрат ABCD со стороной, равной 12. Грани МВА и МВС перпендикулярны к плоскости основания. Высота пирамиды равна 5. Найдите площадь полной поверхности пирамиды. 3*. В указанной выше пирамиде найдите расстояние между прямыми ВС и MD. Вариант IV 1. В прямом параллелепипеде ABCDA1B1C1D1 основанием служит параллелограмм ABCD, AD = 2, DC = 2  , А = 30°. Большая диагональ составляет с плоскостью основания угол 45°. Найдите площадь боковой поверхности параллелепипеда.2. Основанием пирамиды МАВС служит прямоугольный треугольник АВС, катеты которого АС = 8 см, ВС = 6 см. Высота пирамиды равна 3  см. Двугранные углы при основании пирамиды равны между собой. Найдите площадь полной поверхности пирамиды.3*. В указанном выше параллелепипеде найдите угол между А1С и плоскостью грани DD1C1C. Домашняя контрольная работа Вариант I 1. Сторона основания правильной четырехугольной призмы ABCDA1B1C1D1 равна 4 см, а боковое ребро – 5 см. Найдите площадь сечения, которое проходит через ребро АА1 и вершину С. 2. В правильной треугольной призме сторона основания равна 3 см, а диагональ боковой грани составляет с плоскостью основания угол 60°. Площадь боковой поверхности призмы равна… 3. В наклонном параллелепипеде основанием служит квадрат. Две противоположные боковые грани перпендикулярны к плоскости основания. Все ребра параллелепипеда равны 4 см. Найдите площадь каждой из наклонных боковых граней. 4. В наклонной треугольной призме ABCA1B1C1 основанием служит правильный треугольник со стороной, равной а. Боковое ребро равно b, А1АС = А1АВ. Площадь грани СС1В1В равна…5. В наклонной треугольной призме боковое ребро равно 10 см. Площади двух боковых граней равны 30 см2 и 40 см2, угол между ними прямой. Площадь боковой поверхности призмы равна… 6. В правильной четырехугольной пирамиде угол между диагональю основания и скрещивающимся с ней боковым ребром равен… 7. В правильной четырехугольной пирамиде угол между противоположными боковыми гранями равен 40°. Найдите угол наклона боковых граней к плоскости основания. 8. Основанием пирамиды служит треугольник со стороной, равной 8 см, и противолежащим углом 150°. Боковые ребра наклонены к основанию под углом 45°. Высота пирамиды равна… 9. Основанием пирамиды служит трапеция, основания которой равны 2 см и 8 см. Боковые грани пирамиды равно наклонены к плоскости основания. Высота одной из боковых граней равна 10 см. Найдите площадь боковой поверхности пирамиды. 10. В пирамиде MABCD основанием служит квадрат со стороной, равной а. Грань МАВ – правильный треугольник, плоскость которого перпендикулярна к плоскости основания. Площади граней MAD и МВС равны… Вариант II 1. Сторона основания правильной четырехугольной призмы ABCDA1B1C1D1 равна 3 см, а боковое ребро – 4 см. Найдите площадь сечения, которое проходит через сторону основания АD и вершину С1. 2. В правильной треугольной призме боковое ребро равно 4 см, а диагональ боковой грани составляет с плоскостью основания угол 45°. Площадь боковой поверхности призмы равна… 3. В наклонном параллелепипеде основанием служит квадрат. Две противоположные боковые грани перпендикулярны к плоскости основания. Все ребра параллелепипеда равны между собой. Площадь наклонной боковой грани равна 25 см2. Длина ребра параллелепипеда равна… 4. Основанием наклонного параллелепипеда ABCDA1B1C1D1 служит квадрат со стороной, равной а. Боковое ребро равно b. Вершина А1 равноудалена от всех вершин нижнего основания. Площадь диагонального сечения ВВ1D1D равна… 5. В наклонной треугольной призме боковое ребро равно 5 см. Площади двух боковых граней равны 20 см2, угол между ними – 60°. Площадь боковой поверхности призмы равна… 6. В правильной треугольной пирамиде угол между скрещивающимися ребрами равен… 7. В правильной четырехугольной пирамиде боковые грани наклонены к основанию под углом 50°. Угол между противоположными боковыми гранями пирамиды равен… 8. В пирамиде основанием служит треугольник со стороной 6 см и противолежащим углом 30°. Боковые ребра наклонены к основанию под углом 60°. Длина бокового ребра равна… 9. Основанием пирамиды служит трапеция, боковые стороны которой равны 2 см и 4 см. Боковые грани пирамиды равно наклонены к плоскости основания. Высота одной из боковых граней равна 5 см. Найдите площадь боковой поверхности пирамиды. 10. В пирамиде MABCD основанием служит квадрат со стороной, равной 6 см. Ребро МВ перпендикулярно к плоскости основания. Равные боковые ребра равны 8 см. Площадь наклонных боковых граней равна… Урок 13 КОНТРОЛЬНАЯ РАБОТА № 4 Вариант I 1. Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площадь боковой поверхности пирамиды. 2. Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб ABCD, сторона которого равна а и угол равен 60°. Плоскость AD1C1 составляет с плоскостью основания угол в 60°. Найдите: а) высоту ромба; б) высоту параллелепипеда; в) площадь боковой поверхности параллелепипеда; г) площадь поверхности параллелепипеда. Вариант II 1. Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды. 2. Основанием прямого параллелепипеда ABCDA1B1C1D1 является параллелограмм ABCD, стороны которого равны а  и 2а, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:а) меньшую высоту параллелограмма; б) угол между плоскостью АВС1 и плоскостью основания; в) площадь боковой поверхности параллелепипеда; г) площадь поверхности параллелепипеда. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
SK = Н.
АВ, АО = ОВ,
.
, 
