Поурочные разработки по геометрии 10 класс Атанасян (1). Урок 1 предмет стереометрии. Аксиомы стереометрии цель рассмотреть основные свойства плоскости
 Скачать 1.97 Mb.
|
|
ГЛАВА 3. МНОГОГРАННИКИ 12 ЧАСОВ Урок 1 ПОНЯТИЕ МНОГОГРАННИКА. ПРИЗМА Цель: ввести понятия многогранника, призмы и их элементов. Ход урока I. Объяснение нового материала построить в соответствии с пунктом 30. При разговоре с учащимися использовать как можно больше моделей. Следует отметить, что в школьном курсе геометрии изучаются только простейшие выпуклые многогранники – выпуклые призмы и пирамиды, правильные многогранники. О полуправильных выпуклых многогранниках (изогонах, изоэдрах), выпуклых многогранниках, играющих большую роль в кристаллографии (параллелоэдрах), невыпуклых многогранниках (телах Пуансо) учащимся можно лишь сообщить, показывая модели, репродукции. Для закрепления понятий элементов многогранников следует с учащимися заполнить таблицу, раздав на каждую парту по модели.
В – число вершин многогранника, Р – число ребер многогранника, Г – число граней многогранника. В школе изучаются многогранники, Эйлерова характеристика которых равна 2. Это равенство верно для произвольного выпуклого многогранника (доказано Л. Эйлером в 1752 г.). Такого рода многогранники получили название многогранников нулевого рода. Учащиеся на опыте убедились, что у тетраэдра число вершин и число граней одинаково. Интересно выяснить, существуют ли еще такие многогранники. Контрольные вопросы 1. Объясните, что такое: а) многогранник; б) поверхность многогранника. 2. Какой многогранник называется выпуклым? 3. Куб – выпуклый многогранник (проверьте). Как, имея пилу, получить из деревянного куба модель невыпуклого многогранника? 4. Дан выпуклый многогранник. Что называют: а) его гранью; б) его ребром; в) его вершиной? 5. Назовите известные вам многогранники. а) Выпуклым или невыпуклым является каждый из них? б) Сколько граней, ребер и вершин у каждого? 6. Приведите пример многогранника, все грани которого: а) треугольники (кроме тетраэдра); б) квадраты (кроме куба); в) прямоугольники (кроме прямоугольного параллелепипеда). 7. Дан квадрат. На нем как на основании по разные стороны построены куб и пирамида. Сколько вершин, ребер и граней в полученном многограннике? 8. Два тетраэдра имеют общую грань и расположены по разные стороны от нее. Сколько вершин, ребер и граней имеет полученный многогранник? 9. Сколько трехгранных, двугранных и плоских углов: а) у тетраэдра; б) у параллелепипеда? Дополнительная литература: 1. Смирнова И. М. В мире многогранников. – М.: Просвещение, 1995 г. 2. Савченко В. Полуправильные многогранники // Квант, 1976, № 1. 3. Гамаюнов В. Модели звездчатых многогранников // Квант, 1981, № 2. Призма определяется как многогранник, обладающий определенными свойствами. На этом уроке достаточно ввести понятие призмы, ее элементов (п. 30). II. Решение задач: №№ 219, 223. Домашнее задание: теория (п. 27, 30). №№ 220, 295. Урок 2 ПРИЗМА. ПЛОЩАДЬ ПОВЕРХНОСТИ ПРИЗМЫ Цели: рассмотреть виды призм, ввести понятие площади поверхности призмы; вывести формулу для вычисления площади поверхности прямой призмы. Ход урока I. Проверка домашнего задания (№№ 219, 223) II. Устная работа. 1. Среди изображенных тел выберите те, которые являются призмами.  1 2 3 4 5 6 2. Назовите для призмы:
3. Закончите предложения. 1) Высотой призмы называется… 2) Диагональю призмы называется… 3) Диагональным сечением призмы называется сечение плоскостью, проходящей через… 4) Параллелепипедом называется… 5) Прямоугольным параллелепипедом называется… 6) Кубом называется прямоугольный параллелепипед, у которого… 7) Примеры моделей призмы и параллелепипеда из реальной жизни:.. 4. Ответьте на вопросы: 1) Какие многоугольники лежат в основании призмы? 2) В каких плоскостях лежат основания призмы? 3) Какими отрезками являются боковые ребра призмы? 4) Какими фигурами являются боковые грани призмы? 5) Что представляет собой диагональное сечение призмы? 6) Какими фигурами являются все грани параллелепипеда? 7) Какими фигурами являются все грани прямоугольного параллелепипеда? 8) Сколько измерений у прямоугольного параллелепипеда? 9) Почему все высоты призмы равны между собой? 10) Какие многоугольники являются основанием и боковой гранью пятиугольной призмы? 11) Призма имеет 30 граней. Какой многоугольник лежит в ее основании? Сколько вершин и ребер имеет эта призма? 12) Сколько диагоналей можно провести в четырехугольной призме? III. Объяснение нового материала. Виды призм   Устно № 218. Далее ввести понятие боковой поверхности, полной поверхности прямой призмы (п. 30). Можно использовать развертки призм. 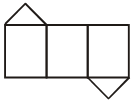 IV. Решение задач: №№ 221, 222, 225, 230. Домашнее задание: теория (п. 30), №№ 224, 229, 231. Урок 3 ПРИЗМА. НАКЛОННАЯ ПРИЗМА Цель: вывести формулу для вычисления боковой поверхности наклонной призмы, сформировать навык ее использования при решении задач. Ход урока I. Проверка домашнего задания. II. Устная работа. 1. Продолжите предложения. 1) Призма называется наклонной, если… 2) Призма является прямой, если… 3) Призма называется правильной, если… 4) Боковой поверхностью призмы называется… 5) Площадью полной поверхности призмы называется сумма… 6) Площадь боковой поверхности прямой призмы равна произведению… 7) Все двугранные углы при боковых гранях прямой призмы… 8) Правильная четырехугольная призма, высота которой равна стороне основания, является… 2. Ответьте на вопросы. 1) В какой призме боковые ребра параллельны ее высоте? 2) Если все ребра призмы равны, то будет ли она правильной? Ответ поясните. 3) Существует ли призма, у которой только одна боковая грань перпендикулярна основанию? Ответ поясните. 4) Может ли диагональ прямоугольного параллелепипеда быть меньше: а) бокового ребра? б) стороны основания? в) диагонали боковой грани? 5) Дан наклонный параллелепипед. Известно, что угол основания равен 150°. Какое из диагональных сечений параллелепипеда больше? 6) Будет ли сечение, перпендикулярное боковому ребру призмы, перпендикулярно к ее боковой грани? Ответ обоснуйте. 3. Выберите верный ответ из числа предложенных. 1) Чему равна площадь боковой поверхности куба с ребром 10 см? а) 40 см2; б) 400 см2; в) 100 см2; г) 400 см. 2) Чему равна площадь полной поверхности куба с ребром 6 см? а) 36 см2; б) 144 см2; в) 216 см2; г) 144 см. 3) Чему равна площадь боковой поверхности правильной четырехугольной призмы, если её высота h, сторона основания а? а) ha; б) 4ah; в) 42h; г) 4(a + h). 4) Чему равна площадь полной поверхности куба, если его диагональ равна d ? а) 2d 2; б) 6d 2; в) 3d 2; г) 4d 2.. 5) Прямоугольный параллелепипед имеет три измерения, равные а = 5 см; b = 8 см; h = 10 см. Какова площадь его полной поверхности? а) 400 см2; б) 160 см2; в) 280 см2; г) 340 см2. 6) По стороне основания а и боковому ребру b найдите полную поверхность правильной треугольной призмы. а)  ; б) + 3ab; в) a2 + 3ab; г) 3a ( + 2).III. Решение задач: №№ 227, 228, 236, 237. Домашнее задание: теория (п. 30), №№ 238, 295, 297. Дополнительно (см.: Зив Б. Г., Мейлер В. М., Баханский А. Г. Задачи по геометрии. – М.: Просвещение, 1997.). 1 1) В наклонной треугольной призме ABCA1B1C1 основанием служит прямоугольный треугольник АВС (  С = 90°). Плоскость боковой грани АА1С1С перпендикулярна плоскости основания. Докажите, что СС1В1В – прямоугольник.2) В наклонной треугольной призме угол между двумя боковыми гранями прямой. Площади этих граней равны 50 и 120 см2. Длина бокового ребра 10 см. Найдите площадь боковой поверхности призмы. 2 1) Основанием наклонного параллелепипеда ABCDA1B1C1D1 служит прямоугольник ABCD. Плоскости граней AA1D1D и ВВ1С1С перпендикулярны плоскости основания. Докажите, что остальные боковые грани – прямоугольники. 2) В наклонной треугольной призме АВСА1В1С1 угол между гранями АА1С1С и СС1В1В прямой. Найдите площадь боковой поверхности призмы, если боковое ребро равно 5 см, а площади граней АА1В1В и СС1В1В равны соответственно 130 и 50 см2. 3 1) Основанием наклонной треугольной призмы ABCA1B1C1 служит равнобедренный треугольник АВС, АВ = АС, А1АС = А1АВ < 90°. Докажите, что СС1В1В – прямоугольник.2) В наклонной треугольной призме площади двух боковых граней равны 40 и 80 см2. Угол между ними равен 120°. Найдите площадь боковой поверхности призмы, если длина бокового ребра равна 10 см. 4 1) Основанием наклонной треугольной призмы ABCA1B1C1 служит правильный треугольник АВС. Вершина А1 равноудалена от всех вершин нижнего основания. Докажите, что СС1В1В – прямоугольник. 2) В наклонной треугольной призме площади двух боковых граней равны 6 и 3  см2. Угол между ними равен 135°. Найдите площадь боковой поверхности призмы, если длина бокового ребра равна 3 см.Урок 4 ПРИЗМА Цель: сформировать навык решения задач по изученной теме. Ход урока Решение задач: №№ 232, 233, 234, 235. Домашнее задание: №№ 290, 296, 298. Урок 5 ПИРАМИДА Цель: ввести понятие пирамиды, площади полной поверхности пирамиды. Ход урока I. Объяснение нового материала построить в соответствии с пунктом 28. Контрольные вопросы. 1. Среди изображенных тел выберите номера тех, которые являются пирамидами.  1 2 3 4 5  6 7 8 9 2. Назовите:
3. Продолжите предложения. 1) Высотой пирамиды называется… 2) Апофемой пирамиды называется… 3) Площадью полной поверхности пирамиды называется… 4) Площадью боковой поверхности пирамиды называется… 5) Диагональное сечение пирамиды – сечение пирамиды плоскостью, проходящей через два несоседних… II. Решение задач: №№ 240, 241, 242, 245. Домашнее задание: теория (п. 32), №№ 239, 243, 244. Урок 6 ПИРАМИДА. ПРАВИЛЬНАЯ ПИРАМИДА Цель: ввести понятие правильной пирамиды. |
