Поурочные разработки по геометрии 10 класс Атанасян (1). Урок 1 предмет стереометрии. Аксиомы стереометрии цель рассмотреть основные свойства плоскости
 Скачать 1.97 Mb.
|
|
ГЛАВА 4 ВЕКТОРЫ В ПРОСТРАНСТВЕ 6 ЧАСОВ. Урок 1 ПОНЯТИЕ ВЕКТОРА. РАВЕНСТВО ВЕКТОРОВ Цель: ввести понятие вектора в пространстве. Ход урока I. При объяснении нового материала можно организовать работу учащихся с учебником (п. 38–39) по плану: 1. Что такое вектор? 2. Какой вектор называется нулевым? 3. Что такое длина вектора? 4. Какие векторы называются коллинеарными? 5. Какие векторы называются равными? II. Решение задач: №№ 320 (а), 321 (а), 322, 323, 324, 325. Домашнее задание: теория (п. 38–39), №№ 320 (б), 321 (б), 326. Урок 2 ДЕЙСТВИЯ НАД ВЕКТОРАМИ Цель: ввести правила сложения и вычитания векторов, умножения вектора на число. Ход урока I. Устная работа.
II. Объяснение нового материала (п. 36 – 38). I. Сумма векторов.
Правило многоугольника  III. Решение задач: №№ 327, 328, 333 (а), 335 (а). II. Два ненулевых вектора называются противоположными, если их длины равны и они противоположно направлены. IV. Решение задач: № 329. Разностью векторов  и  называется такой вектор, сумма которого с вектором равна вектору , то есть  ,  . .
V. Решение задач: №№ 330, 331, 333 (б), 337 (б, в). III. Умножение вектора на число. Произведением ненулевого вектора на числ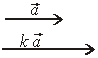о k называется такой вектор , длина которого равна  , причем векторы и сонаправлены при k ≥ 0 и противоположно направлены при k < 0. Произведением нулевого вектора на любое число считается нулевой вектор. 1. k > 0 2. k < 0   Векторы и k коллинеарны для любого и числа k, инаоборот, если векторы и коллинеарны и ≠  , то существует такое число k, что = k .VI. Решение задач: №№ 343, 344, 347 (а). Домашнее задание: теория (п. 40–42). №№ 334, 335 (б, в, г), 336, 347 (б). Урок 3 ДЕЙСТВИЯ НАД ВЕКТОРАМИ Цель: сформировать навык действий над векторами в пространстве. Ход урока I. Устная работа. №№ 327, 328, 329, 332 (предварительно рисунки и условие вынести на доску). II. Решение задач: №№ 339, 341, 345, 348, 349, 351, 352. № 352.  и  – коллинеарны   .Имеем  ,  или  .Следовательно, и коллинеарны.Домашнее задание: теория (п. 40–42), №№ 340, 346, 353. Урок 4 КОМПЛАНАРНЫЕ ВЕКТОРЫ Цели: ввести понятие компланарных векторов, правило сложения для трех некомпланарных векторов; доказать теорему о разложении любого вектора по трем некомпланарным векторам. Ход урока I. Объяснение нового материала построить в соответствии с пунктами 39 – 41 учебника. II. Решение задач. №№ 355, 356, 358 (а, б), 360 (а), 361. Домашнее задание: теория (п. 43–45), №№ 357, 358 (в, г, д), 360 (б), 362. Урок 5 КОМПЛАНАРНЫЕ ВЕКТОРЫ Цель: сформировать навык разложения вектора по трем некомпланарным векторам. Ход урока Решение задач: №№ 363, 364, 365, 367. Домашнее задание: №№ 366, 368, 369. Урок 6 ВЕКТОРЫ В ПРОСТРАНСТВЕ Цель: подготовить учащихся к контрольной работе. Ход урока Вариант I 1. Дан параллелепипед ABCDA1B1C1D1. Изобразите на рисунке векторы, равные: 1)  ;2)  .2. В тетраэдре DABC точка Е – середина DB, а М – точка пересечения медиан грани АВС. Разложите вектор  по векторам  ,  и  .3. Даны три неколлинеарных вектора , и  . Найдите значение k, при котором векторы  и  коллинеарны.4*. В кубе ABCDA1B1C1D1 точки Е и F – середины отрезков BD и С1С. Докажите, используя векторы, что прямые ВС1, EF и DC параллельны одной плоскости. Вариант II 1. Дан параллелепипед ABCDA1B1C1D1. Изобразите на рисунке векторы, равные: 1)  ;2)  .2. В тетраэдре DABC М – точка пересечения медиан грани ACD, а K – середина АВ. Разложите вектор  по векторам  ,  и  .3. Докажите, что векторы ,  и  компланарны.4*. В пространстве расположен параллелограмм ABCD и произвольный четырехугольник A1B1C1D1. Докажите, что точки пересечения медиан треугольников A1BB1, В1СС1, С1DD1 и А1АD1 являются вершинами параллелограмма. Домашнее задание: карточки. Вариант I 1. DABC – правильная треугольная пирамида. Сторона основания равна  . Боковые ребра наклонены к основанию под углом 60°. Найдите:  .2. Ребро куба ABCDA1B1C1D1 равно 1. Найдите:  .3. ABCDA1B1C1D1 – параллелепипед. АС1 пересекает B1D в точке М.  . Найдите х.4. ABCDA1B1C1D1 – параллелепипед. Укажите какой-нибудь вектор с началом и концом в вершинах параллелепипеда, который был бы компланарен с векторами  и  .5.  . Могут ли прямые АС и BD быть скрещивающимися?6.  ;  ;  ;  . Укажите тройку компланарных векторов.7. ABCDA1B1C1D1 – параллелепипед. Найдите:  .8. ABCDA1B1C1D1 – параллелепипед. D1C пересекает С1D в точке М. Выразите вектор  через векторы  и .9. PABCD – пирамида, ABCD – параллелограмм,  ;  ;  . Выразите вектор  через векторы , и .10. В правильной треугольной пирамиде DABC отрезок DO – высота. Разложите вектор  по векторам , и .Вариант II 1. Основанием пирамиды МАВС служит прямоугольный треугольник АСВ (  С = 90°); АС = 6; ВС = 8. Боковые ребра пирамиды наклонены к основанию под углом 60°. Найдите:  .2. В правильной треугольной призме АВСА1В1С1 сторона основания равна 1, точка Е – середина А1С1. Найдите:  .3. ABCDA1B1C1D1 – параллелепипед, А1С пересекает B1D в точке М.  . Найдите х.4. ABCDA1B1C1D1 – параллелепипед, Е и F – середины AD и CD соответственно. Будут ли компланарны векторы ,  и  ?5.  ;  ;  ;  . Укажите тройку компланарных векторов.6.  . При всех х и y и  не являются коллинеарными. Могут ли пересекаться прямые АС и BD?7. ABCDA1B1C1D1 – параллелепипед. Найдите:  .8. ABCDA1B1C1D1 – параллелепипед. АВ1 пересекает А1В в точке Е. Выразите вектор  через векторы  и .9. В пирамиде ЕАВСD основанием служит параллелограмм АВСD.  ;  ;  ; . Выразите вектор  через векторы  ,  и  .10. В тетраэдре DАВС отрезки DE и CF – медианы грани BDC. DE пересекает CF в точке O. Выразите вектор через векторы  , и .Урок 7 КОНТРОЛЬНАЯ РАБОТА № 5 |
.
