Поурочные разработки по геометрии 10 класс Атанасян (1). Урок 1 предмет стереометрии. Аксиомы стереометрии цель рассмотреть основные свойства плоскости

• Название: Урок 1 предмет стереометрии. Аксиомы стереометрии цель рассмотреть основные свойства плоскости
• Дата: 11.10.2022
• Размер: 1.97 Mb.
• Имя файла: Поурочные разработки по геометрии 10 класс Атанасян (1).doc
• Тип: Урок; #727176
• страница: 8 из 13

Ход урока

I. Актуализация знаний.

1. Дано: AD (АВС), АВ = 5, АС = 4, СВ = 3, AD = 6. Определите вид Δ АСВ. Найдите DC и DB. AD – перпендикуляр к плоскости, DC – наклонная, AC – проекция этой наклонной на плоскость (АВС).

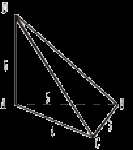
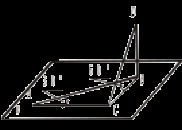
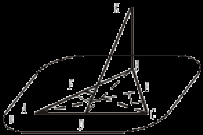
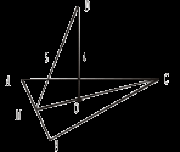
По условию задачи проекция АС перпендикулярна прямой СВ, проходящей через основание наклонной – точку С.

Вы доказали, что и наклонная DС перпендикулярна прямой СВ.

Сможем ли мы доказать это утверждение без метрических данных?

2. Дано: AD (АВС), АСВ = 90°. Доказать, что: а) AD CB; б) СВ (ADC); в) СВ CD. Какое утверждение вы доказали? Это утверждение получило название теоремы о трех перпендикулярах.

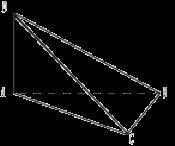
Учитель формулирует теорему о трех перпендикулярах. Доказывает её вместе с учащимися.

Сформулируйте обратную теорему, докажите ее (№ 153).

II. Решение задач: №№ 145, 146, 147.

III. Домашнее задание: теория (п. 20), №№ 148, 149, 150.

№ 150.

Дано: ABCD – прямоугольник, АK (АВС), KD = 6 см, KВ = 7 см, KС = 9 см. Найдите ρ(K, (АВС)), ρ (АK, CD).

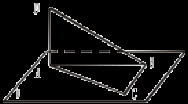
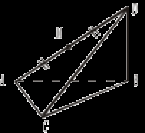
Решение

1. ρ (K, (АВС)) = АK.

2.

3. Δ KВС – прямоугольный. CB = см.

4. Δ AKD – прямоугольный. AK = = 2 см.

5. ρ(АK, CD) = АD; AD = 4 см.

Урок 9
ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ

Цель: сформировать навык применения теоремы о трех перпендикулярах к решению задач.

Ход урока

I. Проверка домашнего задания (теорема, №№ 149, 150).

II. Устная работа.

	1. Верно ли утверждение: «Если прямая, принадлежащая плоскости, перпендикулярна проекции наклонной на эту плоскость, то она перпендикулярна и самой наклонной»? (Верно.) Обоснуйте ответ.
		2. Верно ли утверждение: «Если прямая перпендикулярна проекции наклонной, то эта прямая перпендикулярна наклонной»? (Неверно.) Какое условие теоремы о трех перпендикулярах здесь не выполняется? (Прямая не принадлежит плоскости.)

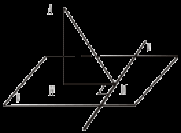
3. Установите по рисункам положение прямых а и b.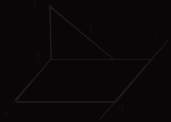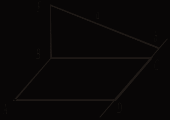



ABCD – прямоугольник, ABCD – прямоугольник,

BF 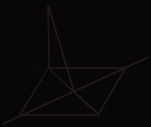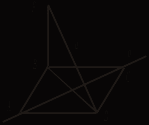(АВС) BF (АВС)



ABCD – ромб, ABCD – ромб,

BF (АВС) BF (АВС)

III. Решение задач (по готовым чертежам).

	1. В кубе ABCDA1B1C1D1: 1) ребро А1В1перпендикулярно диагонали В1С грани ВСС1В1; 2) диагональ А1С перпендикулярна диагонали BD основания ABCD. Докажите.
	2. 1) Дано: А = 30°; АВС = 60°, DB АВС. Докажите, что СD АС.
	2) Дано: ВАС = 40°, АСВ = 50°, AD АВС. Докажите, что СВ BD.
	3. 1) Дано: МА (АВС), АВ = АС, CD = BD. Докажите, что MD ВС 2) Дано: МА (АВС), BD = CD, MD ВС. Докажите, что АВ = АС.
	4. Дано: АЕ и CF – высоты, ВK АВС. Докажите, что KD АС.
	5. Дано: Δ АВС, BD (АВС), АМ = MD, М – центр описанной около Δ АDС окружности. Найдите ACD + ACB.

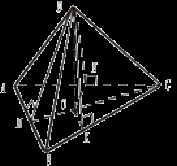
IV. Решение задач: №№ 154, 156.

Домашнее задание: №№ 155, 159.

Урок 10
ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ

Цель: сформировать навык применения теоремы о трех перпендикулярах к решению задач.

Ход урока

I. Проверка домашнего задания (теорема, №№ 155, 159).

II. Устная работа.

	1. АМ (АВС), АВ = АС, CD = DB. Докажите, что MD ВС.
		2. ABCD – параллелограмм, BM (АВС), МС DC. Определите вид параллелограмма ABCD.
		3. ABCD – параллелограмм, CM (АВС), МO BD. Определите вид параллелограмма ABCD.
		4. Δ АВС, С = 90°, О – центр описанной окружности, АМ = МС, OD (АВС), АВ = 5, АС = 3. Найдите DM.
		5. Δ АВС, АВ = ВС = АС, CD (АВС),АМ = МВ, DM = 15, CD = 12. Найдите SADB.
		6. Δ АВС, С = 90°, BD (АВС), AD = 2 BD. Найдите 1 + 2.
		7. ABCD – квадрат, ВЕ (АВС), ЕАВ = 45°, SABCD = 4. Найдите SΔAЕС.

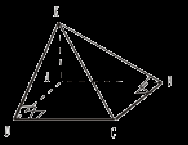
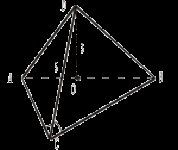
III. Решение задач.

1. Если точка равноудалена от всех сторон многоугольника, то она проецируется на его плоскость в центр вписанной окружности.

Дано: ML АВ, MN АС, МK ВС, МО (АВС). Доказать, что О – центр вписанной в Δ АВС окружности.

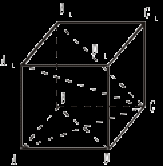
Доказательство

1)

2) Аналогично ОK ВС, ON АС.

3) OL = OK = ON (как проекции равных наклонных).

4) Точка О равноудалена от всех сторон треугольника, следовательно, является центром вписанной в него окружности.

2. Докажите обратное утверждение: «Если через центр вписанной в n-угольник окружности проведена прямая, перпендикулярная плоскости этого n-угольника, то каждая точка этой прямой равноудалена от сторон этого n-угольника». (Для доказательства можно использовать тот же рисунок). №№ 157, 158.

Домашнее задание: №№ 160, 205.

Урок 11
ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ

Цель: сформировать навык решения задач по изученной теме.

Ход урока

I. Проверка домашнего задания (№№ 160, 205).

II. Решение задач (по готовым чертежам).

	1. Δ АВС, D (АВC), AD = BD = СD, АОВ = 60°. Найдите АСВ.
	2. Δ АВС, АВ = ВС = АС, О – центр Δ АВС, DO (АВС), DC = 10, DO = 8. Найдите SАВС, расстояние от точки D до сторон Δ АВС.
	3. Δ АВС, АВ = ВС = АС, О – центр Δ АВС, DO (АВС), DМ = 5, DO = 4. Найдите РΔАВС, AD, BD, DC.
	4. Δ АВС, АСВ = 90°, АО = ОВ, DO (АВС), DC = 5, DO = 3. Найдите R описанной около Δ АВС окружности, АВ, AD, DB.
	5. Δ АВС, АС = СВ = 10, АВ = 12, DM АВ, DN АС, DK ВС, DM = DN = DK, DO (АВС), DO = 1. Найдите DC.