Поурочные разработки по геометрии 10 класс Атанасян (1). Урок 1 предмет стереометрии. Аксиомы стереометрии цель рассмотреть основные свойства плоскости
 Скачать 1.97 Mb. Скачать 1.97 Mb.
|
|
III. Решение задач: №№ 199, 202, 203, 207. Домашнее задание: №№ 204, 206. Урок 12 УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ Цели: ввести понятие прямоугольной проекции фигуры; дать определение угла между прямой и плоскостью. Ход урока I. Объяснение нового материала построить в соответствии с п. 21. II. Решение задач: №№ 151, 163, 208, 209. III. Решение задач (по готовым чертежам).
Домашнее задание: теория (п. 21), №№ 164, 165. Урок 13 ЛАБОРАТОРНО-ПРАКТИЧЕСКАЯ РАБОТА Цели: сформировать конструктивный навык нахождения угла между прямой и плоскостью; расстояния от точки до прямой; научить обосновывать или опровергать выдвигаемые предположения. Ход урока Учащимся выдаются готовые бланки, на которых они выполняют задания. Лабораторно-практическая работа построена на основе варьирования условий. «Одинаковые» картинки и разные к ним условия должны заставить учащихся думать, обосновывать или опровергать свои гипотезы, научить применять изученные теоретические положения. Учитель должен требовать от учащихся проговаривания всех определений и теорем. I. Расстояние от точки до прямой 1. AF Найти расстояние от F до CВ.
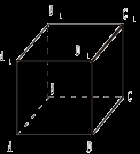
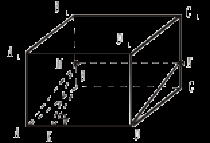
2. Найти расстояние от F до АС.   FB ABCD – прямоугольник ABCD – ромб II. Угол между прямой и плоскостью 1. Найдите угол между B1D и (АВС); между B1D и (DD1C1).   ABCD – прямоугольник ABCD – параллелограмм АА1 2. ВВ1 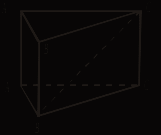  Δ АВС – равносторонний Δ АВС – прямоугольный (  Δ АВС – тупоугольный (
4. BD Найти угол между CD и плоскостью (АВD).
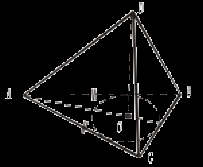
Урок 14 ДВУГРАННЫЙ УГОЛ Цель: ввести определение двугранного угла. Ход урока I. Объяснение нового материала. Пункт 22 можно прочитать вместе с учащимися. Один из механизмов построения линейного угла двугранного угла приведен в задаче № 166. Покажите использование данного механизма. ABCD – квадрат, FO
Δ DFC – равнобедренный  3.  – линейный угол угла ADCF. – линейный угол угла ADCF.II. Провести аналогичные рассуждения и выполнить построения.
III. Решение задач: №№ 170, 171. Домашнее задание: теория (п. 22), №№ 167, 168, 169, 172. Урок 15 ДВУГРАННЫЙ УГОЛ Цели: сформировать конструктивный навык нахождения угла между плоскостями; отработать определение двугранного угла. Ход урока 1. FO ABCD – квадрат ABCD – ромб 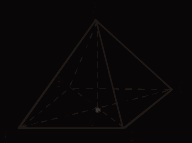  Найдите угол между (АВС) и (FDC); Найдите угол между (FDC) и (FBC). 2. FB ABCD – прямоугольник ABCD – ромб 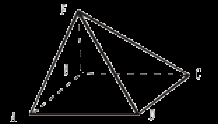  Найдите угол между (АВС) и (FDC); Найдите угол между (AFB) и (FBC); Найдите угол между (AFD) и (FBC). 3. AF
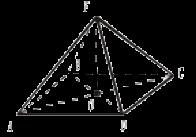
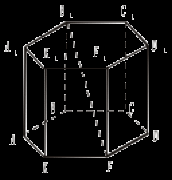
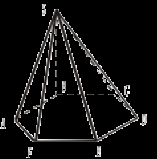
Найти угол между (АВС) и (FCВ). 4. ABCDEF – правильный шестиугольник SB
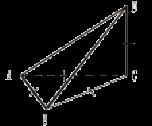
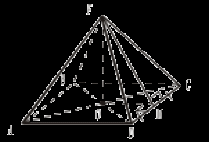
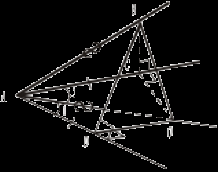
Урок 16 ДВУГРАННЫЙ УГОЛ Цель: сформировать навык решения задач по данной теме. Ход урока Решение задач: №№ 173, 176, 212, 213 (решите эту задачу, используя результат задачи № 212: SАВС = Sпр ∙ cos α), 214 (решите двумя способами). Домашнее задание: №№ 174, 175, 216. Урок 17 СВОЙСТВО ДВУГРАННОГО УГЛА Цель: доказать одно из свойств двугранного угла, часто применяющееся при решении задач. Ход урока Если два плоских угла трехгранного угла равны, то их общее ребро проецируется на биссектрису третьего плоского угла.
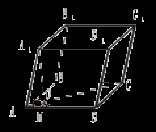
2. Δ ADO = Δ АСО (как прямоугольные по гипотенузе и катету) I. Решение задач. № 1. Все грани параллелепипеда – равные ромбы, со стороной а и острым углом α. Найдите высоту параллелепипеда. Решение
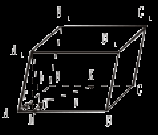
3. Проведем ОМ По теореме о трех перпендикулярах А1М 4. Δ АА1М – прямоугольный. AM = a ∙ cos α. 5. Δ АОМ – прямоугольный. АО =  . .6. Δ А1АО – прямоугольный. H = А1О =  . .№ 2. Основанием параллелепипеда является прямоугольник со сторонами а и b. Боковое ребро длины с образует со смежными сторонами основания углы, равные φ. Найдите высоту параллелепипеда. Решение
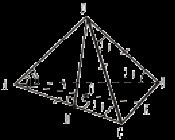
3. Проведем ОМ 4. Δ А1АМ – прямоугольный. AM = c ∙ cos φ. 5. Δ АОМ – прямоугольный. АО = 6. Δ А1АО – прямоугольный. H = А1О = № 3. Все грани тетраэдра АBCD – равные равнобедренные треугольники с боковыми сторонами, равными а, и углом между ними – 2α. Найдите высоту тетраэдра. Решение
3. Δ MDC – прямоугольный. DM = a ∙ sin 2α. MC = a ∙ cos 2α. 4. AM = AC – MC = a – a ∙ cos 2α = a (1 – cos 2α) = 2a sin2α. 5. Δ AOM – прямоугольный. OM = AM ∙ tg α = 2a sin2α ∙ tg α. 6. H = DO = = Домашняя контрольная работа Вариант I 1. Чему равен угол между ребром двугранного угла и любой прямой, лежащей в плоскости его линейного угла? 2. Треугольник АВС – прямоугольный ( 3. Через вершину прямого угла С равнобедренного прямоугольного треугольника АВС проведена плоскость α, параллельная гипотенузе и составляющая с катетом угол 30°. Найдите угол между плоскостью АВС и плоскостью α. Вариант II 1. Плоскость α пересекает грани двугранного угла по прямым АВ и АС. Две пересекающиеся прямые, лежащие в плоскости α, перпендикулярны к ребру этого угла. Докажите, что 2. ABCD – ромб. 3. Через сторону ромба ABCD проведена плоскость α. Сторона АВ составляет с этой плоскостью угол 30°. Найдите угол между плоскостью ромба и плоскостью α, если острый угол ромба равен 45°. Урок 18 ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ Цель: ввести определение перпендикулярных плоскостей, доказать признак перпендикулярности плоскостей. Ход урока I. Объяснение нового материала построить в соответствии с пунктом 23. Перед доказательством теоремы рассмотрите модели многогранников.
Когда можно утверждать, что плоскости перпендикулярны? Выскажите предположение. Сформулировать признак. Доказать. II. Решение задач: №№ 177, 179, 181, 183, 184. Домашнее задание: теория (п. 23), №№ 178, 180, 182, 185. Урок 19 ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД Цели: ввести понятие прямоугольного параллелепипеда; доказать свойство диагоналей прямоугольного параллелепипеда. Ход урока I. Проверка домашнего задания (признак). II. Устная работа.
4. Плоскость линейного угла двугранного угла перпендикулярна каждой его грани. Доказать. III. Объяснение нового материала. Выставить на стол как можно больше параллелепипедов (прямых, наклонных, прямоугольных, кубов) разных размеров и цветов. Попросить одного ученика убрать со стола все наклонные параллелепипеды, оставить только прямые. Далее из оставшихся прямых параллелепипедов убрать те, в основании которых не лежит прямоугольник. Все оставшиеся – это прямоугольные параллелепипеды (в том числе и кубы). Какой параллелепипед называется прямоугольным? (Прямой, в основании которого лежит прямоугольник.) Сформулировать определение, доказать свойства прямоугольного параллелепипеда, используя для их открытия аналогию с прямоугольником.
Рассмотреть куб как прямоугольный параллелепипед, у которого все три основания равны. IV. Решение задач: №№ 187 (а), 188, 193, 195. Домашнее задание: теория (п. 24), №№ 187 (б, в), 189, 191, 192, 217. Урок 20 ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД Цель: сформировать навык решения задач по изученной теме. Ход урока См. Крамор В. С. «Повторяем и систематизируем школьный курс геометрии». – М.: Просвещение, 1993. А 1. Измерения прямоугольного параллелепипеда равны 6, 4 и 12 м. Найдите диагональ параллелепипеда. (Ответ: 14 м.) 2. Измерения комнаты равны 6, 8 и 3 м. Найдите площадь всех ее стен, пола и потолка. (Ответ: 180 м2.) 3. Площадь полной поверхности прямоугольного параллелепипеда равна 352 м2. Найдите его измерения, если они относятся как 1 : 2 : 3. (Ответ: 4 м, 8 м и 12 м.) 4. В прямоугольном параллелепипеде стороны основания относятся как 7 : 24, а площадь диагонального сечения равна 50 м2. Найдите площадь боковой поверхности. (Ответ: 124 м2.) В 1. Площадь диагонального сечения куба равна k. Найдите ребро куба, диагональ основания, диагональ куба, площадь его полной поверхности. (Ответ:  .) .)2. Диагональ прямоугольного параллелепипеда равна k и составляет с плоскостью основания угол α, а с большей боковой гранью угол β. Найдите площадь боковой поверхности параллелепипеда. (Ответ: С 1. Диагональ прямоугольного параллелепипеда образует с меньшей боковой гранью угол β. Через большие стороны верхнего и нижнего оснований проведено сечение, образующее с плоскостью основания угол α. Зная, что периметр этого сечения равен Р, найдите измерения параллелепипеда. (Ответ: большая сторона  , меньшая сторона , меньшая сторона  , H = , H = .) .)2. Диагональная плоскость прямоугольного параллелепипеда и лежащая в ней диагональ k образуют с одной и той же боковой гранью соответственно углы α и β. Найдите измерения параллелепипеда. (Ответ: k sin β, k sin β ctg α,  α, β – острые углы.) α, β – острые углы.)Урок 21 ПОДГОТОВКА К КОНТРОЛЬНОЙ РАБОТЕ Ход урока Вариант I 1. В треугольнике АВС АС = СВ = 10 см, 2. Точка М равноудалена от всех вершин равнобедренного прямоугольного треугольника АСВ ( 1) Докажите, что плоскость АМВ перпендикулярна плоскости АВС. 2) Какой угол плоскость ВМС составляет с плоскостью АВС? 3) Найдите угол между МС и плоскостью АВС. 3*. Найдите расстояние от точки Е – середины стороны АВ – до плоскости ВМС. Вариант II 1. Через сторону АС треугольника АВС проведена плоскость α, удаленная от вершины В на расстояние, равное 4 см, АС = ВС = 8 см, = 22°30′. Найдите угол между плоскостями АВС и α. 2. ABCD – квадрат со стороной, равной 4 см. Треугольник АМВ имеет общую сторону АВ с квадратом, АМ = ВМ = 2 1) Докажите, что ВС 2) Найдите угол между МС и плоскостью квадрата. 3*. Найдите расстояние от точки А до плоскости DMC. Вариант III 1. ABCD – ромб со стороной 4 см, 2. Точка М равноудалена от всех сторон правильного треугольника АВС, сторона которого равна 4 см. Расстояние от точки М до плоскости АВС равно 2 см. 1) Докажите, что плоскость АМО перпендикулярна плоскости ВМС (О – основание перпендикуляра, опущенного из точки М на плоскость АВС). 2) Найдите угол между плоскостью ВМС и плоскостью АВС. 3) Найдите угол между МС и плоскостью АВС. 3*. Точка Е принадлежит АС, причем АЕ : ЕС = 2 : 1. Найдите расстояние от точки Е до плоскости ВМС. Вариант IV 1. Через сторону AD ромба ABCD проведена плоскость α, удаленная от ВС на расстояние, равное 3 2. Треугольник АСВ – прямоугольный ( 1) Докажите, что МС 2) Найдите угол между МВ и плоскостью АВС. 3*. Найдите расстояние от середины АВ – точки Е – до плоскости ВМС. Домашнее задание: карточки. Вариант I 1. АВ 2. К плоскости проведены равные наклонные. Равны ли их проекции? 3. Точка М равноудалена от всех вершин прямоугольного треугольника, катеты которого 6 см и 8 см. Расстояние от точки М до плоскости треугольника равно 12 см. Найдите расстояние от точки М до вершин треугольника. 4. Основанием прямоугольного параллелепипеда является квадрат со стороной, равной а. Расстояние от бокового ребра до скрещивающейся с ним диагонали параллелепипеда равно…
7. Основанием прямоугольного параллелепипеда служит квадрат со стороной, равной 4. Диагональ параллелепипеда равна 8. Угол между диагональю и боковой гранью равен… 8. Точка М равноудалена от всех сторон квадрата ABCD, сторона которого равна 8 см. Расстояние от точки М до плоскости квадрата равно 4 см. Угол между плоскостью (MCD) и плоскостью квадрата равен… 9. Прямая а и плоскость α перпендикулярны плоскости β. Каково взаимное расположение прямой а и плоскости α? 10. Треугольник МАВ и квадрат ABCD имеют общую сторону АВ, и их плоскости взаимно перпендикулярны. Угол MAD равен… Вариант II 1. АВ 2. Две наклонные, проведенные к плоскости, имеют равные проекции. Равны ли сами наклонные? 3. Точка D равноудалена от всех вершин правильного треугольника и находится на расстоянии 3 см от его плоскости. Высота треугольника равна 6 см. Расстояние от точки D до вершин треугольника равно… 4. Основанием прямоугольного параллелепипеда служит квадрат со стороной, равной а. Расстояние между скрещивающимися диагоналями противоположных граней параллелепипеда равно…
7. В прямоугольном параллелепипеде основанием служит квадрат. Диагональ параллелепипеда равна 10 см и составляет с плоскостью боковой грани угол 60°. Найдите стороны основания. 8. Точка D равноудалена от всех сторон правильного треугольника АВС. Расстояние от точки D до плоскости треугольника равно 2 9. Две плоскости перпендикулярны к третьей. Линии пересечения этих плоскостей с третьей плоскостью параллельны. Каково взаимное положение этих плоскостей? 10. Прямоугольный треугольник АСВ ( УРОК 22 КОНТРОЛЬНАЯ РАБОТА №3 Контрольная работа № 3 Вариант I 1. Диагональ куба равна 6 см. Найдите: а) ребро куба; б) косинус угла между диагональю куба и плоскостью одной из его граней. 2. Сторона АВ ромба ABCD равна a, один из углов равен 60°. Через сторону АВ проведена плоскость α на расстоянии а) Найдите расстояние от точки С до плоскости α. б) Покажите на рисунке линейный угол двугранного угла DABM, М в) Найдите синус угла между плоскостью ромба и плоскостью α. Вариант II 1. Основанием прямоугольного параллелепипеда служит квадрат; диагональ параллелепипеда равна 2 а) измерения параллелепипеда; б) синус угла между диагональю параллелепипеда и плоскостью его основания. 2. Сторона квадрата ABCD равна а. Через сторону AD проведена плоскость α на расстоянии а) Найдите расстояние от точки С до плоскости α. б) Покажите на рисунке линейный угол двугранного угла BADM, М в) Найдите синус угла между плоскостью квадрата и плоскостью α. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


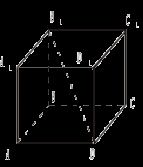
 биссектрисе
биссектрисе 
 биссектрисе
биссектрисе 
 биссектрисе
биссектрисе  AK – медиана и высота. О
AK – медиана и высота. О