Поурочные разработки по геометрии 10 класс Атанасян (1). Урок 1 предмет стереометрии. Аксиомы стереометрии цель рассмотреть основные свойства плоскости
 Скачать 1.97 Mb. Скачать 1.97 Mb.
|
|
II. Решение задач. Варианты I и IV рассмотреть в классе. Варианты II и III дать домой для самостоятельного решения. Вариант I
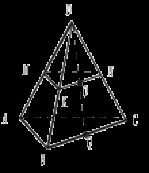
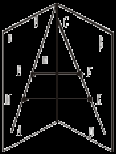
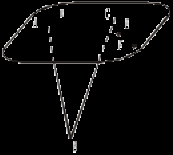
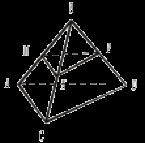
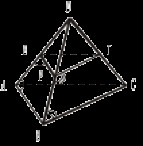
2. Треугольники АВС и ADC лежат в разных плоскостях и имеют общую сторону АС. Точка Е лежит на стороне АВ, F – на стороне ВС, причем EF параллельна плоскости ADC. Р – середина AD, а K – середина DC. 1) Докажите, что EF || PK. 2) Каково взаимное положение прямых РK и АВ? Чему равен угол между этими прямыми, если 3. Плоскости α и β пересекаются по прямой m. Прямая а лежит в плоскости α. Каково возможное взаимное положение прямой а и плоскости β? Сделайте рисунок и поясните. 4*. Используя рисунок, постройте линию пересечения плоскости EFM с плоскостью α. Поясните. 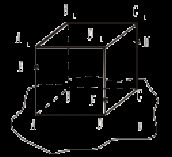 Вариант IV 1. На рисунке точки Е и F лежат в плоскости β, а М – в плоскости α. Постройте линии пересечения плоскости EFM с плоскостями α и β. Поясните. 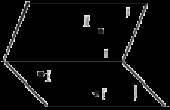 2. Основание AD трапеции ABCD лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно. 1) Докажите, что BCFE – параллелограмм. 2) Каково взаимное положение прямых EF и АВ? Чему равен угол между ними, если 3. Отрезок АВ параллелен плоскости α, а отрезок CD лежит в этой плоскости, причем AB = CD. Можно ли утверждать, что четырехугольник ABDC – параллелограмм? Поясните.
Вариант II
2. Треугольники ABC и DCE лежат в разных плоскостях и имеют общую вершину С, АВ || DE. 1) Постройте линию пересечения плоскостей АВС и DCE. Поясните. 2) Каково взаимное положение прямых АВ и DF, где F лежит на стороне CE? Чему равен угол между этими прямыми, если 3. Прямая а параллельна плоскости α, точка М и прямая с лежат в плоскости α (М
Вариант III
2. Трапеция ABCD (AD и ВС – основания) и треугольник AED имеют общую сторону AD и лежат в разных плоскостях. Точка М лежит на стороне АЕ, а Р – на стороне DE, причем МР параллельна плоскости трапеции. 1) Докажите, что МР || ВС. 2) Каково взаимное положение прямых МР и АВ? Чему равен угол между этими прямыми, если 3. Плоскости α и β пересекаются по прямой m. Прямая а лежит в плоскости α, а b – в плоскости β. Какие возможны взаимные положения прямых а и b? Сделайте рисунок и поясните.
Урок 12 КОНТРОЛЬНАЯ РАБОТА № 1 Ход урока Вариант I 1. В каком случае три точки в пространстве не определяют положение плоскости, проходящей через эти точки? 2. Могут ли две различные плоскости иметь только одну общую точку? 3. Точка М не лежит на прямой а. Через точку М проводятся прямые, пересекающие прямую а. Лежат ли эти прямые в одной плоскости? 4. Каково взаимное положение прямых: 1) AD1 и MN; 2) AD1 и ВС1; 3) MN и DC? (Рис. 1.) 5. Прямые а и b скрещиваются с прямой с. Могут ли прямые а и b пересекаться?  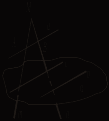 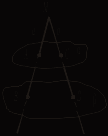 Рис. 1 Рис. 2 Рис. 3 6. Прямая а параллельна плоскости α. Существуют ли на плоскости α прямые, не параллельные а? Если да, то каково их взаимное положение? 7. На рисунке 2 прямые m и n пересекаются в точке М, А 8. Даны треугольник АВС и плоскость α, АВ || α; АС || α. Каково взаимное положение прямой ВС и плоскости α? 9. На рисунке 3 плоскости α и β параллельны. Пересекающиеся в точке М прямые а и b пересекают плоскость α в точках А и С, а плоскость β – в точках В и D, 10. Плоскость α пересекает только боковые ребра параллелепипеда. Определите вид сечения. Вариант II 1. Что можно сказать о взаимном положении двух плоскостей, имеющих три общие точки, не лежащие на одной прямой? 2. Могут ли две различные плоскости иметь только две общие точки? 3. Прямые а и b пересекаются в точке М. Прямая с, не проходящая через точку М, пересекает прямые а и b. Лежат ли все эти три прямые в одной плоскости? 4. Каково взаимное положение прямых: 1) A1D и MN; 2) A1D и В1С; 3) MN и А1В1? (Рис. 1.) 5. Прямые а и b скрещиваются с прямой с. Могут ли прямые а и b быть параллельными?  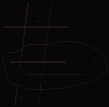 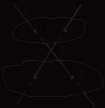 Рис. 1 Рис. 2 Рис. 3 6. Две прямые параллельны одной и той же плоскости. Можно ли утверждать, что эти прямые параллельны между собой? Если нет, то каково их взаимное положение? 7. На рисунке 2 прямые m и n параллельны. Точки А и В соответственно принадлежат прямым m и n; b лежит в плоскости α, а || b. Каково взаимное положение прямых b и с? 8. Даны четырехугольник АВСD и плоскость α. Его диагонали АС и BD параллельны плоскости α. Каково взаимное положение АВ и плоскости α? 9. На рисунке 3 плоскости α и β параллельны. Пересекающиеся в точке М прямые а и b пересекают плоскость α соответственно в точках В и А, а плоскость β – в точках Е и F. 10. Плоскость α проходит через диагональ основания параллелепипеда и середину одной из сторон верхнего основания. Определите вид сечения. Урок 13 ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ. ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ДВУХ ПЛОСКОСТЕЙ Цели: ввести понятие параллельных плоскостей; доказать признак параллельности двух плоскостей. Ход урока I. Объяснение нового материала построить в соответствии с пунктом 11 учебника.
Доказательство 1.  2. 2.  3. Пусть αβ, тогда α 4.  5. 5.  6. а || с, b || c, но а Полученное противоречие доказывает, что наше предположение неверно. Следовательно, α || β. II. Решение задач. № 48 (устно). № 49.
3.  № 50.
2.  Получили противоречие условию, которое опровергает наше предположение. Следовательно, m || β. № 54.
Решение 1. MN – средняя линия Δ АВС 2. NP – средняя линия Δ CBD 3.  по признаку. по признаку.4. Δ MNP Δ ADC, K = Домашнее задание: теория (п. 10), №№ 51, 52, 53. Урок 14 СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЕЙ Цели: доказать теорему существования и единственности плоскости, параллельной данной и проходящей через данную точку пространства; рассмотреть свойства параллельных плоскостей. Ход урока I. Проверка домашнего задания (у доски). II. Устная работа. 1. Верно ли, что если две пересекающиеся прямые, лежащие в одной плоскости, параллельны другой плоскости, то эти плоскости параллельны. (Верно.) 2. Верно ли, что если две прямые, лежащие в одной плоскости, параллельны двум прямым другой плоскости, то эти плоскости параллельны. (Нет. Привести контрпример – пересекающиеся плоскости, проведенные через параллельные прямые.)
4. Каким может быть взаимное расположение прямой а и плоскости β, если прямая а лежит в плоскости α, параллельной плоскости β? 5. Как могут быть расположены плоскости α и β, если плоскость α проходит через некоторую прямую а, параллельную плоскости β? 6. Как могут быть расположены плоскости α и β, если любая прямая, лежащая в плоскости α, параллельна плоскости β? III. Объяснение нового материала построить как процесс решения задач в соответствии с пунктом 11 учебника. IV. Решение задач: №№ 55, 56, 58, 59, 60. № 55. Дано: а Доказать, что а
2.  (задача № 55). (задача № 55).Получили противоречие условию. Следовательно, наше предположение неверно и а № 60.
Проведем (а, С) = Q1, Q1 Причем а || а1 и b || b1, а1 3. Аналогично проведем рассуждения для плоскостей β и χ. Получим в плоскости β прямые а2 и b2. Причем а1 || а2, b1 || b2. 4. 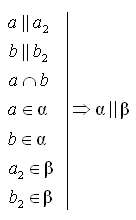 по признаку. по признаку.Домашнее задание: теория (п. 11), №№ 57, 61, 104. Урок 15 ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ. СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЕЙ Цель: сформировать навык применения изученных свойств параллельных плоскостей при решении задач. Ход урока I. Проверка домашнего задания (у доски). II. Устная работа.
III. Решение задач. №№ 63, 64, 65 (устно), 107. Домашняя контрольная работа Вариант I 1. Параллелограммы ABCD и ADFE лежат в разных плоскостях и имеют общую сторону AD. Прямая m, параллельная BC, пересекает плоскости АВЕ и DCF соответственно в точках Н и Р. Докажите, что HPFE – параллелограмм. 2. На рисунке 1 плоскости α и β параллельны, а || а1. Прямая а пересекает плоскости α и β соответственно в точках А и В, а прямая а1 пересекает плоскость α в точке А1. Постройте точку пересечения а1 с плоскостью β. Поясните. 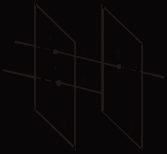 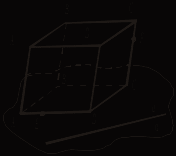 Рис. 1 Рис. 2 3. В тетраэдре DABC 4*. Постройте сечение параллелепипеда плоскостью, проходящей через точки Е и F и параллельной прямой а (рис. 2). Вариант II 1. Вне плоскости αрасположен треугольник АВС, у которого медианы АА1 и ВВ1 параллельны плоскости α. Через вершины В и С треугольника проведены параллельные прямые, которые пересекают плоскость α соответственно в точках Е и F. Докажите, что ECBF – параллелограмм. 2. На рисунке 1 плоскости α и β параллельны. Прямая а пересекает плоскости α и β соответственно в точках А и В, а прямая b – в точках С и D. Найдите взаимное положение прямых а и b. Поясните. 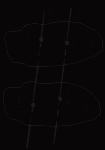 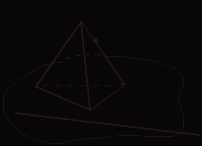 Рис. 1 Рис. 2 3. Все грани параллелепипеда ABCDA1B1C1D1 – квадраты со стороной а. Через середину AD параллельно плоскости DA1B1 проведена плоскость. Найдите периметр сечения. 4*. Постройте сечение тетраэдра плоскостью, проходящей через точки С и К и параллельной прямой а (рис. 2). Вариант III 1. Прямоугольники ABCD и EBCF лежат в разных плоскостях и имеют общую сторону ВС. Прямая а параллельна AD и пересекает плоскости АВЕ и DCF соответственно в точках Р и Н. Докажите, что РВСН – параллелограмм. 2. На рисунке 1 плоскости α и β параллельны. Прямые а и b пересекаются в точке М. Прямая а пересекает плоскости α и β соответственно в точках А и В, а прямая b пересекает плоскость β в точке D. Постройте точку пересечения прямой b с плоскостью α. 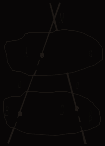 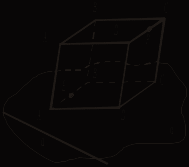 Рис. 1 Рис. 2 3. В тетраэдре DABC точка М – середина АС, DB = 6, MD = 10, DBM = 90°. Постройте сечение тетраэдра плоскостью, проходящей через середину ребра DC и параллельной плоскости DMB, и найдите площадь сечения. 4*. Постройте сечение параллелепипеда плоскостью, проходящей через точки Е и Р и параллельной прямой а (рис. 2). Вариант IV 1. Трапеция ABCD (AD и ВС – основания) расположена вне плоскости α. Диагонали трапеции параллельны плоскости α. Через вершины А и В проведены параллельные прямые, которые пересекают плоскость α в точках Е и F соответственно. Докажите, что EABF – параллелограмм. 2. На рисунке 1 плоскости α и β параллельны. Прямая а пересекает плоскости α и β соответственно в точках А и В, а прямая b – в точках С и D. Каково взаимное положение прямых а и b? Поясните. 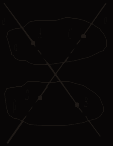 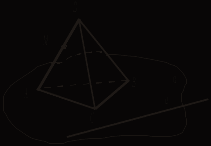 Рис. 1 Рис. 2 3. Дан параллелепипед ABCDA1B1C1D1, все грани которого – прямоугольники, AD = 4, DC = 8, СС1 = 6. Постройте сечение параллелепипеда плоскостью, проходящей через середину ребра DC и параллельной плоскости AB1C1, и найдите периметр сечения. 4*. Постройте сечение тетраэдра плоскостью, проходящей через точки С и М и параллельной прямой а (рис. 2). Урок 16 ТЕТРАЭДР Цель: ввести понятие тетраэдра, проиллюстрировать изученные понятия, связанные со взаимным расположением прямых и плоскостей на примере треугольной пирамиды. Ход урока I. Объяснение нового материала построить в соответствии с пунктом 12. II. Решение задач: №№ 66, 67, 68 (на готовом чертеже), 69, 70, 74. № 69.
Доказательство 1. 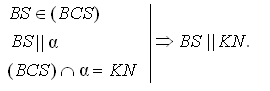 2.  3.  № 70.
Доказательство 1. MK || ВС (по свойству средней линии). 2. MN || BD (по свойству средней линии). 3.  . .№ 74.
Решение 1.  2. Аналогично MK || AB, MN || AC. 3. Δ BCD Δ KND (по двум углам) DN = 4.  5. Δ MDK Δ ADB (по двум углам) 6. Аналогично, MN = 7. Δ MNK Δ ABC (по трем сторонам). 8.  . .Домашнее задание: теория (п. 12), №№ 71, 102, 103. Урок 17 ПАРАЛЛЕЛЕПИПЕД Цель: ввести понятие параллелепипеда, рассмотреть свойства ребер, граней, диагоналей параллелепипеда. Ход урока I. Объяснение нового материала построить в соответствии с пунктом 13 учебника. II. Решение задач: №№ 76 (устно), 77, 78 (устно по готовому чертежу), 79, 80. III. Домашнее задание: теория (п. 13), №№ 81, 109, 110. Подготовить ответы на вопросы к главе I. Урок 18 ЗАДАЧИ НА ПОСТРОЕНИЕ СЕЧЕНИЙ Цель: сформировать навык решения простейших задач на построение сечений тетраэдра и параллелепипеда. Ход урока I. Устная работа – вопросы к главе I. II. Решение задач: №№ 72, 73, 75, 82. III. Домашнее задание: теория (п. 14), №№ 83, 84, 85, 86. Дополнительно: 1. ABCD – тетраэдр, М – середина АС, DB = 6, MD = 10,
SDBM = 24 см2 2. Все грани параллелепипеда – прямоугольники.
Урок 19 КОНТРОЛЬНАЯ РАБОТА № 2 Домашняя контрольная работа 1. Через точку K, не лежащую между параллельными плоскостями α и β, проведены прямые а и b. Прямая а пересекает плоскости α и β в точках А1 и А2соответственно, b – в точках В1 и В2.
|

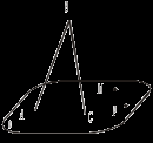




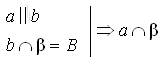 по лемме.
по лемме.