Поурочные разработки по геометрии 10 класс Атанасян (1). Урок 1 предмет стереометрии. Аксиомы стереометрии цель рассмотреть основные свойства плоскости
 Скачать 1.97 Mb. Скачать 1.97 Mb.
|
|
III. Решение задач: №№ 90 (устно), 91, 92, 93, 96. Домашняя контрольная работа Вариант I 1. Через сторону АС треугольника АВС проведена плоскость α. В 2. Дан Δ MKP. Плоскость, параллельная прямой МK, пересекает МР в точке М1, РK – в точке K1. Найдите М1K1, если МР : М1Р = 12 : 5, МK = 18 см. 3. Точка Р не лежит в плоскости трапеции ABCD (AD || BC). Докажите, что прямая, проходящая через середины РВ и РС, параллельна средней линии трапеции. Вариант II 1. Через основание AD трапеции ABCD проведена плоскостьα. ВС 2. Дан Δ BCE. Плоскость, параллельная прямой СЕ, пересекает ВЕ в точке Е1, а ВС – в точке С1. Найдите ВС1, если С1Е1: СЕ = 3 : 8, ВС = = 28 см. 3. Точка Е не лежит в плоскости параллелограмма АВСD. Докажите, что прямая, проходящая через середины АЕ и ВЕ, параллельна прямой СD. Урок 7 СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ Цель: доказать признак скрещивающихся прямых, теорему о проведении через одну из скрещивающихся прямых плоскости, параллельной другой прямой. Ход урока I. Работа над ошибками. II. Объяснение нового материала. Вспомнить различные случаи взаимного расположения прямых в пространстве (урок № 6). Рассмотреть различные пары скрещивающихся прямых на моделях многоугольников, наблюдая факт, зафиксированный в признаке скрещивающихся прямых.
Если учащиеся упустили выделенный в формулировке факт, то привести контрпример – пересекающиеся прямые. Доказать признак скрещивающихся прямых. Для «открытия» учащимися факта второй теоремы опять обратиться к рассмотрению моделей, каждый раз отвечая на вопросы: назовите плоскость, проходящую через одну из скрещивающихся прямых параллельно другой прямой? Сколько таких плоскостей? При рассмотрении третьей модели должна возникнуть проблема – можно ли через одну из скрещивающихся прямых построить плоскость, параллельную другой прямой? Учащимся предлагается построить такую плоскость.
Построение 1. Построить MN 2. (MN, AB) ≡ α. 3. α – единственная. Таким образом, мы доказали теорему, что через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна. III. Решение задач. № 34 (решать устно, требовать, чтобы учащиеся проговаривали формулировки признаков). № 36.
Через какие прямые мы можем провести плоскость? (Через пересекающиеся, через параллельные.) Если мы проведем плоскость α через пересекающиеся прямые а и с, то прямая b, будет параллельна плоскости α. То есть нужно провести плоскость αчерез параллельные прямые а и b. 1. (a, b) ≡ α. 2.  3.  (по признаку). (по признаку).Домашнее задание: теория (п. 7), № 35 (воспользуйтесь методом от противного), № 37. Урок 8 СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ Цель: закрепить навык использования признака скрещивающихся прямых при решении задач. Ход урока I. Опрос у доски (знание теорем, их доказательств). II. Проверка домашнего задания. III. Устная работа. 1. Какие прямые называются скрещивающимися? 2. Сформулируйте признак скрещивающихся прямых. 3. Выясните взаимное расположение прямых:
4. Верно ли утверждение: если две прямые не имеют общих точек, то они параллельны? 5. Две прямые параллельны некоторой плоскости. Могут ли эти прямые: а) пересекаться? б) быть скрещивающимися? 6. Могут ли скрещивающиеся прямые а и b быть параллельными прямой с? Ответ обоснуйте. 7. Даны две скрещивающиеся прямые а и b. Точки А и А1 лежат на прямой а, точки В и В1 – на прямой b. Как будут расположены прямые АВ и А1В1? 8. Прямая а скрещивается с прямой b, а прямая b скрещивается с прямой с. Следует ли из этого, что прямые а и с скрещиваются? 9. Каково должно быть взаимное расположение трех прямых, чтобы можно было провести плоскость, содержащую все прямые? 10. Можно ли провести прямую, пересекающую каждую из трех скрещивающихся прямых? 11. Даны две пересекающиеся плоскости α иβ. В плоскости α лежит прямая а, а в плоскости β – прямая b. Лежат ли прямые а и b в одной плоскости, если известно, что они пересекают линию пересечения плоскостей α иβ: а) в одной точке; б) в разных точках? 12. Даны две параллельные плоскости α иβ.В плоскости α лежит прямая а, а в плоскости β – прямая b. Каковы возможные случаи взаимного расположения прямых а и b? 13. В плоскости двух параллельных (пересекающихся) прямых а и b дана точка С, не лежащая на этих прямых. Прямая с проходит через точку С. Как может быть расположена прямая с относительно прямых а и b? IV. Решение задач. № 39.
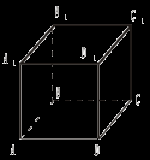
2.  3.  (по признаку). (по признаку).№ 41. Дано: а b. Может ли а || с и b || c. Пусть а || с и b || c, тогда а || b. Противоречие условию. № 42.
1.  2. Так как в трапецию можно вписать окружность, то АВ + ЕK = = АK + ВЕ. РABEK = 2 ∙ (22,5 + 27,5) = 2 ∙ 50 = 100 см. № 43.
2. NP – средняя линия Δ АDB 3. 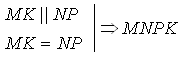 – параллелограмм. – параллелограмм.№ 101.
2. MNPK – параллелограмм (аналогично) = Q1Р. 3. 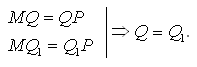 4. MP Домашнее задание: теория (п. 7), №№ 38, 93, 94, 100. Урок 9 УГЛЫ С СОНАПРАВЛЕННЫМИ СТОРОНАМИ. УГОЛ МЕЖДУ ПРЯМЫМИ Цель: доказать теорему об углах с сонаправленными сторонами. Ход урока I. Повторение пройденного. Продолжите предложение. 1. Если две прямые в пространстве не имеют общих точек, то они… 2. Если две прямые не принадлежат одной плоскости, то они… 3. Если ABCD – пирамида, то прямые АВ и СD… 4. ABCDA1B1C1D1 – куб. Прямые АВ и СС1… 5. Геометрическое место прямых, пересекающих одну из скрещивающихся прямых и параллельных другой, есть… II. Объяснение нового материала. Пункты учебника (п. 8, 9) можно прочитать вместе с учащимися. Проверить осознанность усвоения теоремы об углах с соноправленными сторонами, можно, попросив учащихся доказать теорему на видоизмененном чертеже, составить план доказательства.  III. Решение задач №№ 44, 45, 47. Домашнее задание: теория (п. 8 – 9); №№ 46, 97. Уроки 10–11 АКСИОМЫ СТЕРЕОМЕТРИИ. ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ Цель: повторить теорию, подготовить учащихся к контрольной работе. Ход уроков I. Устная работа. 1. Прямая пересекает две стороны треугольника. Лежит ли она в плоскости этого треугольника? 2. Прямая пересекает вершину треугольника. Лежит ли она в плоскости этого треугольника? 3. Три вершины параллелограмма лежат в плоскости. Принадлежит ли четвертая вершина параллелограмма этой плоскости? 4. Хорда окружности принадлежит плоскости. Верно ли утверждение, что и вся окружность лежит в этой плоскости? 5. Две пересекающиеся хорды окружности принадлежат плоскости. Верно ли утверждение, что любая точка окружности принадлежит этой плоскости? 6. Сколько плоскостей можно провести через: три различные точки; две различные точки; через прямую и не лежащую на ней точку; через две параллельные прямые? 7. Верно ли утверждение: любые три точки принадлежат плоскости; через любые три точки проходит единственная плоскость? 8. Известно, что прямая параллельна плоскости. Параллельна ли она любой прямой, лежащей в этой плоскости? Может ли данная прямая пересечь какую-либо прямую, лежащую в плоскости? 9. Средняя линия трапеции лежит в плоскости α. Пересекают ли основания трапеции эту плоскость? 10. Прямая а параллельна линии пересечения плоскостей α и β. Каково взаимное расположение а и α; а и β? 11. Прямая b непараллельна линии пересечения плоскостей α и β. Каково взаимное расположение b и α; b и β? 12. Сколько можно провести через данную точку: прямых, параллельных данной плоскости; плоскостей, параллельных данной прямой? 13. Стороны АВ и ВС параллелограмма ABCD пересекают некоторую плоскость. Докажите, что прямые AD и DC пересекают эту плоскость. 14. Плоскость αпараллельна одной из двух параллельных прямых. Каково взаимное расположение второй прямой и плоскости α? 15. Сторона АВ параллелограмма ABCD лежит в плоскости α.Докажите, что сторона CD параллельна этой плоскости. 16. Прямая пересекает плоскость. Можно ли в плоскости провести прямую, параллельную данной прямой? 17. Две прямые параллельны одной плоскости. Можно ли утверждать, что эти прямые параллельны? 18. Каким может быть взаимное расположение двух прямых, из которых одна параллельна некоторой плоскости, а другая пересекает эту плоскость? 19. Прямые а и b скрещиваются с прямой с. Могут ли прямые а и b быть параллельными? Пересекаться? 20. Может ли каждая из двух скрещивающихся прямых быть параллельна третьей прямой? 21. Прямая, не лежащая в плоскости параллелограмма, параллельна одной из его диагоналей. Каково взаимное расположение данной прямой и второй диагонали? 22. Как могут быть расположены прямая и плоскость, если данная прямая и некоторая прямая, лежащая в этой плоскости, скрещиваются? |