Поурочные разработки по геометрии 10 класс Атанасян (1). Урок 1 предмет стереометрии. Аксиомы стереометрии цель рассмотреть основные свойства плоскости
 Скачать 1.97 Mb. Скачать 1.97 Mb.
|
|
Ход урока I. Объяснение нового материала начать с рассмотрения взаимного расположения прямой и плоскости в пространстве.  В каком случае прямая и плоскость называются параллельными? Прямая и плоскость называются параллельными, если они не имеют общих точек. Покажите на предметах обстановки классной комнаты прямые, параллельные плоскости пола, плоскости стены.
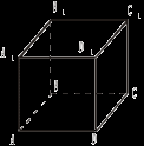
Обратите внимание на модель куба. DC || (АА1В1). В плоскости (АА1В1) имеется прямая AB, параллельная DC. DC || (А1В1С1). В плоскости (А1В1С1) имеется прямая D1C1, параллельная DC. Сделайте предположение. Сформулируйте и докажите признак параллельности прямой и плоскости. II. Решение задач.
Доказательство 
Доказательство 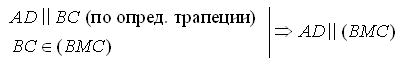 по признаку. по признаку.
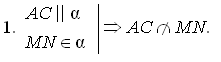 2.  по определению. по определению.3. Δ АВС Δ MBN по двум углам.
Решение 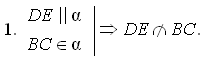 2.  по определению. по определению.3. Δ АВС Δ ADE по двум углам. BC = Домашнее задание: теория (п. 6), №№ 23, 25, 27. Урок 5 ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ Цель: продолжить формирование навыка применять изученные теоремы к решению задач. Ход урока I. Проверка домашнего задания (у доски). II. Устная работа. 1. Каково может быть взаимное расположение прямой и плоскости в пространстве? 2. В каком случае прямая и плоскость называются параллельными? Пересекающимися? 3. Сформулируйте признак параллельности прямой и плоскости. 4. Верно ли утверждение, что если прямая, не лежащая в плоскости, параллельна ей, то она параллельна любой прямой, лежащей в этой плоскости? 5. Верно ли утверждение, что если две прямые параллельны одной и той же плоскости, то они параллельны между собой? 6. Можно ли построить плоскость, проходящую через данную прямую и параллельную другой данной прямой? 7. Сколько можно провести через данную точку: а) прямых, параллельных данной плоскости; б) плоскостей, параллельных данной прямой? 8. Каким может быть взаимное расположение двух прямых, из которых одна параллельна некоторой плоскости, а другая пересекает эту плоскость? III. Решение задач. Задача 1. Доказать, что если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
2.  по определению а || b. по определению а || b.Задача 2. Доказать, что если через каждую из двух параллельных прямых проведена плоскость, причем эти плоскости пересекаются, то линия их пересечения параллельна каждой из данных прямых.
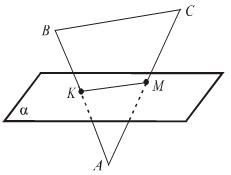
2.  по предыдущему утверждению а || с. по предыдущему утверждению а || с.3. Аналогично, b || c. Задача 3. Доказать, что если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.
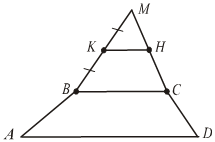
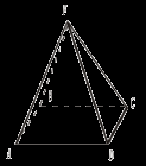
Тогда  по лемме a по лемме a Полученное противоречие опровергает предположение. Задача 4. Постройте сечение тетраэдра ABCD плоскостью, проходящей через вершину С, внутреннюю точку М ребра АВ и параллельной прямой AD. Построение
3.  4. (MNC) – искомое сечение. Найдите площадь полученного сечения, если каждое ребро тетраэдра имеет длину а и точка М является серединой ребра АВ. № 29.
2.  3. AD || BC, AD || KH 4. BK = KH, KH || BC Следовательно, KН – средняя линия Δ BMC. KH = 6 см. Домашнее задание. № 30.
Доказательство 1. Пусть CD  по лемме AB по лемме AB Полученное противоречие опровергает предположение. Следовательно, CD 2. 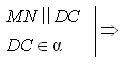 по признаку MN || α. по признаку MN || α.№ 31.
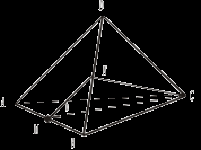
2. 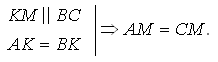 № 32 (разобрать доказательство самостоятельно). Урок 6 ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ, ПРЯМОЙ И ПЛОСКОСТИ Цели: систематизировать материал изученного параграфа; проверить уровень сформированности умения применять полученные знания к решению задач. Ход урока I. Проверка домашнего задания (у доски). II. Устная работа. 1. Верна ли формулировка признака параллельности прямой и плоскости: «Прямая, параллельная какой-либо прямой на плоскости, параллельна и самой плоскости». (Нет, прямая может лежать в плоскости). 2. Прямые а и b параллельны. Какое положение может занимать прямая а относительно плоскости, проходящей через прямую b? 3. Даны прямая и две пересекающихся плоскости. Охарактеризовать все возможные случаи их взаимного расположения. 4. Одна из двух параллельных прямых параллельна некоторой плоскости. Можно ли утверждать, что и вторая прямая параллельна этой плоскости? Ответ обоснуйте. 5. Даны две пересекающиеся плоскости. Существует ли плоскость, пересекающая две данные плоскости по параллельным прямым? 6. Даны две скрещивающиеся прямые. Можно ли через одну из этих прямых провести плоскость, параллельную другой? 7. В плоскости α даны две пересекающиеся прямые а и b. Точка С не лежит в плоскости α. Каковы возможные случаи расположения прямой, проходящей через точку С, относительно прямых а и b? 8. Дано: FABCD – пирамида, ABCD – параллелограмм.
|


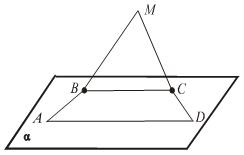
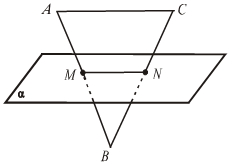
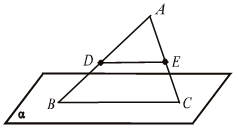
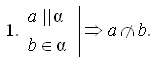
 по признаку а || β.
по признаку а || β.