Поурочные разработки по геометрии 10 класс Атанасян (1). Урок 1 предмет стереометрии. Аксиомы стереометрии цель рассмотреть основные свойства плоскости
 Скачать 1.97 Mb. Скачать 1.97 Mb.
|
|
Домашнее задание: теория (п. 17), №№ 129, 131. Урок 4 ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ Цель: сформировать навык применения признака перпендикулярности прямой и плоскости к решению задач. Ход урока I. Проверка домашнего задания (теорема, №№ 129, 131). II. Устная работа. 1. Можно ли утверждать, что прямая, проходящая через центр круга перпендикулярна: а) диаметру; б) двум радиусам; в) двум диаметрам, перпендикулярна плоскости круга? (а) нет; б) нет; в) да.) 2. Можно ли утверждать, что прямая перпендикулярна плоскости, если она перпендикулярна лежащим в этой плоскости: а) двум сторонам треугольника; б) двум сторонам квадрата; в) диагоналям параллелограмма. 3. Дано ABCD – куб. Заполните пропуски о взаимном расположении прямых и плоскостей:
4. Три луча ОМ, ON, ОК попарно перпендикулярны. Как расположен каждый из лучей по отношению к плоскости, определяемой двумя другими лучами? Что моделирует в классной комнате описанную комбинацию? III. Решение задач.
2. Δ ADС = Δ ВDС (по двум сторонам и углу между ними) 3.  4.  5.  Урок 5 ТЕОРЕМА О ПЛОСКОСТИ, ПЕРПЕНДИКУЛЯРНОЙ ПРЯМОЙ. ТЕОРЕМА О ПРЯМОЙ, называется перпендикулярной плоскости, если она перпендикулярна некоторой прямой, лежащей в этой плоскости?»">ПЕРПЕНДИКУЛЯРНОЙ ПЛОСКОСТИ Цель: доказать теоремы существования и единственности прямой (плоскости), перпендикулярной к данной плоскости (прямой). Ход урока I. Объяснение нового материала. Доказать теорему существования и единственности плоскости, проходящей через любую точку пространства перпендикулярно к данной прямой (п. 17, № 133). Составить обратную теорему, доказать (п. 18). II. Решение задач. №№ 123, 132, 135, 137. III. Домашнее задание: теория (п. 17 – 18), № 134. Урок 6 ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ Цель: проверить знание учащимися основных теоретических положений изученной темы. Ход урока I. Диктант. Закончите предложения. Сделайте рисунок. 1. Две прямые называются перпендикулярными, если… 2. Прямая называется перпендикулярной к плоскости, если… 3. Прямая перпендикулярна плоскости, если она… 4. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то… 5. Через данную точку пространства можно провести прямую, ей перпендикулярную, и притом… 6. Все прямые, проходящие через данную точку прямой и перпендикулярные к этой прямой, лежат в… 7. Если одна из двух параллельных прямых перпендикулярна плоскости, то… 8. Две прямые, перпендикулярные одной и той же плоскости,… 9. Если плоскость перпендикулярна одной из двух параллельных прямых, то… 10. Если две плоскости перпендикулярны прямой, то они… II. Решение задач.
2. 
Домашнее задание: 1. Через катеты BD и BC прямоугольных треугольников ABD и ABC проведена плоскость α, не содержащая их общий катет. Будет ли АВ 2. Отрезок MH пересекает некоторую плоскость в точке K. Через концы отрезка проведены прямые НР и МЕ, перпендикулярные плоскости и пересекающие ее в точках Р и Е. Найдите РЕ, если НР = 4 см, НK = 5 см, МЕ = 12 см. 3. ABCD – квадрат. Отрезок MD перпендикулярен к плоскости АВС. Докажите, что MB 4. ABCD – прямоугольник. Отрезок АЕ перпендикулярен к плоскости АВС. ЕВ = 15, ЕС = 24, ED = 20. Докажите, что треугольник EDC прямоугольный, и найдите АЕ. 5. Точка А принадлежит окружности, АK – перпендикуляр к ее плоскости, АK = 1 см, АВ – диаметр, ВС – хорда окружности, составляющая с АВ угол 45°. Радиус окружности равен 2 см. Докажите, что треугольник KСВ прямоугольный, и найдите KС. Урок 7 РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ Цели: ввести понятие расстояния от точки до плоскости; перпендикуляра к плоскости из точки; наклонной, проведенной из точки к плоскости; основания наклонной; проекции наклонной; рассмотреть связь между наклонной, её проекцией и перпендикуляром. Ход урока I. Устная работа. 1. Верно ли утверждение: «Прямая перпендикулярна плоскости, если она перпендикулярна двум прямым, лежащим в этой плоскости»? 2. Верно ли утверждение: «Прямая называется перпендикулярной плоскости, если она перпендикулярна некоторой прямой, лежащей в этой плоскости»? 3. Как расположены по отношению друг к другу ребра, выходящие из одной вершины куба? 4. Как расположены плоскости верхней и нижней граней по отношению к боковым ребрам? 5. Что можно сказать о двух (трех, четырех) прямых, перпендикулярных к одной плоскости? 6. Верно ли утверждение: «Две прямые, перпендикулярные третьей прямой, параллельны»? II. Объяснение нового материала.
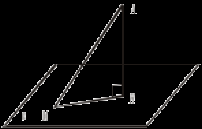 III. Решение задач: №№ 138 (а), 139, 140, 143. № 143.
2.Δ АОМ = Δ ВОМ = Δ СОМ (как прямоугольные по гипотенузе и катету) 3. R =  см. см.4. Δ МОС – прямоугольный, МО = Если точка равноудалена от всех вершин многоугольника, то во что она проецируется на его плоскости? Составьте обратное утверждение для № 143. Докажите, что любая точка прямой, перпендикулярной плоскости треугольника и проходящей через центр описанной около него окружности, равноудалена от всех его вершин. (Для доказательства можно использовать тот же рисунок.) Верно ли утверждение: «Любая точка прямой, проходящей через центр описанной около многоугольника окружности перпендикулярно к плоскости этого многоугольника, равноудалена от всех его вершин» (№ 200). Далее определяется расстояние между двумя параллельными плоскостями, между плоскостью и параллельной ей прямой (№ 144), между скрещивающимися прямыми (п. 19). Делаются соответствующие рисунки. Домашнее задание: теория (п. 19), №№ 138 (б), 141, 142. Урок 8 ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ Цель: доказать теорему о трех перпендикулярах. |