Разработки уроков. Урок 1
 Скачать 1 Mb.
|
|
IV. Итог урока. Домашнее задание: решить № 170 (г), 171, 172, 174, 178 (а). НОК. Урок 1 Цели: ввести понятие наименьшего общего кратного; изучить правило нахождения наименьшего общего кратного и научить учащихся находить его при решении задач. Ход урока I. Анализ самостоятельной работы. 1. Указать ошибки, допущенные учащимися при выполнении работы. 2. Решить на доске и в тетрадях задания, вызвавшие затруднения у учащихся. II. Устная работа. 1. Решить № 186 (а; б). 2. Решить № 189 (а; б) и № 190 (г). III. Объяснение нового материала. 1. Задача. Из порта А в порт В одновременно вышли два теплохода. Первый из них тратит на рейс туда и обратно 3 суток, а второй 4 суток. Через сколько суток оба теплохода окажутся снова вместе в порту А? Решение. Искомое число суток должно делиться и на 3, и на 4, то есть оно должно быть общим кратным чисел 3 и 4. Запишем кратные каждого из этих чисел в порядке возрастания: Числа, кратные 3: 3; 6; 9; 12; 15; 18; 21; 24; 27; 30; 33; 36. Числа, кратные 4: 4; 8; 12; 16; 20; 24; 28; 32; 36, … Общие кратные чисел 3 и 4 (они подчеркнуты): 12; 24; 36; … Наименьшее из этих чисел – число 12. Значит, через 12 суток оба теплохода окажутся снова вместе в порту А. При этом первый теплоход совершит за это время 4 рейса туда и обратно (12 : 3 = 4), а второй – 3 рейса (12 : 4 = 3). Наименьшее натуральное число, которое делится на каждое из данных натуральных чисел, называется наименьшим общим кратным. 2. Изучить по учебнику пункт 7 на с. 29–30. 3. Изучить правило нахождения наименьшего общего кратного для трех и более чисел. 4. Решить устно № 179 (а). IV. Закрепление изученного материала. 1. Решить № 180 (а; б) с комментированием. 2. Решить № 181 (а; г; е) на доске и в тетрадях. Решение. 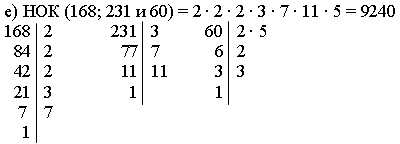 Ответ: 9240. 3. Повторение изученного ранее материала: а) Решить № 195 и № 196 с комментированием. б) Решить № 201, используя таблицу простых чисел на форзаце учебника. V. Итог урока. Вопросы: 1) Какое число называют наименьшим общим кратным натуральных чисел а и в? 2) Как найти наименьшее общее кратное нескольких чисел? 3) Какое число является наименьшим общим кратным чисел m и n, если число m кратно числу n? Домашнее задание: изучить п. 7; решить № 202 (а), № 203 (а), № 206 (а; в). Урок 2 Цели: способствовать выработке навыков нахождения наименьшего общего кратного; учить применять наименьшее общее кратное чисел при решении задач; развивать логическое мышление учащихся. Ход урока I. Устная работа. 1. Решить № 186 (в; г) и № 189 (в; г). 2. Укажите среди данных произведений разложение числа 700 на простые множители: а) 4 · 5 · 5 · 7; б) 2 · 2 · 7 · 25; в) 2 · 2 · 5 · 5 · 7; г) 2 · 14 · 25. Ответ: в). 3. Найдите НОД чисел 350; 420 и 210. Ответ: 70. 4. Найдите НОК чисел 40; 60 и 70. Ответ: 840. II. Выполнение упражнений. 1. Решить № 179 (б) и № 180 (в) на доске и в тетрадях. 2. Решить № 181 (в) (коллективное обсуждение решения, а затем самостоятельное решение учащимися). 3. Решить задачу № 184. Решение. 45 = 3 · 3 · 5; 60 = 2 · 5 · 2 · 3 НОК (45; 60) = 2 · 5 · 2 · 3 · 3 = 180. Ответ: 180 м. 4. Решить задачу. Какой наименьшей длины ленту должна купить Мальвина, чтобы разрезать ее на ленты по 35 см или по 50 см, не получив обрезков? Решение. 35 = 5 · 7; 50 = 2 · 5 · 5; НОК (35; 50) = 2 · 5 · 5 · 7 = 350. Ответ: 350 см = 3 м 50 см. 5. Проверить равенство НОК (а; в) · НОД (а; в) = а · в, если а = 28, в = 21. Решение. 28 = 2 · 2 · 7; 21 = 3 · 7. НОД (28; 21) = 7; НОК (28; 21) = 2 · 2 · 7 · 3 = 84. а · в = 28 · 21 = 588; НОК (а; в) · НОД (а; в) = 84 · 7 = 588. Равенство верно. III. Повторение ранее изученного материала. 1. Решить № 191. 2. Как находится среднее арифметическое чисел? Решить № 198. 3. Решить задачу № 199. Решение. Пусть второе число равно х, тогда первое число 2х. (х + 2х) : 2 = 54 3х = 54 · 2 3х = 108 х = 108 : 3 х = 36. Второе число равно 36, первое число 72. Ответ: 72 и 36. 4. Самостоятельно решить задание – найти наибольший общий делитель чисел: а) 465 и 870; б) 645 и 680. IV. Итог урока. 1. Повторить правило нахождения НОК. 2. Найти наименьшее общее кратное чисел (устно): а) 3 и 7; б) 8 и 6; в) 9 и 14; г) 180 и 120. Домашнее задание: изучить п. 7; решить № 202 (б; в), № 204, № 207, № 210 (а). Урок 3 Цель: тренировать учащихся в нахождении НОД и НОК чисел при выполнении упражнений. Ход урока I. Устная работа. 1. Решить № 188, 189 (д; е) и № 192. 2. Найти наибольший общий делитель и наименьшее общее кратное чисел: а) 5 и 25; б) 25 и 75; в) 8; 12 и 24; г) 18; 27 и 54; д) 60; 40; 120; е) 2 и 3; ж) 8 и 9; з) 5; 8 и 3; и) 120; 180 и 360. II. Тренировочные упражнения. 1. Решить № 180 (г) с комментированием. 2. Решить № 181 (д) на доске и в тетрадях. 3. Решить № 182 с обсуждением и решением в тетрадях. Записать вывод: наименьшее общее кратное двух взаимно простых чисел равно произведению этих чисел. 4*. Решить задачу: Саша ходит в бассейн один раз в 3 дня, Вася – в 4 дня, а Ваня – в 5 дней. Они встретились в бассейне в этот понедельник. Через сколько дней и в какой день недели они встретятся снова? Решение. НОК (3; 4; 5) = 60. Через 60 дней, в пятницу (60 : 7 = 8 недель и 4 дня пройдет) они встретятся снова. Ответ: через 60 дней, в пятницу. 5. Решить самостоятельно задачу: Какой наименьшей длины должна быть доска, чтобы ее можно было разрезать поперек на части, равные 20 см или 27 см, не получив обрезков? НОК (20; 27) = 540. Длина доски должна быть 540 см = 5 м 40 см. Ответ: 5 м 40 см. 6. Решить № 175 на доске и в тетрадях. Сделать вывод. III. Самостоятельная работа (10–15 мин). Вариант I. 1. Найдите наименьшее общее кратное чисел: а) 18 и 27; б) 7875 и 4725. 2. На базар привезли арбузы. Если их считать десятками, то получится целое число десятков. Если их считать дюжинами (по 12), то опять получится целое число дюжин. Сколько арбузов привезли на базар, если их больше 300, но меньше 400? 3. Проверьте равенство НОК (m; n) =  если m = 35, n = 49.Вариант II. 1. Найдите наименьшее общее кратное чисел: а) 40 и 56; б) 7425 и 4455. 2. Солдаты выстроились в ряды, по 12 человек в каждом, а затем перестроились по 8 человек в ряду. Сколько было солдат, если их больше 180, но меньше 200? 3. Проверьте равенство НОД (с; d) =  если с = 42, d = 35.IV. Итог урока. Повторить выводы упражнений № 182 и 183, придумать свои примеры. Домашнее задание: решить № 202 (г), № 205, № 208, № 210 (б). Урок 4 Цели: повторение и закрепление изученного материала, подготовка к контрольной работе; способствовать развитию навыков решения задач и упражнений. Ход урока I. Анализ самостоятельной работы. Указать сделанные учениками ошибки и решить задачи, вызвавшие затруднения у учащихся. II. Устные упражнения. 1. Решить № 190 (б; в) и № 193. 2. Решить № 187. III. Выполнение упражнений. 1. Решить № 181 (б) самостоятельно. 2. Найти наименьшее общее кратное чисел: а) 48 и 72; б) 350 и 420. 3. Найти наибольший общий делитель чисел 840 и 1260. 4. Доказать, что числа 136 и 119 не взаимно простые. 5. Решить задачу № 185. НОК (15; 20; 12) = 2 · 2 · 3 · 5 = 60 15 = 3 · 5; 20 = 2 · 5 · 2; 12 = 2 · 2 · 3. Ответ: через 60 суток. 6. Повторение материала: а) Решить задачу № 200 (1) с коллективным обсуждением и решением на доске и в тетрадях. б) Самостоятельно решить № 200 (2). Решение. 1) Пусть во второй день израсходовали х т керосина, тогда в первый день – 2,4х т. х + 2,4х = 38 –9,1 3,4х = 28,9 х = 28,9 : 3,4 = 289 : 34 х = 8,5. Во второй день израсходовали 8,5 т, тогда в первый день 20,4 т. Ответ: 20,4 т. 2) Пусть после обеда выдали у т муки, тогда до обеда выдали 3,2у т. у + 3,2у = 19 – 4,3 4,2у = 14,7 у = 14,7 : 4,2 = 147 : 42 у = 3,5. До обеда выдали 3,5 · 3,2 = 11,2 (т). Ответ: 11,2 т. IV. Итог урока. Беседа о свойствах НОД и НОК. Домашнее задание: решить № 203 (б), 206 (б; г), № 209, № 170 (б; в). СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ ДЕЛИТЕЛИ И КРАТНЫЕ Урок 1 Цели: ввести понятие делителей и кратных чисел; научить находить делители числа и кратные числа; развивать логическое мышление учащихся. Ход урока I. Анализ контрольной работы. Обратить внимание учащихся на сделанные ошибки, решив неправильно выполненные задания. II. Устная работа. 1. Решить № 222 (а; б). 2. Решить № 226, используя рисунок 12. III. Объяснение нового материала. 1. Объяснение учителем материала пункта 8 с использованием рисунка 8 учебника и модели «Доли. Дроби» (с. 34–35). 2. Записать в тетрадях основное свойство дроби: «Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь». Примеры: а) умножьте числитель и знаменатель каждой дроби на 2:  б) разделите числитель и знаменатель каждой дроби на 3:  IV. Закрепление изученного материала. 1. Решить устно № 211 по рисунку 9 учебника. 2. Решить устно № 212 (а; б) по рисунку 10. 3. Решить № 214 на доске и в тетрадях. Учитель пользуется цветными мелками, а ученики цветными карандашами при изображении отрезков. 4. Самостоятельно учащиеся выполняют задания № 216 и № 217 (с последующей проверкой). 5. Устно решить № 221 (а), № 213 (а; б) и № 219. V. Повторение ранее изученного материала. 1. Решить № 224 на доске и в тетрадях. Решение. а) 23 + 2,6 = 8 + 2,6 = 10,6; в) (1,6 –0,7)2 = 0,92 = 0,81; б) 0,32 + 1,1 = 0,09 + 1,1 = 1,19; г) (0,6 · 0,5 + 0,7)3 = (0,3 + 0,7)3 = 13 =1. 2. Решить № 231 на доске и в тетрадях (вызвать к доске сразу четвертых учащихся, они решают на доске, учащиеся самостоятельно решают в тетрадях, а затем проверяют решение). Решение.  НОД (2450; 3500) = 2 · 5 · 5 · 7 = 350. НОК (2450; 3500) = 2 · 5 · 2 · 5 · 5 · 7 · 7 = 3500 · 7 = 24500.  VI. Итог урока. Ответить на вопросы: 1) Сформулируйте основное свойство дроби. 2) Изменится ли дробь, если ее числитель и знаменатель умножить на 15, а потом разделить на 3? Домашнее задание: изучить п. 8; решить № 237, № 239 (а); № 241 (а). Урок 2 Цели: способствовать выработке навыков и умений учащихся при решении задач и упражнений; научить применять основное свойство дроби при выполнении упражнений. Ход урока I. Актуализация опорных знаний учащихся. 1. Двое учащихся работают на доске: а) первый решает задачу № 233 (1); б) второй учащийся решает № 241 (б). 2. Устно решить № 222 (в; г; д). 3. Устно решить № 223. II. Работа по учебнику. Прочитать по учебнику раздел «Говорите правильно» на странице 35. III. Выполнение упражнений. 1. По рисунку 10 устно решить № 212 (в; г). 2. Устно решить № 213 (а). Повторить основное свойство дроби. Решить № 220 на доске и в тетрадях. 3. Решить № 215, начертив на доске и в тетрадях координатный луч. 4. Решить устно № 218 и 221 (в –г) с коллективным обсуждением. 5. Повторение изученного материала: а) Решить № 230 (1) с комментированием. б) Устно решить № 234. в) Решить самостоятельно: № 235. 8,12 · 0,25 + 3,24 · 0,25 = 0,25 · (8,12 + 3,24) = 0,25 · 11,36 = 2,84. г) Решить № 233 (2). Решение. 1) 5,2 · 4,5 = 23,4 (км) прошли по дороге. 2) 32,4 – 23,4 = 9 (км) осталось пройти. 3) 9 : 2,5 = 90 : 25 = 3,6 (ч) шли по болотистой местности. 4) 4,5 + 1,6 + 3,6 = 9,7 (ч) затрачено на весь переход. Ответ: 9,7 ч. IV. итог урока. 1. Используя основное свойство дроби, найдите значения х: а)  2. Беседа об истории дробей (прочитать исторический материал на с. 116). Домашнее задание: выучить определения из п. 8; решить № 238, № 239 (б), № 240 (а; б; в), № 241 (б). СОКРАЩЕНИЕ ДРОБЕЙ Урок 1 Цели: повторить основное свойство дроби и научить применять его при сокращении дробей; дать определение несократимой дроби. Ход урока I. Устная работа. 1. Решить № 253 (а; б). 2. Решить № 256. Повторить основное свойство дроби. 3. Решить № 257 (а; б). II. Изучение нового материала. 1. Подготовительные упражнения к изучению нового материала: а) повторить основное свойство дроби; привести свои примеры; б) устно решить № 261 (а; б) и № 260 (а; б). 2. Числитель и знаменатель дроби  При этом получилась дробь, значение которой равно данной дроби, но с меньшими числителем и знаменателем. Такое преобразование называют сокращением дроби.3. Определение сокращения дроби. 4. При сокращении дроби изменится лишь ее запись, числовое значение дроби не меняется. 5. Дробь  сократить нельзя, так как числа 3 и 4 – взаимно простые числа. Такую дробь называют несократимой.Записать в тетрадях определение: Дробь, числитель и знаменатель которой числа взаимно простые, называетсянесократимой. 6. Дробь  можно сразу сократить на наибольший общий делитель числителя и знаменателя, то есть на 60: но можно вести постепенно:  Дробь сокращают до тех пор, пока не получат в числителе и знаменателе взаимно простые числа. 7. Иногда удобно при сокращении дроби разложить числитель и знаменатель на несколько множителей, а потом уже сократить. Например,  Сократим на 3 · 3 · 5 и получим  Дробь несократимая. |