Разработки уроков. Урок 1

• Название: Урок 1
• Анкор: Разработки уроков
• Дата: 09.06.2022
• Размер: 1 Mb.
• Имя файла: razrabotki_urokov_6_klass.docx
• Тип: Урок; #580245
• страница: 2 из 27

Цели: изучить признак делимости на 3; закрепить знание признаков делимости на 9, на 2, на 5 и на 10; развивать логическое мышление учащихся.

Ход урока

I. Устная работа.

1. Решить № 69 (3-е и 4-е задания каждого столбика).

2. Решить № 72 (а; б).

3. Решить № 76, № 77 и № 78 (повторить признаки делимости на 10 и на 5).

II. Объяснение нового материала.

1. Разделим на 3 каждое из чисел:

162, 201, 111, 205, 317, 824. Обнаружим, что первые три числа делятся на 3, а последние три числа не делятся на 3. Обратим внимание, что сумма цифр каждого из трех первых чисел делится на 3.

2. Сформулировать признак делимости на 3.

3. Выпишите числа, которые делятся на 3:

123; 110; 834; 2383; 882; 1111.

4. Верно ли утверждение:

а) Если число делится на 9, то оно делится на 3? Ответ объясните.

б) Если число делится на 3, то оно делится на 9? Привести примеры.

5. Придумайте 3 числа, которые:

а) делятся на 2 и на 3;

б) делятся на 3 и на 5;

в) делятся на 10 и на 9.

III. Закрепление изученного материала.

1. Самостоятельно решить № 65 и № 63.

2. Решить № 71 (а) на доске и в тетрадях.

3. Устно решить № 67, 68.

4. Напишите два пятизначных числа:

а) кратных 3; б) кратных 2 и 3.

5. Решить № 82 и № 83 (на доске и в тетрадях).

Решение.

№ 82.

№ 83.

IV. Итог урока.

Как по записи натурального числа узнать, делится оно на 3 или не делится на 3?

Домашнее задание: выучить правила п. 3; решить № 87, № 90, № 91 (в; г).

Урок 1

Цели: ввести понятие простых и составных чисел; познакомить с таблицей простых чисел и научить учащихся использовать таблицу при выполнении заданий.

Ход урока

I. Устная работа.

1. Решить № 103 (1-е и 2-е задания каждого столбика).

2. Решить № 111.

3. Двое учащихся работают на доске: выполняют домашние задания № 90 и № 91 (в; г).

4. Вопросы: а) Какое число называют делителем данного натурального числа?

б) Какое число является делителем любого натурального числа?

II. Объяснение нового материала.

1. Найти делители чисел 7, 9 и 18.

2. Определение простого числа; определение составного числа. Привести примеры.

3. Число 1 не считают ни простым, ни составным.

4. Первыми десятью простыми числами являются 2, 3, 5, 7, 11, 13, 17, 19, 23, 29. Число 2 – наименьшее простое число. Это – единственное четное простое число, остальные простые числа нечетные.

5. Познакомить с таблицей простых чисел на форзаце учебника.

6. Любое составное число можно разложить на два множителя, каждый из которых больше 1. Простое число так разложить на множители нельзя.

III. Закрепление изученного материала.

1. Решить № 93 на доске и в тетрадях.

2. Устно решить № 94, 95, 96.

3. Разложить всеми возможными способами число 24:

а) на два множителя;

б) на три множителя;

в) на четыре множителя.

4. Решить № 107 (а, в) с комментированием.

5. Решить задачу.

Маша задумала число и сказала, что это число меньше 30; его называют, когда считают тройками и когда считают пятерками. Назовите это число.

Ответ: 15.

6. Известно, что число делится на 2, 3 и 5. На какие еще числа делится это число?

7. Придумайте несколько чисел, которые имеют только три делителя. Какую закономерность можно заметить?

IV. Итог урока.

Какие натуральные числа называют простыми? Какие натуральные числа называют составными? Почему число 1 не является ни простым, ни составным?

Домашнее задание: изучить п. 4; выучить правила; решить № 115, № 116, № 117.

Урок 2

Цели: выработать навыки и умения разложения чисел на множители; повторить понятие процента числа и нахождения дроби от числа; развивать логическое мышление учащихся.

Ход урока

I. Повторение изученного материала.

1. Устно решить № 103 (3-е и 4-е задания каждого столбика).

2. Что называется процентом? Как выразить в процентах числа?

3. Устно решить № 105 и № 106.

4. Решить устно № 104 (для а = 33).

II. Работа по учебнику.

1. Изучить по учебнику исторический материал «Решето» Эратосфена на страницах 33–34.

2. В настоящее время составление таблиц простых чисел можно «поручить» компьютерам, с их помощью уже получены огромные простые числа, которые «вручную», наверно, никогда бы не были найдены.

Однако компьютеры, даже и очень мощные, тоже имеют ограниченные возможности. И возникает такой естественный вопрос: можно ли построить, хотя бы в далеком будущем, такой мощный компьютер, чтобы он нашел, наконец, все простые числа? Оказывается, что ответ на этот вопрос уже есть и найден… больше двух тысяч лет назад. Мы уже прочитали, что великий математик Древней Греции Евклид доказал, что полный список составить просто невозможно. Можно сказать также, что среди простых чисел нет самого большого числа. Так две с лишним тысячи лет назад Евклид лишил математиков надежды получить когда-нибудь полный список простых чисел.

III. Выполнение тренировочных упражнений.

1. Устно решить № 98 и № 97.

2. Решить № 99 на доске и в тетрадях.

3. Самостоятельно решить № 100.

4. Устно решить № 101 и № 102.

5. Повторить признаки делимости на 2 и на 9.

Решить № 110 (б; г).

6. Повторить нахождение дроби от числа. Решить задачу № 113.

7. Решить № 108 на доске и в тетрадях.

IV. Итог урока.

1. Повторить определение простого и составного чисел.

2. Найдите два составных числа х, которые удовлетворяют неравенству 22 < x < 31.

3. Найдите два простых числа, каждое из которых больше 10 и меньше 20.

Домашнее задание: повторить п. 2 и 3; решить № 118, 119, 120.

рАЗЛОЖЕНИЕ НА ПРОСТЫЕ МНОЖИТЕЛИ

Урок 1

Цели: познакомить учащихся с разложением на простые множители числа; повторить признаки делимости чисел и научить использовать их при разложении чисел на простые множители.

Ход урока

I. Устные упражнения.

1. Решить № 125 (1-е и 2-е задания каждого столбика).

2. Устно решить № 126 и № 132 (а–в).

3. Изучением свойств простых чисел занимался русский математик Пафнутий Львович Чебышев. Он доказал, что между любым натуральным числом, большим 1, и числом, вдвое большим, всегда имеется не менее одного простого числа. Проверить это на примере нескольких чисел.

II. Изучение нового материала.

1. Задача. Нужно выделить участок земли прямоугольной формы площадью 18 м². Какими могут быть размеры этого участка, если они должны выражаться натуральными числами?

Решение.

1) 18 = 1 · 18; 2) 18 = 2 · 9; 3) 18 = 3 · 6.

Ответ: размеры участка могут быть: 1 м и 18 м; 2 м и 9 м; 3 м и 6 м.

Решая задачу, мы число 18 представили в виде произведения натуральных чисел. Говорят: разложили на множители. Если в разложении, например, числа 18 = 3 · 6 составной множитель 6 представить в виде произведения двух простых множителей 2 и 3, то тогда число 18 будет разложено на простые множители: 18 = 3 · 6 = = 3 · 2 · 3. Обычно записывают множители в порядке возрастания: 18 = 2 · 3 · 3.

2. Разложить (натуральное) число на простые множители – значит представить это число в виде произведения простых чисел.

3. Нередко для разложения натурального числа на простые множители сначала разлагают его в виде произведения составных множителей, а затем каждый из них разлагают на простые множители.

4. Прочитать по учебнику теоретический материал (п. 5) на с. 20–21.

5. Записать на доске и в тетрадях несколько первых простых чисел:

2; 3; 5; 7; 11; 13; 17; 19;…

Объяснение учителем разложения числа 3276 на простые множители (повторяются признаки делимости чисел на 2, на 3, на 5).



III. Закрепление изученного материала.

1. Разложить число на простые множители:

а) 16; б) 18; в) 15; г) 20; д) 72; е) 150.

2. Решить № 121 (а) на доске и в тетрадях.

3. Решить с комментированием № 122 (а).

4. Решить № 124 (а; б) с объяснением.

5. Повторение ранее изученного материала:

а) решить № 127 и 132 (г; д; е);

б) решить задачу № 133.

6*. Знаменитый ученый Христиан Гольдбах (1690–1764), работавший в Петербургской академии наук, высказал догадку (в 1742 г.), что любое натуральное число, большее 5, может быть представлено в виде суммы трех простых чисел. Проверить это на примере нескольких чисел.

IV. Итог урока.

Вопросы:

а) Существуют ли составные числа, которые нельзя разложить на простые множители?

б) Чем могут отличаться два разложения одного и того же числа на простые множители?

Домашнее задание: изучить п. 5; решить № 141 (а), № 142 (а; в), № 143, № 140 (устно).

Урок 2

Цели: выработать навык разложения чисел на простые множители; развивать логическое мышление учащихся.

Ход урока

I. Устная работа.

1. Решить № 125 (3-е и 4-е задания каждого столбика).

2. Решить № 126, 128 и 129.

3. Проверить выполнение учащимися домашнего задания:

а) устно № 140 по рисунку 6 учебника;

б) устно по тетрадям проверить № 142 (а; в);

в) на доске один учащийся записывает решение задачи № 143.

Решение.

Пусть первый тракторист вспахал х га земли, тогда второй вспахал 1,2х га.

Вместе они вспахали 12,32 га земли. Составим и решим уравнение:

х + 1,2х = 12,32

2,2х = 12,32

х = 12,32 : 2,2 = 123,2 : 22

х = 5,6.

Первый тракторист вспахал 5,6 га земли, второй вспахал 12,32 – 5,6 = 6,72 (га).

Ответ: 5,6 га; 6,72 га.

II. Выполнение упражнений.

1. Решить № 121 (б; в) на доске и в тетрадях.

Показать более простой способ разложения на простые множители чисел, оканчивающихся нулями: так как 10 т = 2 · 5, то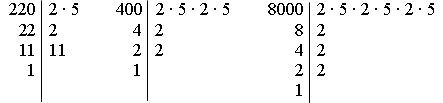



220 = 2² · 5 400 = 2² · 2² · 5² 8000 = 2⁶ · 5³

2. Решить № 122 (б) самостоятельно (с последующей проверкой).

3. Устно решить № 124 (в; г).

4. Решить № 123 с комментированием.

5. Повторение материала:

а) решить № 131.

Ответ:

б) решить № 135.

6. Самостоятельно решить № 139 (1; 3).

III. Итог урока.

Вопросы:

1) Что значит разложить число на простые множители?

2) Сформулировать признаки делимости на 2, на 5, на 10, на 3, на 9.

Домашнее задание: изучить п. 5; решить № 141 (б), № 142 (б), № 144 (а).
НОД. ВЗАИМНО ПРОСТЫЕ ЧИСЛА

Урок 1

Цели: ввести понятие наибольшего общего делителя и показать нахождение наибольшего общего делителя; дать определение взаимно простых чисел.

Ход урока

I. Устная работа.

1. Решить № 154 (а; б) и № 158.

2. Решить № 159.

II. Подготовка к изучению нового материала.

1. Решить № 160 с комментированием.

2. Решить № 157 (а) на доске и в тетрадях (вызвать к доске сразу трех учащихся).

3. Решить № 146 (а).

III. Изучение нового материала.

1. Разобрать решение задачи на с. 25 учебника.

2. Определение НОД (наибольшего общего делителя).

3. Определение взаимно простых чисел.

4. Правило нахождения наибольшего общего делителя нескольких натуральных чисел.

5. Иногда наибольшим общим делителем чисел является наименьшее из данных чисел. Например, для чисел 13, 26 и 39 наибольшим общим делителем будет число 13.

Просто определить наибольший общий делитель также, например, таких чисел 300, 500 и 700:

НОД (300; 500; 700) = 100.

IV. Закрепление нового материала.

1. Назовите два числа, для которых наибольшим делителем будет число: 9; 11; 13; 20; 25; 30.

2. Решить № 146 (б; в).

3. Устно решить № 144 (б).

4. Решить № 148 (а) с комментированием.

5. Решить № 149 (а; в) на доске и в тетрадях.

6. решить задачу:

Какое наибольшее число одинаковых подарков можно сделать из 320 орехов, 240 конфет и 200 шоколадок? Сколько конфет, орехов и шоколадок будет в каждом пакете?

Решение.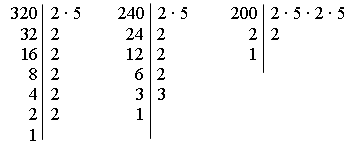



НОД (320; 240; 200) = 2 · 2 · 2 · 5 = 40.

Можно сделать 40 одинаковых подарков, в каждом пакете будет по 8 орехов; по 6 конфет, по 5 шоколадок.

7. Самостоятельно решить задачу № 138 (1).

V. Итог урока.

Вопросы:

1) Какое число называют наибольшим общим делителем двух натуральных чисел?

2) Какие два числа называют взаимно простыми?

3) Как найти наибольший общий делитель нескольких натуральных чисел?

Домашнее задание: выучить правила п. 6; решить № 169 (а), 170 (а), 173, 177.

Урок 2

Цели: отрабатывать навыки разложения чисел на простые множители и нахождения наибольшего общего делителя; закрепить знания и умения при нахождении дроби от числа.

Ход урока

I. Устная работа.

1. Решить № 154 (в; г; д).

2. Решить № 155, используя рисунок 7 учебника.

3. Какое число называют наибольшим общим делителем данных чисел?

Найдите наибольший общий делитель чисел: 1) 10 и 30; 2) 8 и 12; 3) 11 и 33; 4) 5 и 21; 5) 28 и 14; 6) 18; 27; 45; 7) 24; 36 и 48.

4. Какие два числа называют взаимно простыми? Найдите число, взаимно простое с числом: 6; 9; 15; 21; 25; 32; 40.

II. Выполнение упражнений.

1. Решить № 157 (б). Вызвать трех учеников к доске, каждый из них раскладывает одно из чисел на простые множители, остальные учащиеся в тетрадях раскладывают все данные числа на множители, а затем проверяют решение.

2. Решить задачу № 152 на доске и в тетрадях.

Решение.



3. Решить № 145 (б) с комментированием.

4. Решить № 148 (б; д) на доске и в тетрадях.

5. Решить № 147 (часть устно, некоторые письменно).

6. Повторение материала:

а) Решить задачу № 165 (1).

Решение.

1) 820 : 5 · 2 = 328 (м) отремонтировали во вторник;

2) 820 – 328 = 492 (м) осталось отремонтировать;

3) 492 : 3 · 2 = 328 (м) отремонтировали в среду;

4) 492 – 328 = 164 (м) отремонтировали в четверг.

Ответ: 164 м.

б) Решить № 166 и № 167.

III. Итог урока.

Доказать, что взаимно простые числа: 35 и 72; 27 и 28.

Домашнее задание: п. 6; решить № 169 (б); № 170 (б; в), № 175, 178 (б).

Урок 3

Цели: упражнять в нахождении наибольшего общего делителя; проверить знания учащихся и выявить пробелы; развивать логическое мышление учащихся.

Ход урока

I. Устная работа.

1. Решить № 159 и № 162.

2. Решить задачу:

Какое наибольшее число одинаковых комплектов можно составить из елочных игрушек, если имеется:

8 зайцев, 24 лисицы, 16 морковок и 48 яблок? По скольку зайцев, лисиц, морковок и яблок будет в каждом комплекте?

II. Выполнение упражнений.

1. Решить № 151 на с. 26 учебника.

Ответ:

2. Решить № 148 (г; е) на доске и в тетрадях.

3. Решить задачу № 153.

Решение.



Или можно решить по-другому:

1) 424 + 477 = 901 (человек) поехали за город.

2) 901 : 53 = 17 (автобусов) было выделено.

4. Решить № 157 (2) (коллективное решение, а затем полусамостоятельно в тетрадях записывают решение задачи).

III. Самостоятельная работа (10–15 мин).

Вариант I.

1. Найдите наибольший общий делитель чисел 7425 и 12375.

2. Запишите два простых числа у, которые удовлетворяют неравенству 17 < y < 24.

3. Докажите, что 209 и 171 не взаимно простые.

4. На станции стоят три пассажирских поезда: в первом – 418 мест в купейных вагонах, во втором – 494, а в третьем – 456. Сколько купейных вагонов в каждом поезде, если в каждом вагоне одинаковое число мест и их число больше 20?

Вариант II.

1. Найдите наибольший общий делитель чисел 1456 и 1560.

2. Запишите два простых числа у, которые удовлетворяют неравенству 19 < y < 30.

3. Докажите, что числа 299 и 184 не взаимно простые.

4. На нефтебазу прибыло три состава цистерн с нефтью: в первом составе было 360 т нефти, во втором – 432 т, а в третьем – 792 т. Сколько цистерн с нефтью было в каждом составе, если в каждой цистерне одинаковое число тонн нефти и это число больше 50?