Курсовая работа. Высшего профессионального образования мичуринский государственный аграрный университет
 Скачать 1.89 Mb.
|
5. СИНТЕЗ ПЛАНЕТАРНОГО РЕДУКТОРА.Планетарные редукторы, являясь передаточными механизмами, соединены последовательно с двигателем и рабочей машиной и служат для изменения частоты вращения и крутящего момента двигателя. Планетарные редукторы, как правило, проектируются соосными и многосателитными, что обеспечивает разгрузку центральных валов механизма от усилий. Такие конструкции компактны и удобны в сборке, бесшумны и надежны в работе. Основное преимущество планетарных редукторов заключается в том, что они позволяют осуществлять большое передаточное число (отношение) при меньших, чем у рядных механизмов габаритах и обладают достаточно высоким к.п.д. 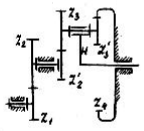 Рис. 5 – Схема редуктора  ; z1=11, z2=20, m=1, k=3.Формула передаточного числа планетарного механизма  Отношение  Дробь  представляем в виде простых сомножителей  Отношение  заменяем отношением  .Чтобы обеспечить условие соосности z3 + z2’ = z4 - z3’; необходимо ввести множители е1 и е2, т.е.  Принимаем  и  Тогда  Значит отношение Должно быть равно  Отсюда видно, что числа зубьев колес должны быть равны: 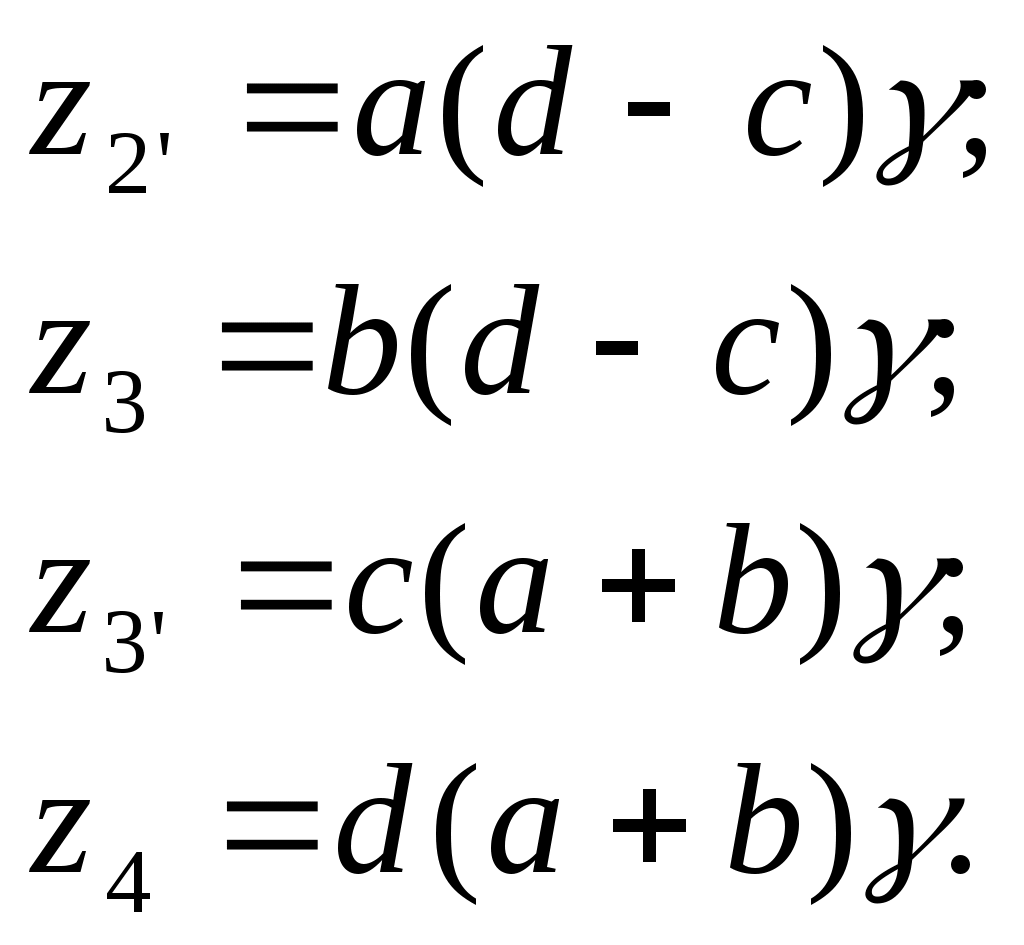 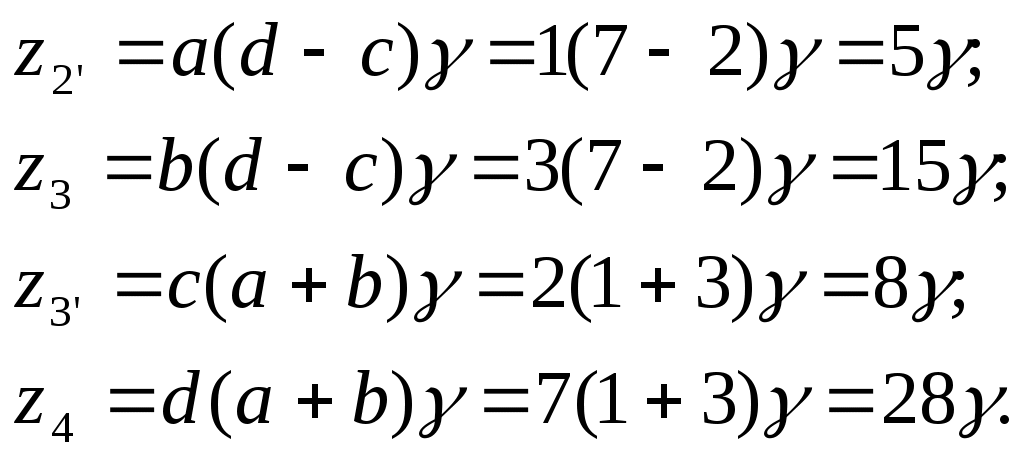 Тогда условие соосности z3 + z2’ = z4 - z3 или  Принимаем  Тогда Z2' =5∙4=20; z3 =15∙4=60; z3’ =8∙4=32; z4=28∙4=112 Проверяем  Условие соосности z3 + z2’ = z4 - z3 60+20=112-32 80=80 Условие соседства sin (1800/K) > (z3 + 2)/( z4 - z3'); (3.36) sin (1800/3) > (60+2)/(112-32) 0,589>0,775 Условие сборки  Не выполняется, принимаем k=2, тогда  - целое числоОпределим диаметры делительных окружностей колёс передачи.     Для построения прямой распределения скоростей точек звена необходимо знать скорости двух точек этого звена. Для звена I это точки 0 и А: ось 0 неподвижна и скорость её равна нулю. Скорость VA точки А изобразим вектором AaA произвольной длины, направленным перпендикулярно оси y . Прямая l , проведённая через точки 0 и a , образует с вертикальной осью y угол φH и является линией распределения скоростей точек колеса 1. Колесо 3 является неподвижным, следовательно, через точку С проходит ось мгновенного вращения сателлита 2. На колесе 2 известны скорости двух точек: А и С, поэтому линия l , проведённая через точки а и С, является прямой распределения скоростей для сателлита 2. Скорость VB оси В колеса 2 изображается вектором Вb. Соединив найденную точку b с точкой 0 получим прямую l , образующую с вертикальной осью у угол φ и являющуюся линией распределения скоростей для водила Н. Для построения плана угловых скоростей звеньев планетарной передачи построим прямоугольную систему координат х ,у с началом в точке Р. Отложим от точки Р на отрицательном участке оси у произвольное расстояние РК . Через точку К проведём две прямые линии под углами φ1 и φH к оси у . Точки пересечения этих прямых с осью х обозначим 1 и h соответственно. Угловые скорости колеса I и водила H определяются соотношениями:   Учитывая, что tgφ1 =P1/PK и tgφH =Ph/PK , получим выражение для передаточного отношения планетарной передачи  где PI и Ph - длины отрезков на плане угловых скоростей.  Относительная разница 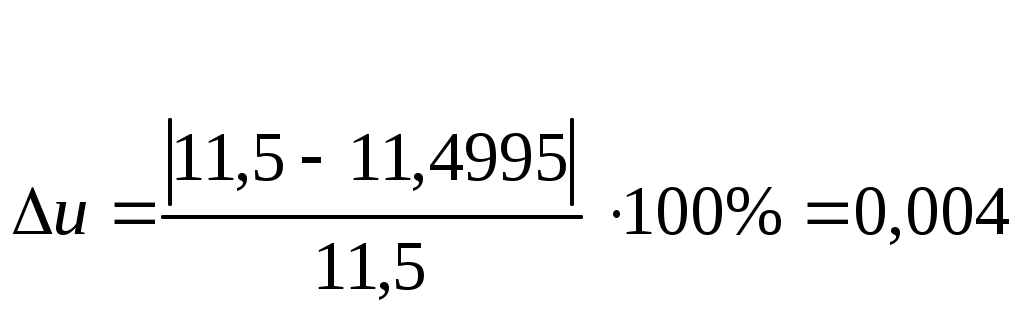 Величина Δu не превышает 5%, поэтому результаты вычислений и построений можно считать вполне удовлетворительными. |