Курсовая работа. Высшего профессионального образования мичуринский государственный аграрный университет

• Название: Высшего профессионального образования мичуринский государственный аграрный университет
• Дата: 16.09.2020
• Размер: 1.89 Mb.
• Имя файла: Курсовая работа.doc
• Тип: Документы; #138266
• страница: 4 из 12

1.5 Определение ускорений точек и угловых ускорений звеньев

Ведем расчет для 6-го положения.

Построение плана ускорений начинаем с точки А звена ОА. Абсолютное ускорение определяется из выражения:

.

(8)

Здесь нормальная составляющая направлена вдоль звена ОА к центру вращения (точке О) и равна по величине (для второго положения):

,

(9)

Тангенциальная составляющая равна 0, так как ₁=const и :

.

(10)

Второе звено совершает сложное движение, состоящее из вращательного относительно третьего звена и вращательного относительно первого звена. Составляем векторное уравнение для структурной группы 23:

(11)

В этом уравнении величины ускорений равны: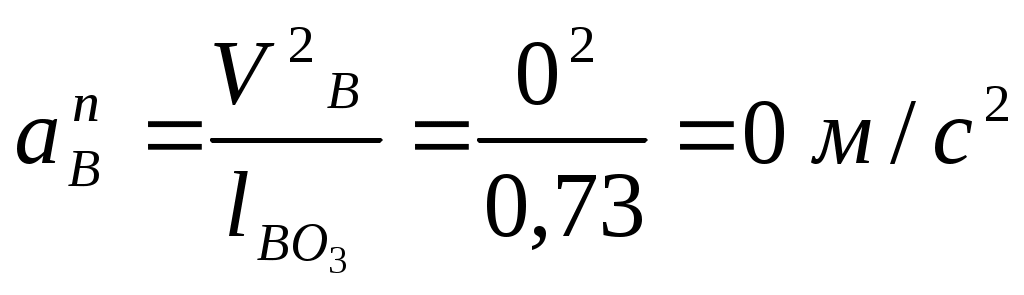



;



Примем масштабный коэффициент _а = 0,125 м/с²мм.

Решаем векторное уравнение (11) построением плана ускорений.

Из произвольной точки P – полюса плана ускорений, проводим вектор Pа параллельно звену ОА в направлении от точки А к точке О. Величина отрезка равна:

. (12)

Конец вектора обозначаем точкой а.

Из точки a в направлении от точки к точке А параллельно АB проводим вектор нормальной составляющей , конец вектора обозначаем буквой n₁. Величина отрезка равна:

.

Из точки n₁ проводим линию перпендикулярную звену АB.

Из полюса P проводим вектор ускорения . Направление ускорения параллельно звену ВС. Ускорение определяется отрезком:

.

Из точки n₂ проводим линию перпендикулярную звену BC до пересечения с линией проведенной из точки n₁. Точку пересечения обозначаем точкой b.

Определяем величины ускорений:

а_B = [Pb]_а = 126,70,125 = 15,8 м/с²;

= [n₂b]_а = 51,80, 125  = 6,5 м/с²;

= [ab]_а = 54,70, 125  = 6,8 м/с²;

= [bn₃]_а = 126,70, 125  = 15,8 м/с².

Определяем величину углового ускорения 2-го и3-го звена:

.

(13)

Ускорение точки С определяем из теоремы подобия.

АС/АВ=[ас]/ [аb]

[ас]= АС/АВ∙[аb] =279/80·43,75=12,55 мм

Отрезок [ас] откладываем под. углом 120º к отрезку [ab]

а_С= [рс]_а  =82,7·0,125=10,3 м/с.

Определим величины ускорений:

На плане механизма

АB/АS₂=4, АВ /ВS₂=1,3, ВО₃ /О₃S₃=3

Значит на плане ускорений тоже

[аs₂]=1/4[аb], [вs₂]=1/1,3[ав], [о₃s₃]=1/3[во₃]
 = [PS₂]_а = 98,80,125 = 12,35 м/с².

 = [PS₃]_а = 42,20,125 = 5,3 м/с².