Курсовая работа. Высшего профессионального образования мичуринский государственный аграрный университет

• Название: Высшего профессионального образования мичуринский государственный аграрный университет
• Дата: 16.09.2020
• Размер: 1.89 Mb.
• Имя файла: Курсовая работа.doc
• Тип: Документы; #138266
• страница: 8 из 12

3.5. Определение минимального радиуса кулачка.

Берем на плоскости произвольную т. О, откладываем от неё отрезок ОА, равный ходу h толкателя. Этот отрезок размечаем в соответствии с диаграммой . Через точки деления проводим перпендикуляры к линии ОА. От точек деления на перпендикулярах откладываем влево при подъеме и вправо при опускании толкателя отрезки, взятые из графика . Эти отрезки нужно откладывать в том масштабе, в котором отложен отрезок ОА, т.е. в масштабе . Соединяем плавной кривой концы этих отрезков и получаем кривую . Проводим под углом к горизонтали две касательные к построенной кривой. Эти прямые образуют в итоге область, в которой может располагаться центр кулачка. Выбираю длину отрезка BО равной r₀ = 62 мм на чертеже. Следовательно, минимальный теоретический радиус кулачка будет равен

,

(2.3)

где r_min – минимальный теоретический радиус кулачка, м;

μ_S – масштабный коэффициент, м/мм;

r₀ – минимальный радиус кулачка на чертеже, мм.

м.

3.6. Профилирование кулачка

Построения ведем в масштабе м/мм. Проведём окружность радиусом BA, полученным в предыдущем пункте. В произвольном месте окружности ОВ₀ выберем точку отсчета – т. В₀. Соединим точку В₀ с точкой О. От полученного луча в направлении (–ω) отложим угол φ_у, получим точку В₁₂. Дугу В₀В₁₂ разделим на 12 равных частей (получим точки В₁, В₂, В₃, …). Откладываем окружности, соответствующие перемещению толкателя в каждом из положений. Отмечаем точки пересечения отрезков ОВ0, ОВ1, ОВ2,… с соответствующими окружностями. Полученные точки соединяют плавной кривой – это профиль кулачка.

4 Расчет маховика

4.1 Построение графика приведенного к ведущему звену момента инерции механизма

4.1.1 За звено приведения принимаем кривошип 1. Полный приведенный момент инерции для каждого положения механизма определяется по формуле:

Jn = Jм + Jn + J0,

(4.1)

где J_м – приведенный момент инерции маховика;

J₀– приведенный момент инерции редуктора и кривошипа;

J_n – приведенный момент инерции звеньев механизма.

Приведенный момент инерции звеньев механизма определяем по формуле:

(4.2)

где mi – масса звена i; V_Si – скорость центра масс звена i; _i – угловая скорость звена i; ₁ – угловая скорость ведущего звена; Jsi – момент инерции звена i.

Для нашего рычажного механизма формула (4.2) примет вид:

,

(4.3)

при этом отношения скоростей зависят от положения механизма и определяются из планов скоростей.

Для 6-ого положения



Значения J_n для двенадцати положений кривошипа посчитаны с помощью ЭВМ, приведены в таблице 10.

4.1.2 Строим график J_n() приведенного момента инерции звеньев, приняв масштабные коэффициенты по осям:

_ = 0,0174 рад/мм, _J = 0,002 (кгм²)/мм.

Величину ординаты Y(J) найдем по формуле:

,

(4.4)

Например, для положения 6: .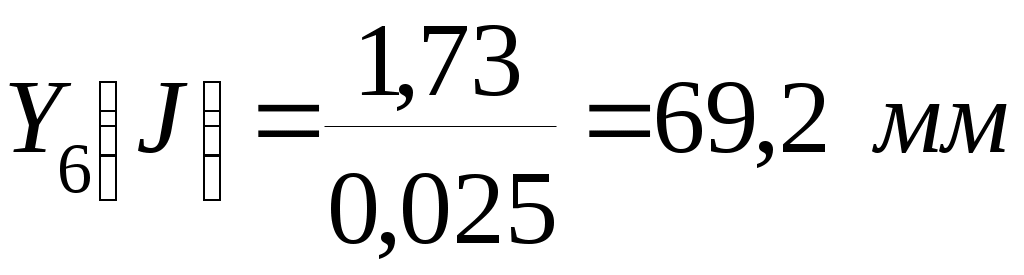

Значения остальных ординат, вычисленных аналогичным образом, занесем в таблицу 10.

Таблица 10 - Вычисленные значения

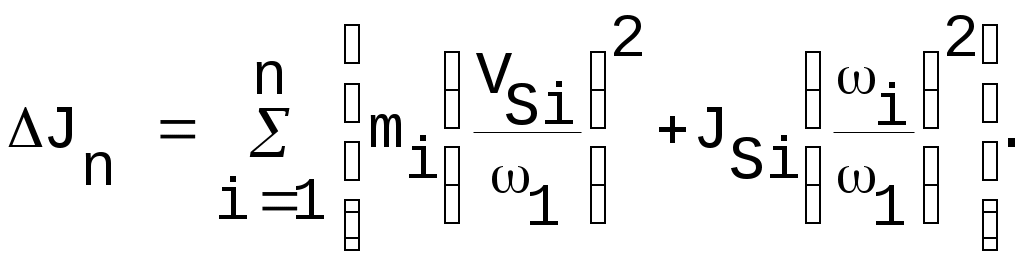
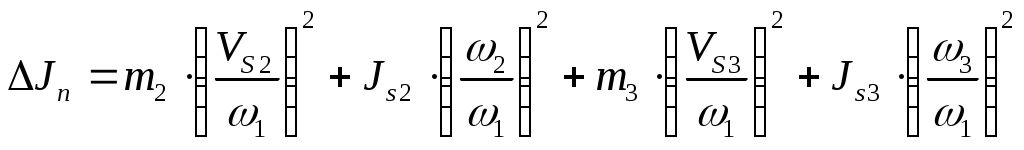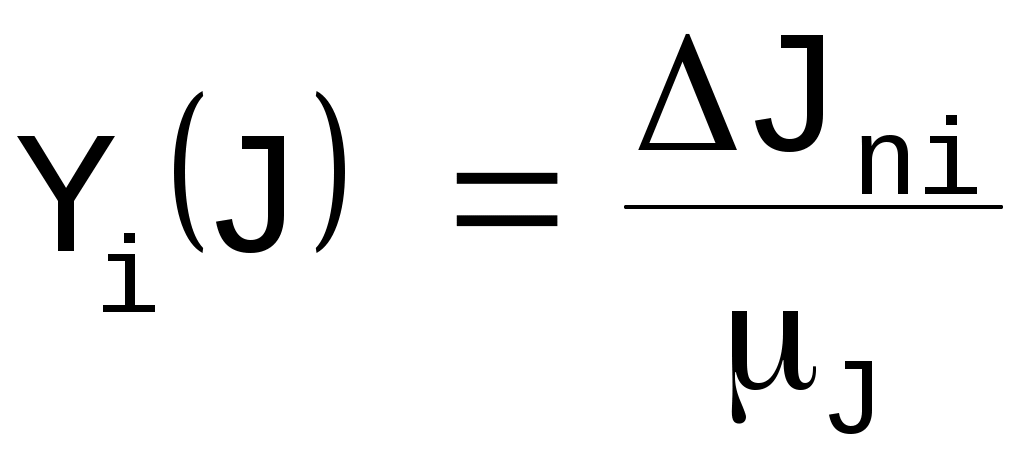№	Vs2	Vs3	∆Jn, кг·м2	У(Jn)-50, мм	РПС, Н∙м	Рn, Н·м	Мс, Н·м	У(Мс), мм
0	1,40	0,00	1,71	18,50	0	278,30	69,6	69,6
1	1,55	0,24	2,08	33,20	58	95,95	24,0	24,0
2	1,72	0,45	2,52	50,97	174	193,95	48,5	48,5
3	1,74	0,59	2,61	54,22	290	401,05	100,3	100,3
4	1,50	0,59	2,03	31,33	580	464,07	116,0	116,0
5	1,26	0,36	1,48	9,21	464	159,48	39,9	39,9
6	1,41	0,00	1,73	19,24	0	278,30	69,6	69,6
7	1,68	0,36	2,41	46,23	0	201,16	50,3	50,3
8	1,78	0,55	2,70	57,96	0	47,21	11,8	11,8
9	1,74	0,58	2,58	53,08	0	133,91	33,5	33,5
10	1,57	0,47	2,11	34,22	0	270,10	67,5	67,5
11	1,42	0,26	1,75	19,86	0	323,26	80,8	80,8