6. СИНТЕЗ ЭВОЛЬВЕНТНОЙ ЗУБЧАТОЙ ПЕРЕДАЧИ. 6.1. Анализ исходных данных.
Модуль зубчатых колёс: 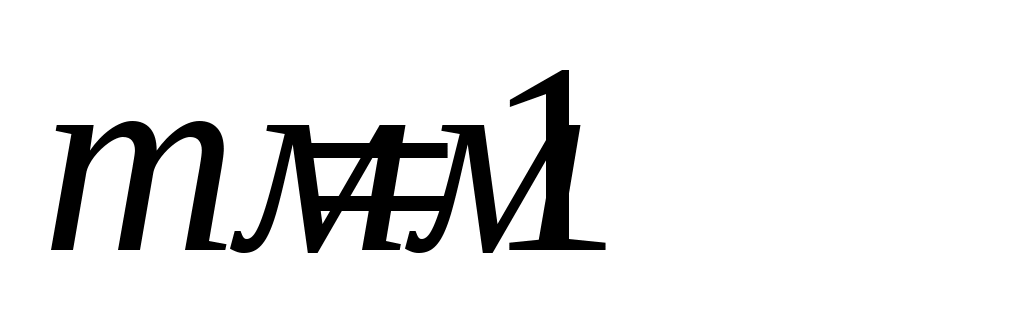 . .
Числа зубьев: 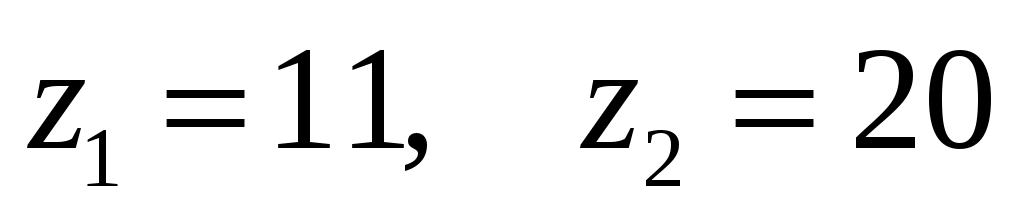 . .
Определяем передаточное число зацепления:
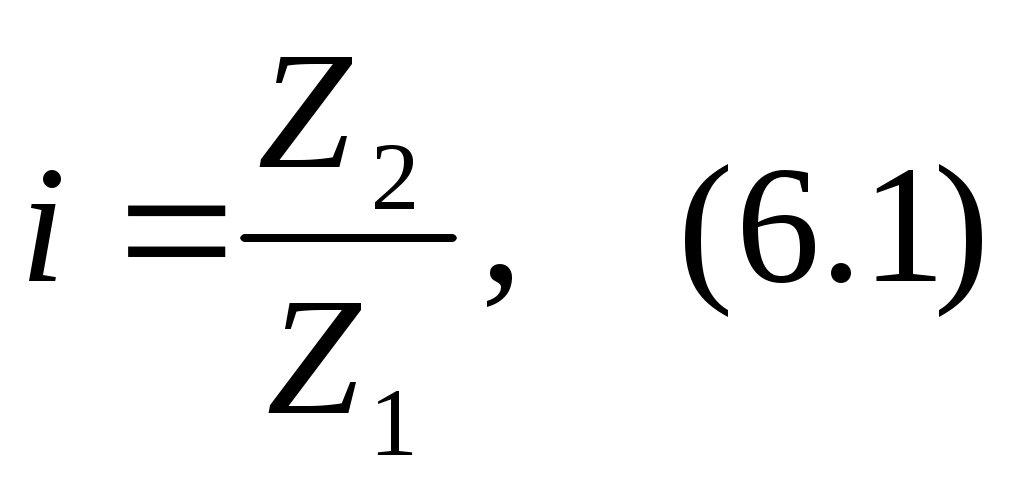
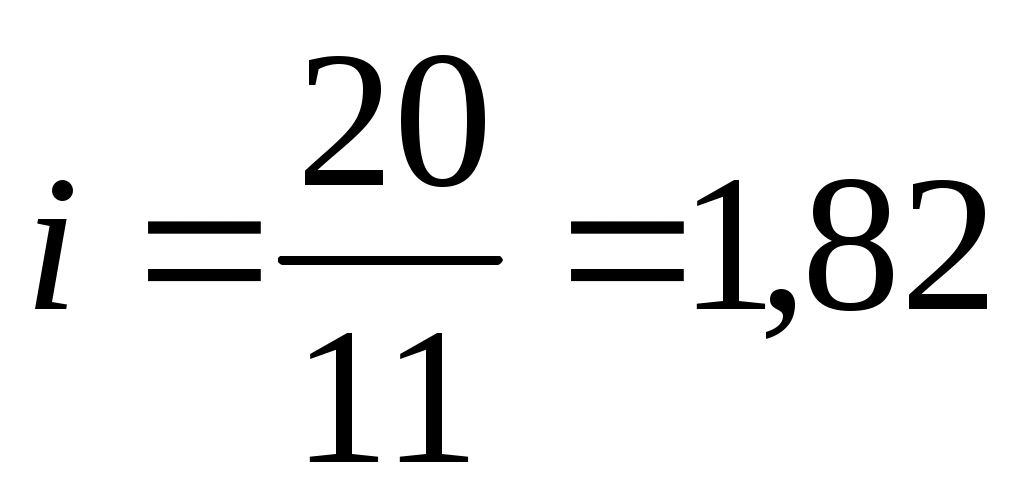
Выбираем коэффициенты смещения по табл.6 , в зависимости от числа зубьев соответствующего колеса.
Принимаем: X1 = 0,601, Х1 =0,303;
Профильный угол рейки α = 20 °, tg α =0,364.
Коэффициент высоты зуба рейки ha* =1.
Коэффициент радиального зазора С* = 0,25.
6.2. Геометрический расчёт эвольвентной зубчатой передачи.
Для вычисления угла зацепления зубчатой пары необходимо знать значения инволюты углов. Для определения этой тригонометрической функции имеются специальные таблицы, которые приведены в приложении
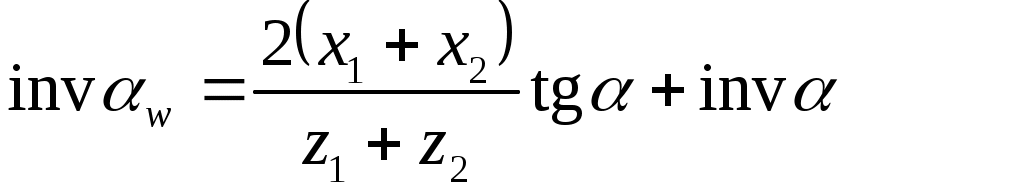 (6.2) (6.2)
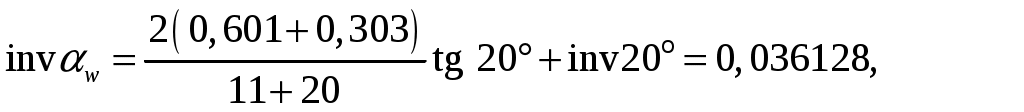
отсюда угол зацепления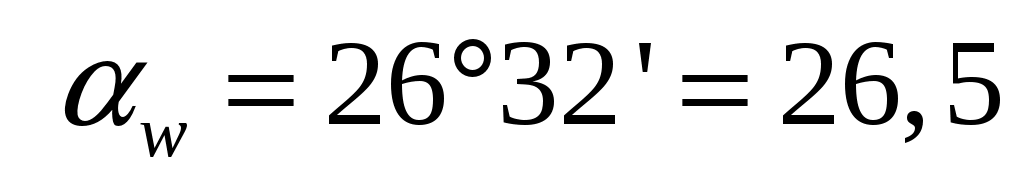 . .
Межосевое расстояние
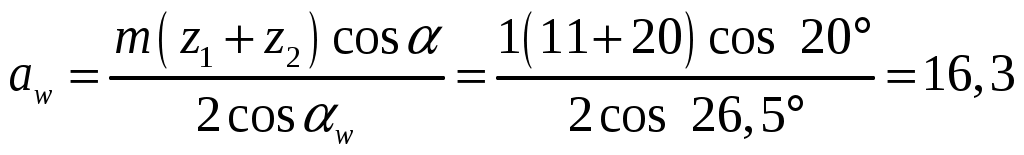 мм. мм.
Диаметры начальных окружностей:
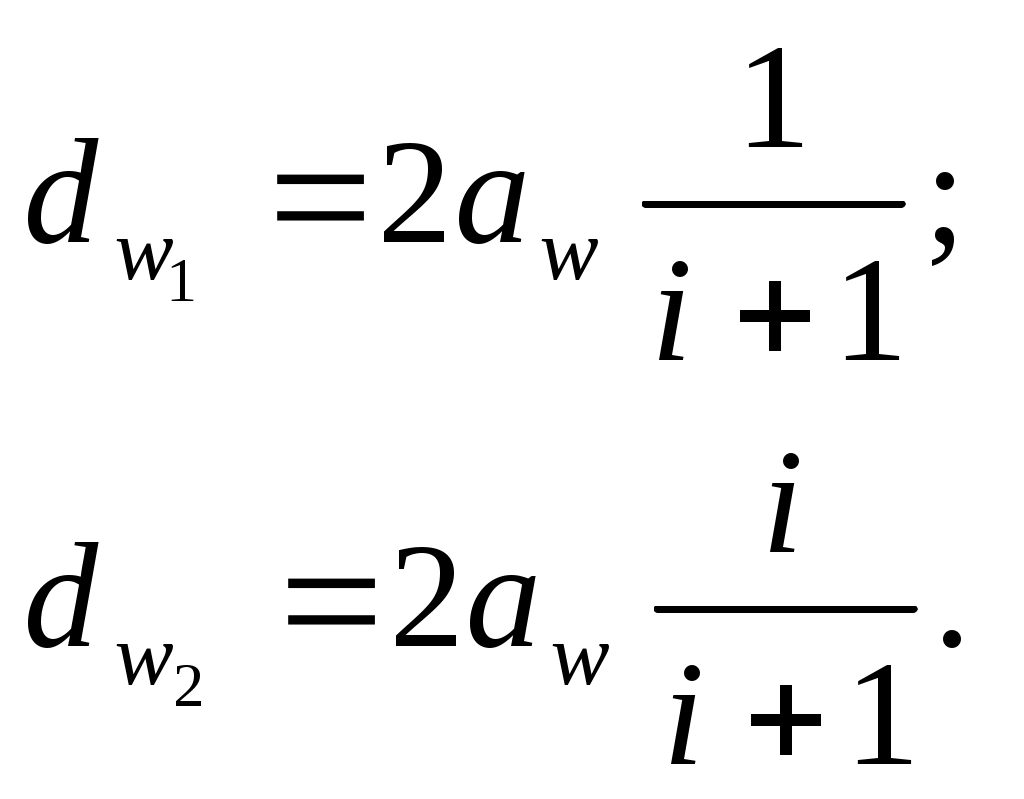 (6.4), (6.5) (6.4), (6.5)
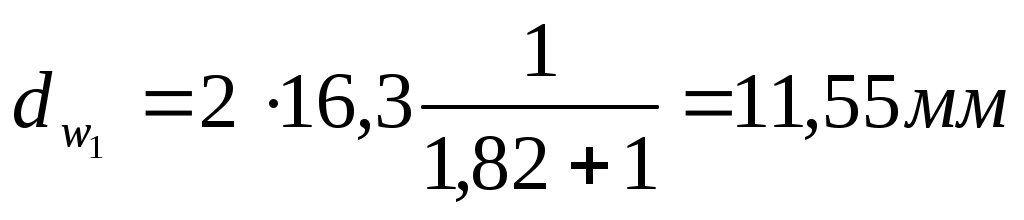
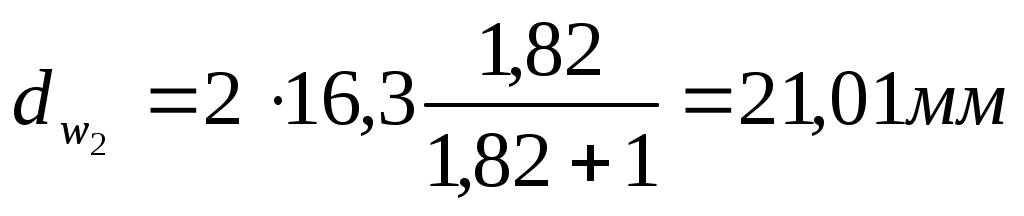
Диаметры делительных окружностей:
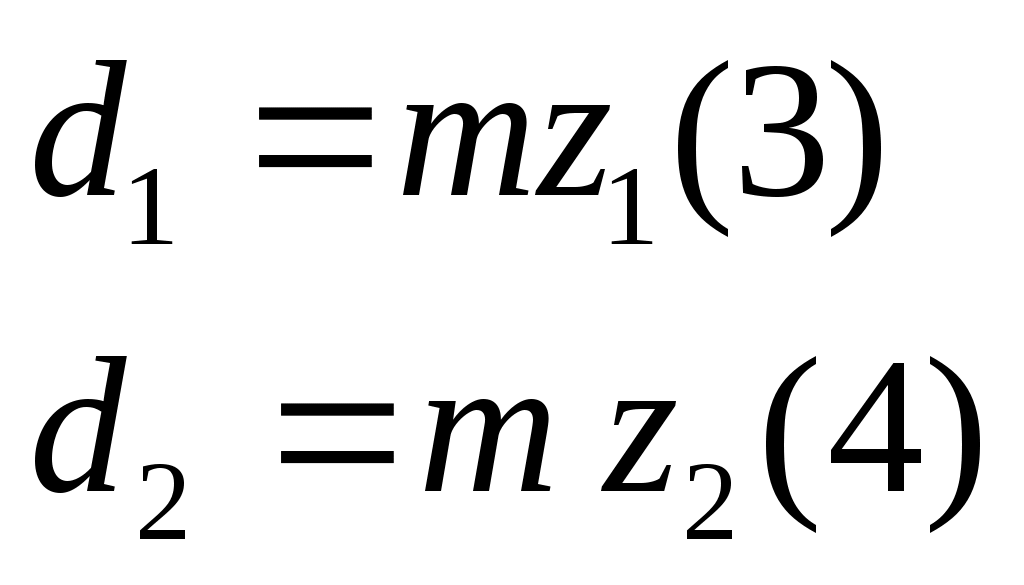 (6.6), (6.7) (6.6), (6.7)
Для шестерни: 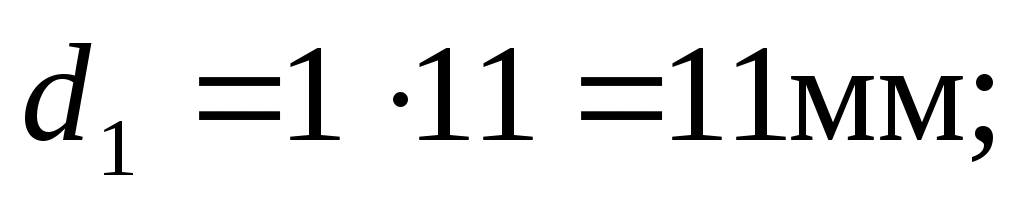
Для колеса: 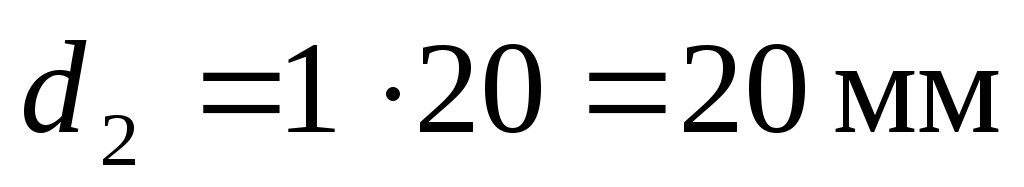
Определяем делительное межосевое расстояние, мм:
a = 0,5m(z1 +z2) (6.8)
a =0,5·1·(11+20)=15.5 мм
Определяем коэффициент воспринимаемого смещения:
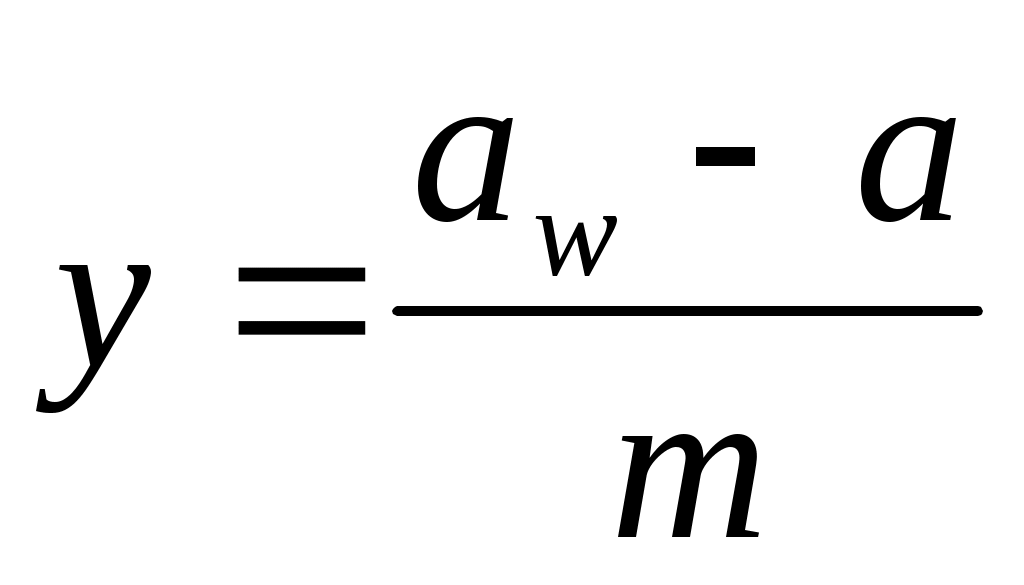 (6.9) (6.9)
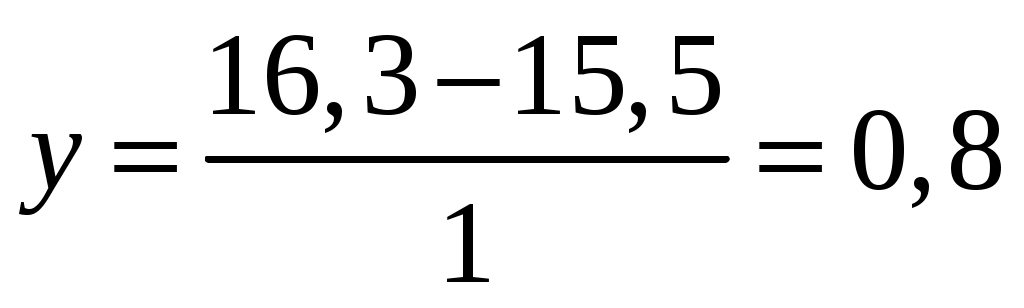
Определяем коэффициент уравнительного смещения:
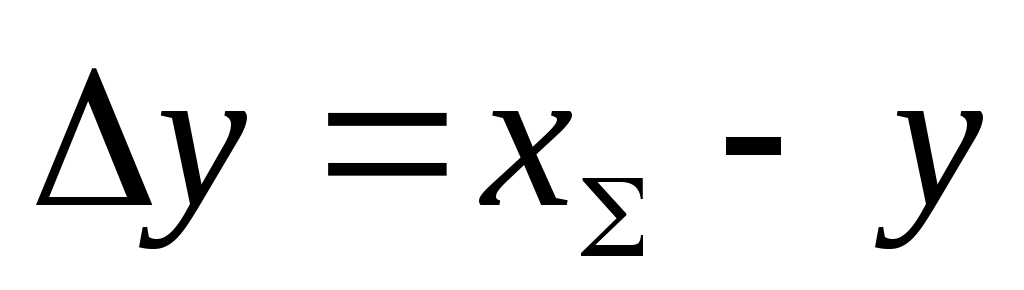 (6.10) (6.10)
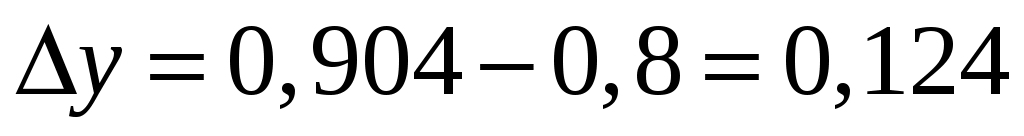
Определяем диаметры вершин зубьев колёс, мм:
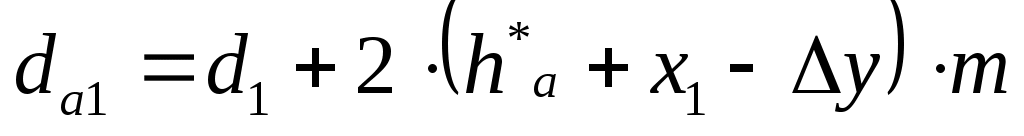 (6.11) (6.11)
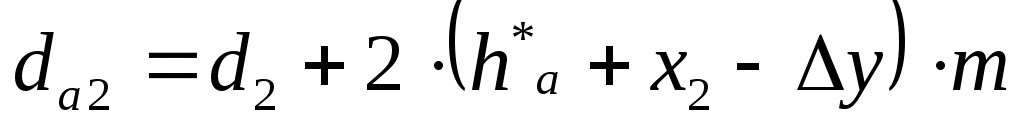 (6.12) (6.12)
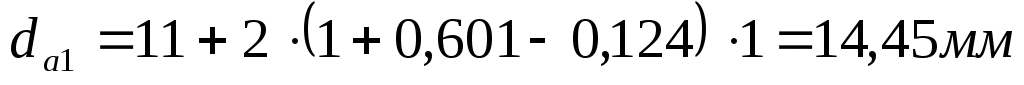
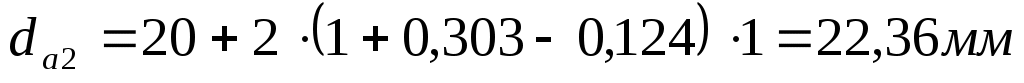
Определяем диаметры впадин зубьев колёс, мм:
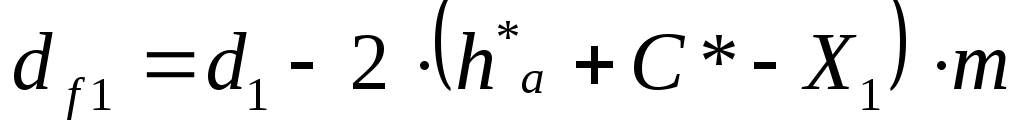 (6.13) (6.13)
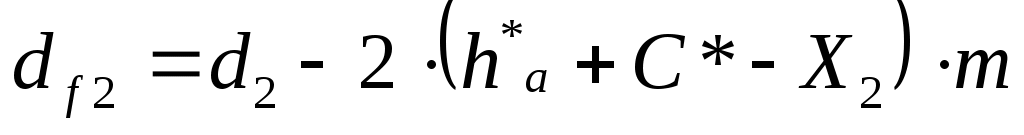 (6.14) (6.14)
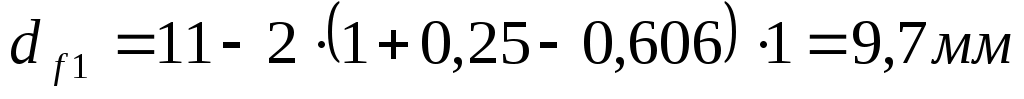
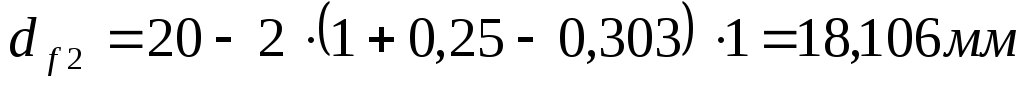
Определяем диаметры основных окружностей, мм:
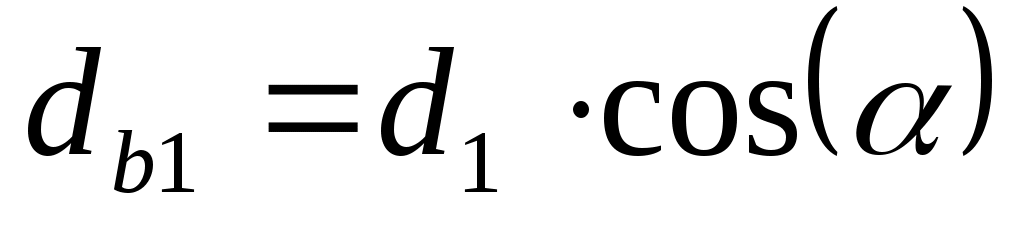 , (6.15) , (6.15)
|
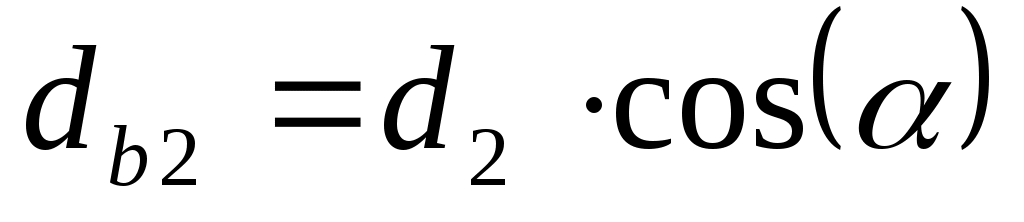 , (6.16) , (6.16)
|


Определяем шаг зубьев по делительной окружности, мм:
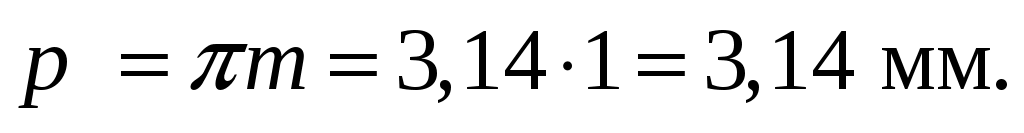 (6.17) (6.17)
Определяем шаг зубьев по начальной окружности, мм:
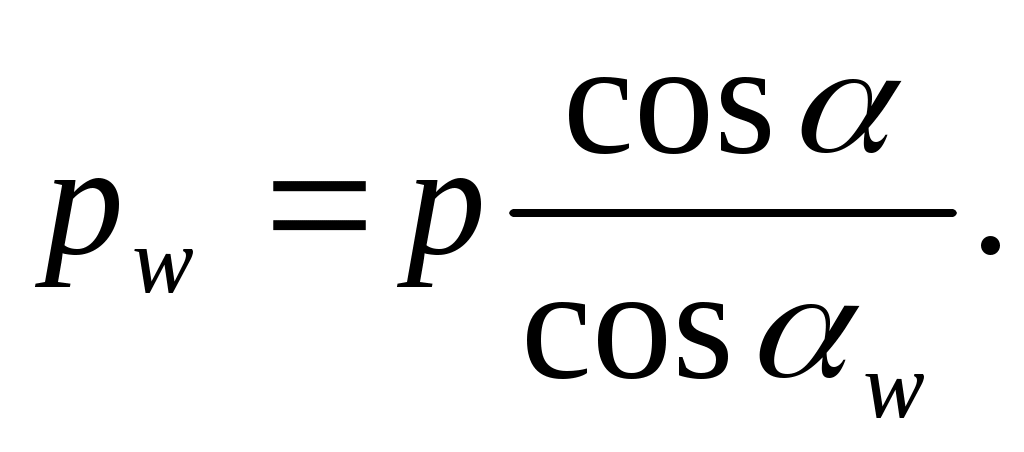 (6.18) (6.18)
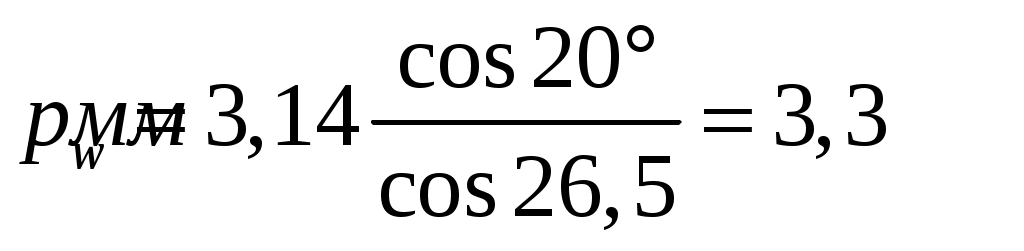
Определяем шаг зубьев по основной окружности, мм:
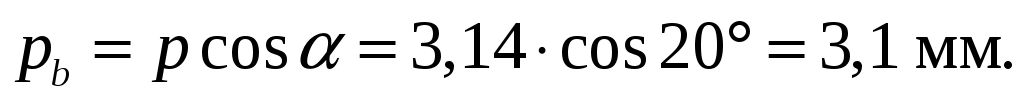 (6.19) (6.19)
Толщины зубьев по делительным окружностям колёс:
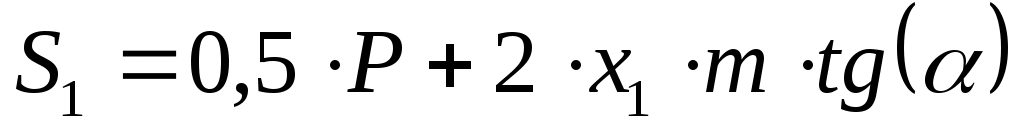 , (6.22) , (6.22)
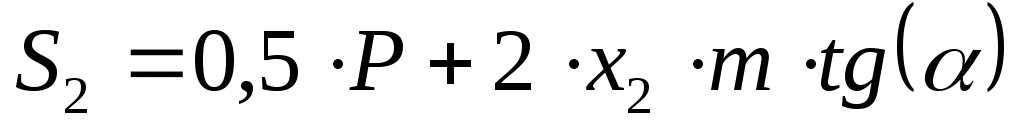 , (6.23) , (6.23)
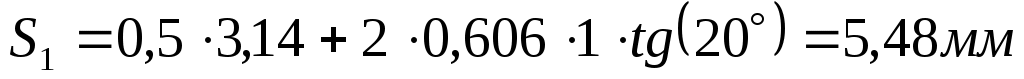 , ,
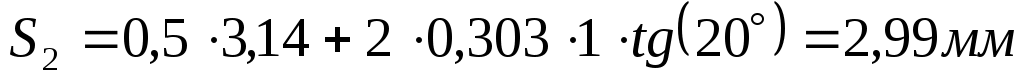
Определяем углы профилей на окружностях выступов зубьев:
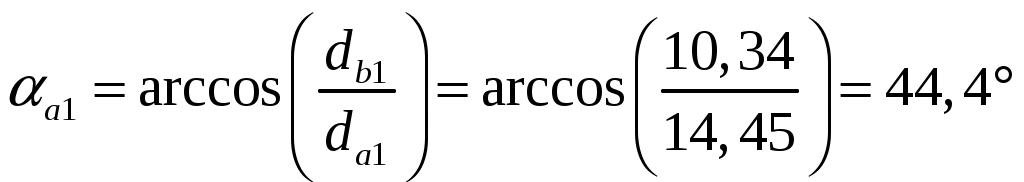 (6.26) (6.26)
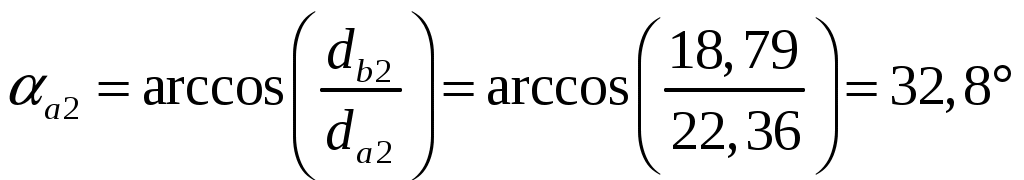 (6.27) (6.27)
(6.29)
Коэффициент перекрытия зубчатой передачи:
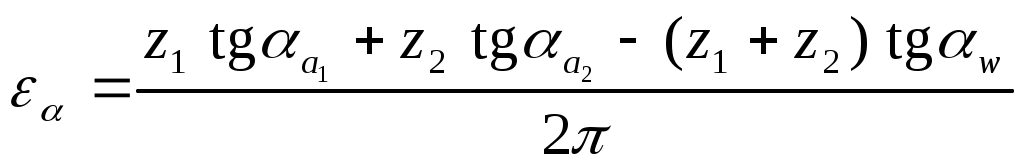 (63.30) (63.30)
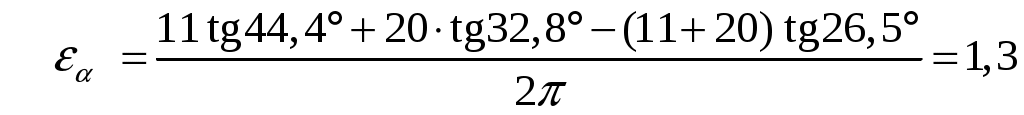
6.3. Построение графика удельного скольжения.
График строим в системе λOxk, в которой ось ординат проводим как продолжение линии O1N1, а ось абсцисс — параллельно линии зацепления N1N2. Обозначим абсциссу произвольной точки K на линии зацепления через xk. Тогда удельные скольжения будут равны
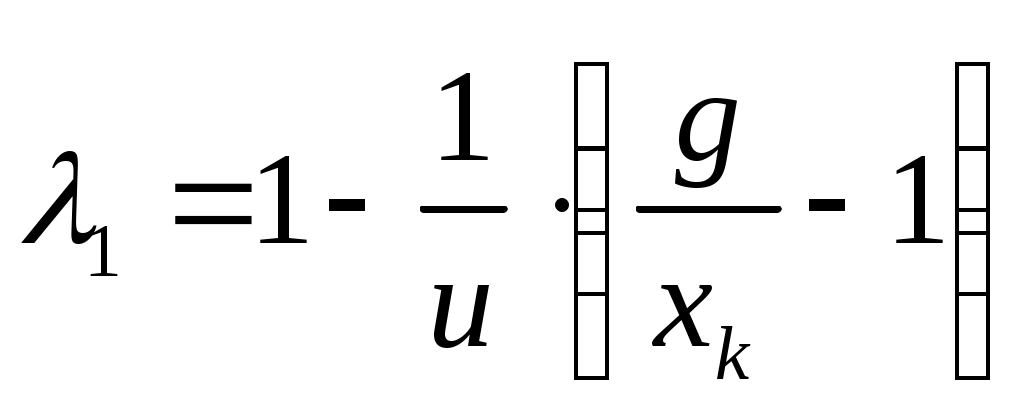 , , 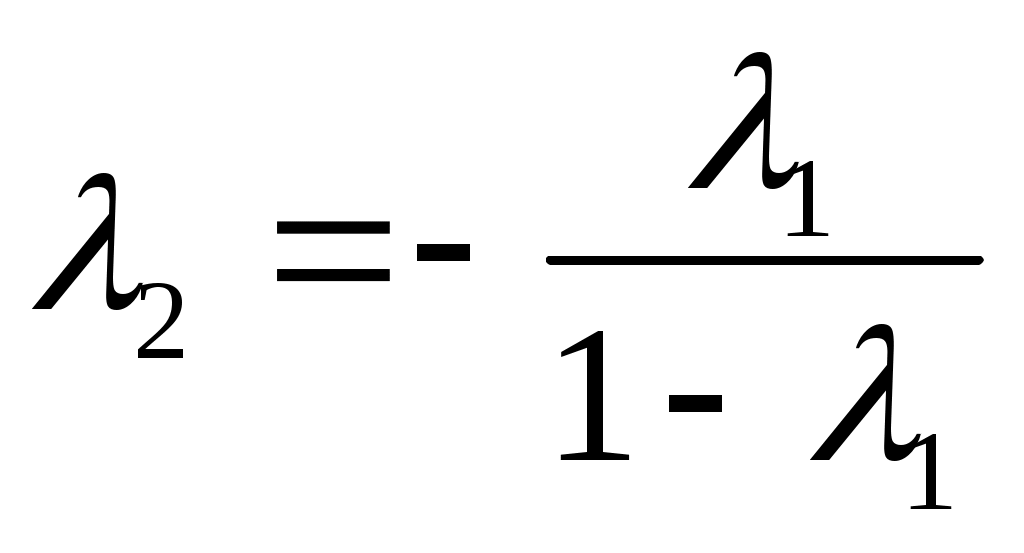 . .
Здесь
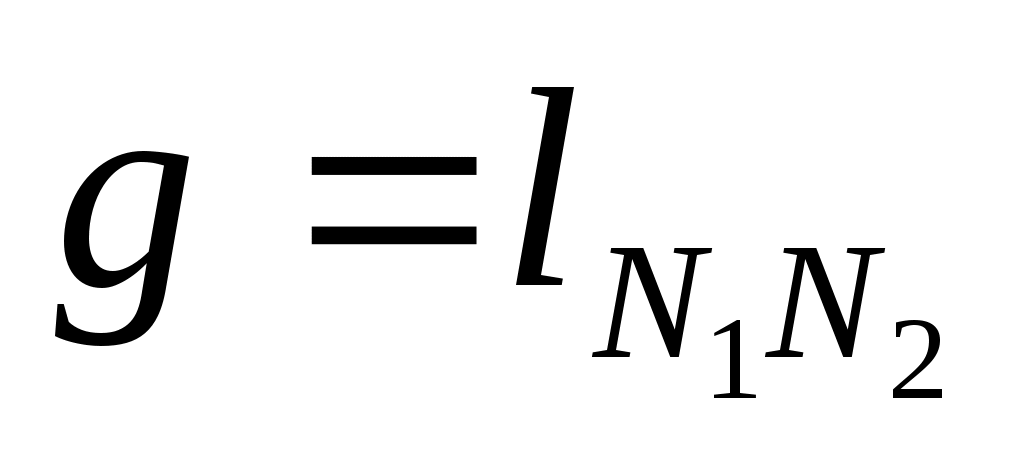 . .
Определив значения λ1 и λ2, строим их графики. При 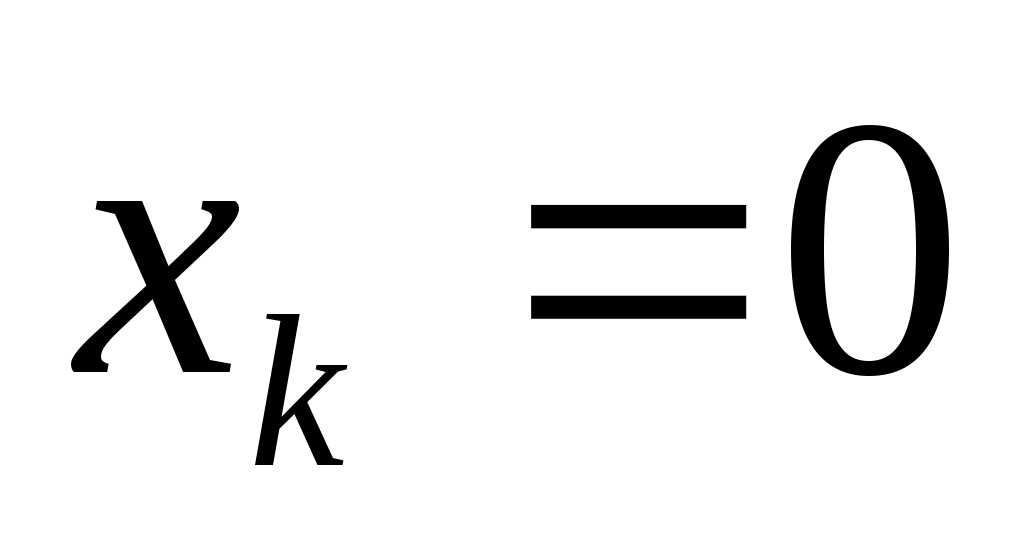 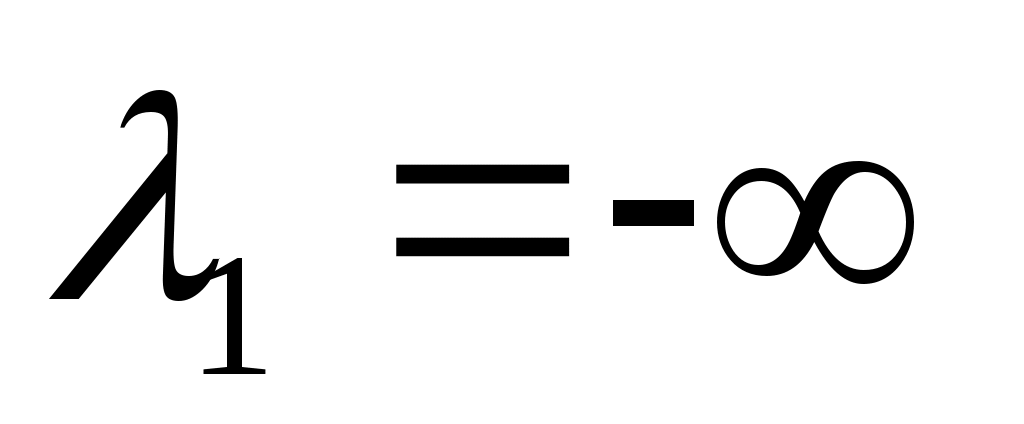 , , 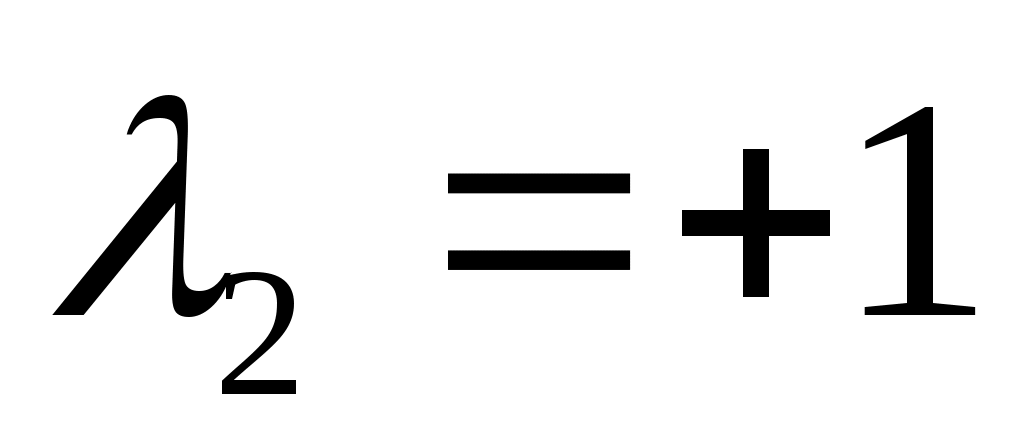 ; при ; при 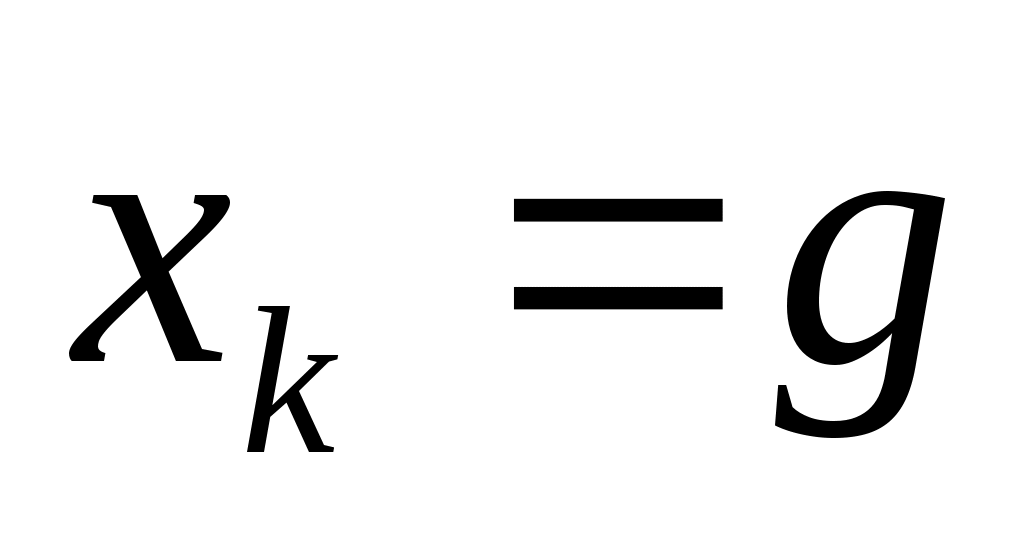 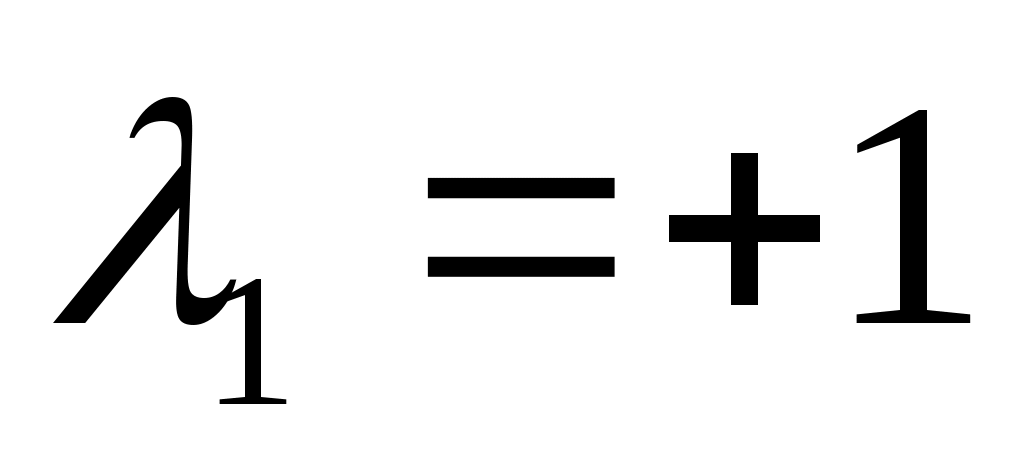 , , 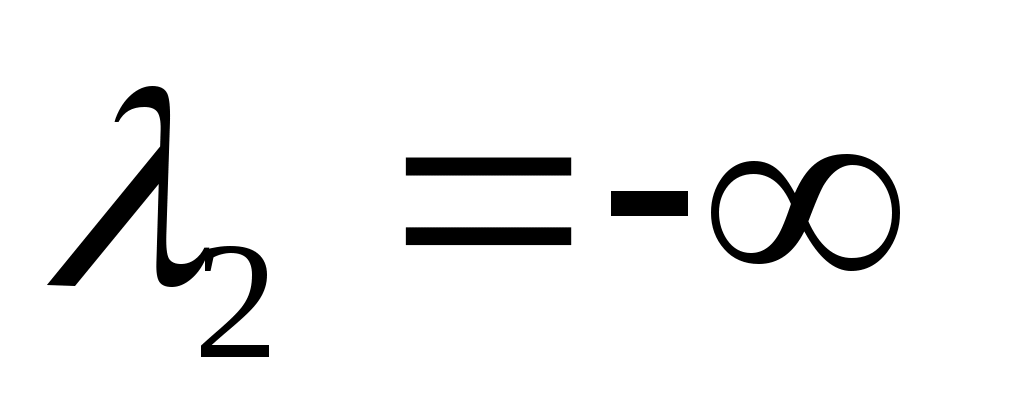 . .
6.4. Построение графика удельного давления.
График строим в системе λOxk, в которой ось ординат проводим как продолжение линии O1N1, а ось абсцисс — параллельно линии зацепления N1N2. Обозначим абсциссу произвольной точки K на линии зацепления через xk. Тогда удельные скольжения будут равны
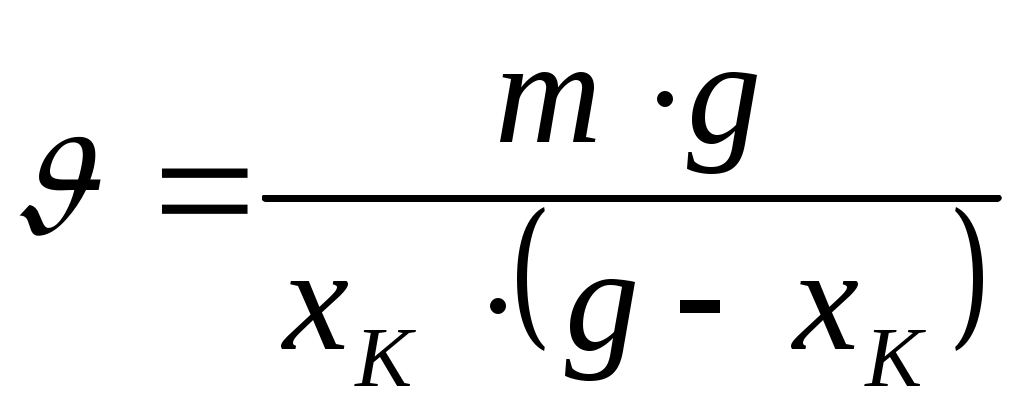 . .
Определив значения υ, строим его график. При 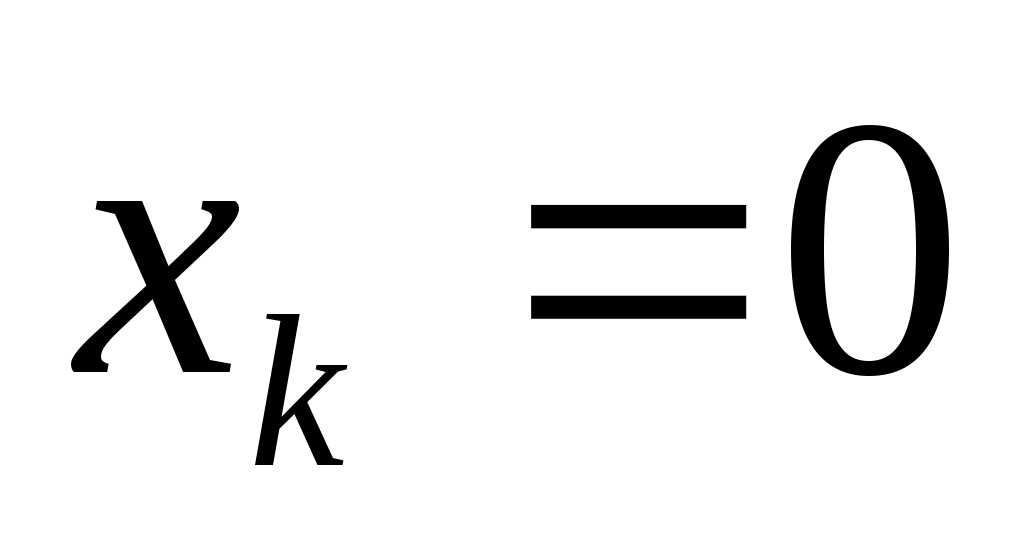 и и 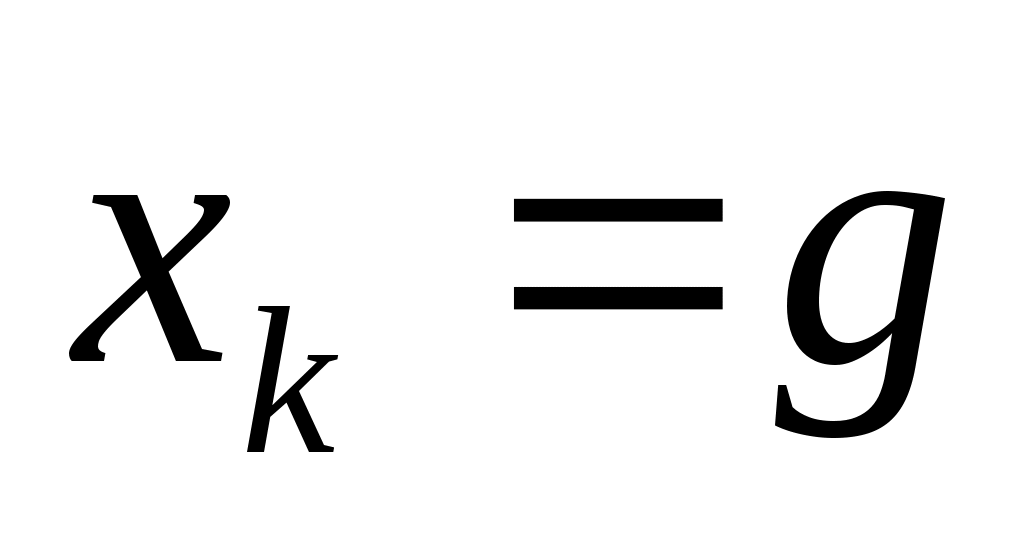 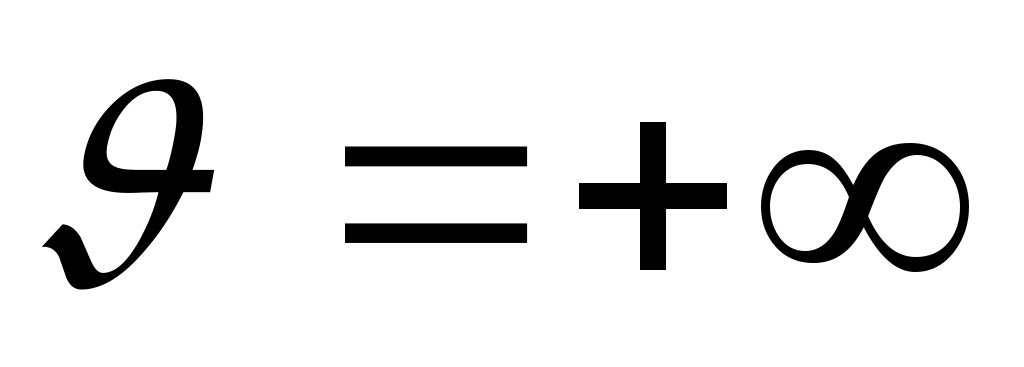 . .
ЗАКЛЮЧЕНИЕ
В ходе выполнения данного проекта были выполнены структурный и кинематический анализы рычажного механизма. Определены положения звеньев и построение траектории точек звеньев механизма, построены планы скоростей и ускорений.
В результате выполнения динамического синтеза рычажного механизма по коэффициенту неравномерности движения, были построены графики: приведённого к ведущему звену момента инерции механизма; приведенного момента сил сопротивления и движущих сил; работ сил сопротивления и движущих сил; изменений кинетической энергии механизма; диаграмма Виттенбауэра.
После определения момента инерции маховика, обоснованы его параметры.
В результате выполнения динамического анализа рычажного механизма определены следующие параметры: угловая скорость и угловое ускорение начального звена; инерционная нагрузка звеньев; реакции в кинематических парах структурных групп 4 – 5 и 2 – 3 без учета сил трения. Также выполнен кинематический расчет начального звена.
Полученные в ходе выполнения курсового проекта результаты могут служить основой для разработки технического проекта рычажного механизма.
Библиографический список
Теория механизмов и механика машин: Учеб для втузов/ К.В. Фролов, С.А. Попов, А.К. Мусатов и др. М: Высш.шк., 2001. – 496с.
Артоболевский ИИ. Теория механизмов и машин. М.: Наука, 1975.
Лачуга Ю.Ф., Воскресенский А.Н., Чернов М.Ю. Теория механизмов и машин. Кинематика, динамика и расчет. М.: Колос, 2006. – 304с., ил. – (Учебники и учебные пособия для студентов высших учебных заведений).
Кореняко А.С. Курсовое проектирование по теории механизмов и машин. М., 1970.
Левитский Н.И. Теория механизмов и машин. М.: Наука, 1990. – 590с.
Попов С.А., Тимофеев Г.А. Курсовое проектирование по теории механизмов и механике машин. М.: Высш.шк., 2002. – 408с.
Юдин В.А., Петрокас Л.В. Теория механизмов и машин. М., 1977.
|
 Скачать 1.89 Mb.
Скачать 1.89 Mb.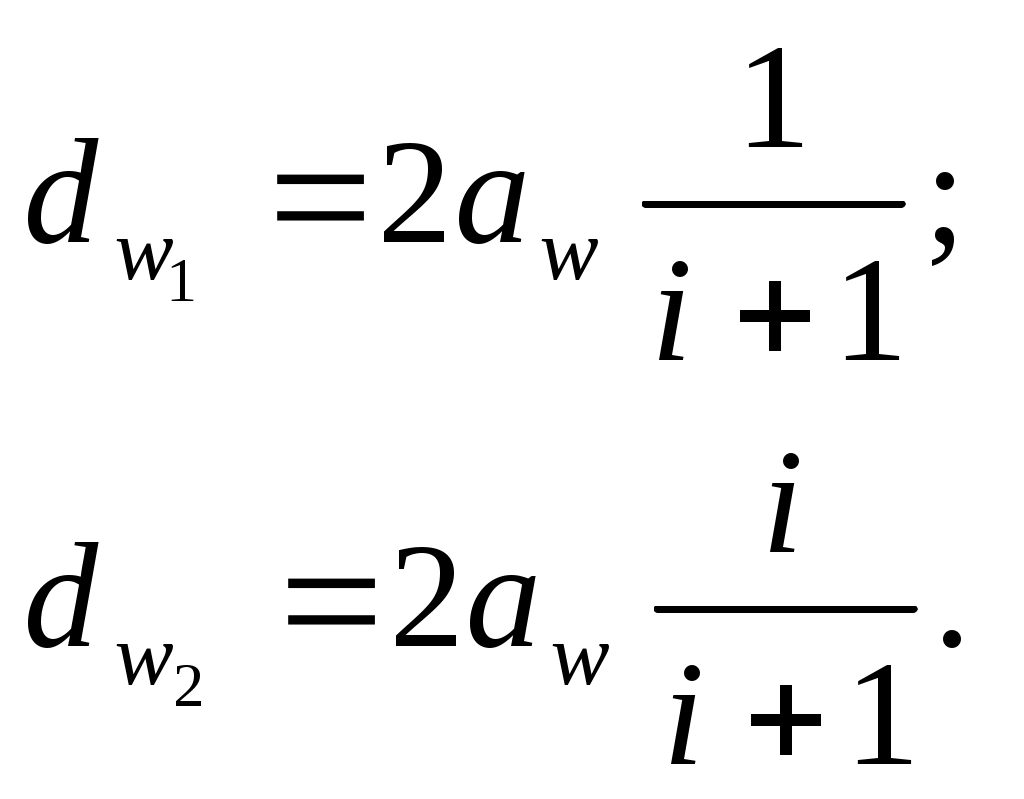 (6.4), (6.5)
(6.4), (6.5)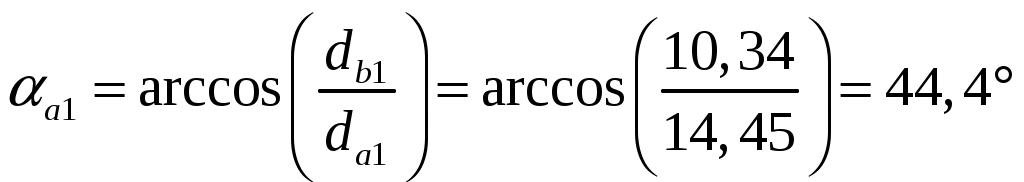 (6.26)
(6.26)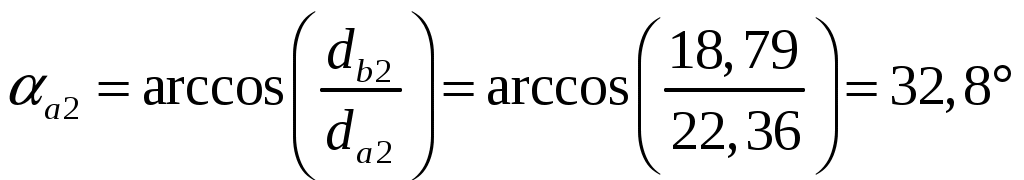 (6.27)
(6.27)
