Вопрос Пусть y

• Название: Вопрос Пусть y
• Дата: 04.03.2018
• Размер: 0.76 Mb.
• Имя файла: Test_RAVANDA_2.docx
• Тип: Документы; #37687
• страница: 7 из 8

 

Решение:
Исследования остатков e_i предполагают проверку пяти предпосылок метода наименьших квадратов:
1) случайный характер остатков;
2) нулевая средняя величина остатков, не зависящая от x_i; 
3) гомоскедастичность остатков – дисперсия каждого отклонения e_i одинакова для всех значений x_i;
4) отсутствие автокорреляции остатков (значения остатков e_i распределены независимо друг от друга);
5) остатки подчиняются нормальному закону распределения.
В данном случае очевидно выполнение предпосылки о случайном характере остатков, на графике в расположении остатков нет направленности, они расположены в форме облака, значит, предпосылка о случайном характере остатков выполняется.
Остатки колеблются около нуля, следовательно, предпосылка о нулевой средней величине остатков также выполняется.
Гомоскедастичность остатков означает, что дисперсия остатков не зависит от независимой переменной. В данном случае, согласно анализу графика остатков, это не так. При небольших значениях x_i величины остатков невелики, при увеличении значений x_i величины остатков также увеличиваются, то есть предпосылка о гомоскедастичности остатков нарушается.
Предпосылки о гетероскедастичности остатков просто не существует.

 

Кейс 1, задача 3
По 72 банкам построено уравнение зависимости размеров кредитов, выданных предприятиям и организациям, в млн. руб. (y) от собственного капитала, млн руб. (x): y = 710,967 + 3,057 ∙ x . Исходные данные упорядочены по убыванию величины собственного капитала. По величинам остатков рассчитан коэффициент автокорреляции первого порядка, равный -0,45539. На рисунке представлен график остатков.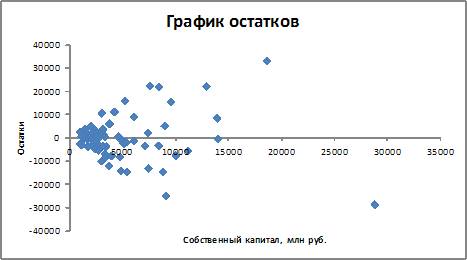


Если для остатков модели, выполнены предпосылки МНК, то оценки параметров, полученные методом наименьших квадратов (МНК), обладают свойствами …

			несмещенности
			состоятельности
			эффективности
			гомоскедастичности
			гетероскедастичности
			нормального распределения

 

Решение:
Оценки параметров регрессии должны обладать определенными критериями: быть несмещенными, состоятельными и эффективными. Несмещенность оценки означает, что математическое ожидание остатков равно нулю. Оценки считаются эффективными, если они характеризуются наименьшей дисперсией. Состоятельность оценок характеризует увеличение точности оценок с увеличением объема выборки. Если выполняются следующие предпосылки метода наименьших квадратов:
1) случайный характер остатков;
2) нулевая средняя величина остатков, не зависящая от x_i; 
3) гомоскедастичность остатков – дисперсия каждого отклонения e_i одинакова для всех значений x_i; 
4) отсутствие автокорреляции остатков (значения остатков e_i распределены независимо друг от друга);
5) остатки подчиняются нормальному закону распределения, 
то оценки, полученные методом наименьших квадратов, обладают свойствами несмещенности, состоятельности и эффективности.

 


Кейс 1, задача 4
По 72 банкам построено уравнение зависимости размеров кредитов, выданных предприятиям и организациям, в млн. руб. (y) от собственного капитала, млн руб. (x): y = 710,967 + 3,057 ∙ x . Исходные данные упорядочены по убыванию величины собственного капитала. По величинам остатков рассчитан коэффициент автокорреляции первого порядка, равный -0,45539. На рисунке представлен график остатков.


Значение критерия Дарбина–Уотсона составит … (Полученное значение округлите до десятых.)

Ответ: 2,9

 

Решение:
Статистика Дарбина–Уотсона вычисляется по формуле  , где  – коэффициент автокорреляции первого порядка. Поскольку  = –0,45539, то статистика Дарбина–Уотсона d = 2 · (1 - (-0,45539)) = 2,9.

 


Кейс 2, задача 1
Динамика показателя среднего размера назначенных пенсий в России в период 2005–2011 гг. характеризуется данными, представленными на графике.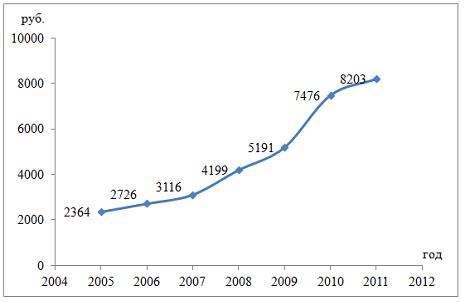


Функция, описывающая зависимость между порядком коэффициента автокорреляции и его значением, называется …

			автокорреляционной
			аппроксимирующей
			сглаженной
			структурной

 

Решение:
Функция, описывающая зависимость между порядком коэффициента автокорреляции и его значением, называется автокорреляционной функцией.

Кейс 2, задача 2

Динамика показателя среднего размера назначенных пенсий в России в период 2005–2011 гг. характеризуется данными, представленными на графике.


Установите соответствие между порядком коэффициента автокорреляции и его значением.

1. Коэффициент автокорреляции первого порядка

2. Коэффициент автокорреляции второго порядка

3. Коэффициент автокорреляции третьего порядка

1. 0,95603

2. 0,97694

3. 0,90784

Кейс 2, задача 3

Динамика показателя среднего размера назначенных пенсий в России в период 2005–2011 гг. характеризуется данными, представленными на графике.


Значение среднего размера назначенных пенсий в России в 2012 г., рассчитанное на основе линейного тренда, составит _____ руб. (Полученное значение округлите до целых.)

Ответ: 8910

.

Кейс 3, задача 1

По обследованию 12 случайно выбранных семей характеристики показателей накоплений, дохода и имущества представлены в таблице.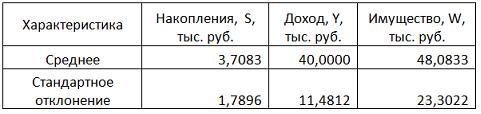


Построена матрица парных коэффициентов корреляции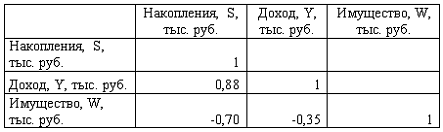


Тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии, характеризует …

Ответ: частный коэффициент корреляции

Кейс 3, задача 2

По обследованию 12 случайно выбранных семей характеристики показателей накоплений, дохода и имущества представлены в таблице.


Построена матрица парных коэффициентов корреляции


Для сравнительной оценки влияния факторов на результат используются такие показатели, как …

коэффициенты эластичности

стандартизированные коэффициенты регрессии

Кейс 3, задача 3

По обследованию 12 случайно выбранных семей характеристики показателей накоплений, дохода и имущества представлены в таблице.


Построена матрица парных коэффициентов корреляции


На основании сравнения частных F-критериев Фишера (Fтабл=5,12) можно утверждать, что фактор …

 х1целесообразно включать в уравнения регрессии после того, как в него был включен факторх2

Кейс 3, задача 4

По обследованию 12 случайно выбранных семей характеристики показателей накоплений, дохода и имущества представлены в таблице.


Построена матрица парных коэффициентов корреляции


Свободный член уравнения в естественной форме равен … (Полученный ответ округлите до сотых.)

Ответ: 0,75.

Решение:

Сначала найдем уравнение регрессии в стандартизированном виде. Будем считать х1– доход,х2– имущество. Коэффициенты парной корреляции известны и равны,,.
Расчет стандартизированных коэффициентов выполним по формулам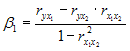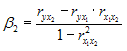
==0,7236;
==-0,4467.
Для построения уравнения в естественной форме воспользуемся формулой.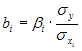

Итак, ;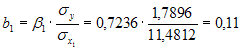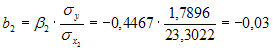


По формулерассчитаем свободный член уравнения в естественной форме.

= 3,7083 - 0,11 · 40 - ( -0,03)·48,0833=0,75.

Кейс 4, задача 1

В таблице представлены данные по субъектам федерации Центрального федерального округа, за исключением Москвы. Области упорядочены по возрастанию независимой переменной х– объему кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам.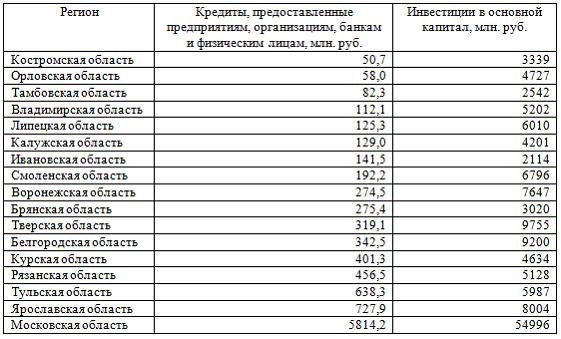


По данной выборке построено уравнение регрессии y = 3151,1 + 8,8487 · x. Коэффициент детерминации R2= 0,9708.

Средняя ошибка аппроксимации по уравнению регрессии, построенному по всей выборке, равна ____ %. (Полученное значение округлите до целых.)

Ответ: 36

Кейс 4, задача 2

 В таблице представлены данные по субъектам федерации Центрального федерального округа, за исключением Москвы. Области упорядочены по возрастанию независимой переменной х– объему кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам.


По данной выборке построено уравнение регрессии y = 3151,1 + 8,8487 · x. Коэффициент детерминации R²= 0,9708.

Верными относительно полученного уравнения регрессии и коэффициента детерминации утверждениями, которые учитывают характер выборки, являются …

высокое значение коэффициента детерминации определяется наличием в выборке аномальных значений

полученное уравнение не рекомендуется использовать для прогнозирования

 высокое значение коэффициента детерминации говорит о том, что между объемом кредитов и объемом инвестиций в основной капитал существует тесная линейная зависимость

полученное уравнение имеет высокую прогнозную силу

Решение:

Данные упорядочены по возрастанию объемов кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам. Даже беглый взгляд на данные позволяет заметить, что Московская область является аномальным значением – в ней обе переменные имеют значения, в разы превосходящие все остальные величины. Такие значения называются аномальными, или выбросами. На рисунке показано расположение точек всей выборки и уравнение регрессии, построенное по ней.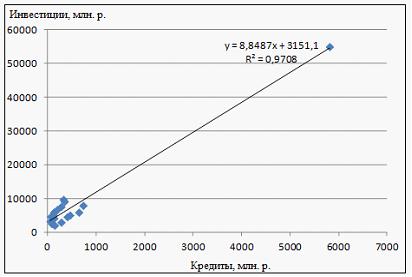


Наличие аномально больших значений способствует высокому значению коэффициента детерминации, поскольку для минимизации суммы квадратов отклонений уравнение регрессии обязательно должно пройти через аномальную точку.

Если исключить аномальное значение и построить поле корреляции и уравнение регрессии, а также рассчитать коэффициент детерминации (см. на рисунке), то можно заметить, что связь между переменными не является сильной и высокой прогнозной силой уравнение не обладает.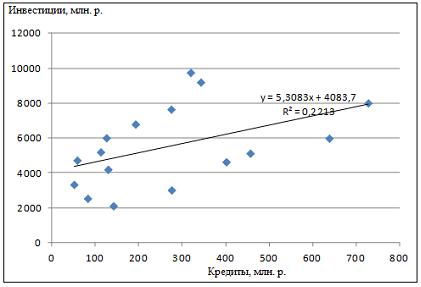