Вопрос Пусть y
 Скачать 0.76 Mb. Скачать 0.76 Mb.
|
|
Кейс 4, задача 3 В таблице представлены данные по субъектам федерации Центрального федерального округа, за исключением Москвы. Области упорядочены по возрастанию независимой переменной х– объему кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам. 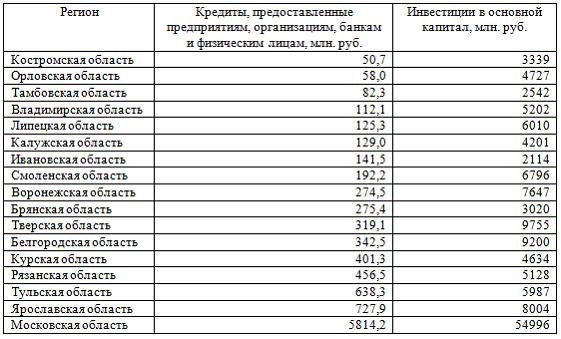 По данной выборке построено уравнение регрессии y = 3151,1 + 8,8487 · x. Коэффициент детерминации R2= 0,9708. Исключив из выборки аномальное значение (Московскую область) и построив уравнение линейной зависимости, можно утверждать, что … между объемом кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам, и инвестициями в основной капитал нет линейной зависимости коэффициент регрессии в полученном уравнении оказался незначимым, значит, его можно признать равным нулю при увеличении объема кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам на 1 млн руб., инвестиции в основной капитал увеличиваются на 5,3 млн руб. при увеличении объема кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам на 1 млн руб., инвестиции в основной капитал уменьшаются на 5,3 млн руб. Решение: Если исключить аномальное значение и построить поле корреляции и уравнение регрессии, а также рассчитать коэффициент детерминации (см. на рисунке), то можно заметить, что связь между переменными является слабой. 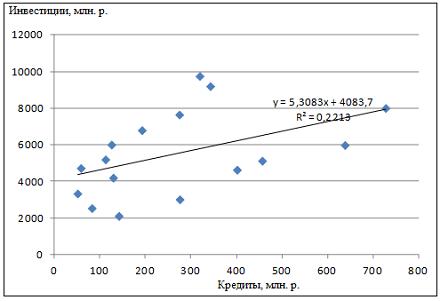 Значит, можно сделать вывод, что между объемом кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам, и инвестициями в основной капитал по Центральному федеральному округу нет линейной зависимости. Кроме того, в уравнении y = 4083,7 + 5,3083 · x коэффициент регрессии b является незначимым и его можно считать равным нулю. Кейс 4, задача 4 В таблице представлены данные по субъектам федерации Центрального федерального округа, за исключением Москвы. Области упорядочены по возрастанию независимой переменной х– объему кредитов, предоставленных предприятиям, организациям, банкам и физическим лицам.  По данной выборке построено уравнение регрессии y = 3151,1 + 8,8487 · x. Коэффициент детерминации R2= 0,9708. В уравнении, параметры которого являются значимыми, коэффициент ____________ показывает, на сколько единиц измерения изменится зависимая переменная у, если независимая переменная x увеличится на 1 единицу измерения. Ответ: регрессии Кейс 5, задача 1 Динамика показателя среднедушевого денежного дохода населения России в период 2005–2011 гг. характеризуется данными, представленными на графике. 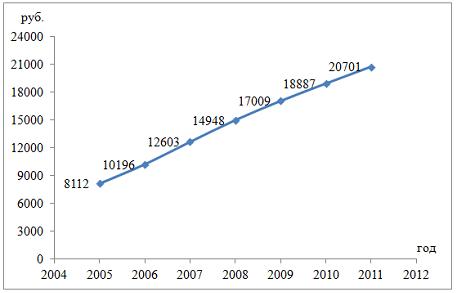 Процесс построения функции тренда для временного ряда называется … аналитическим выравниванием Кейс 5, задача 2 Динамика показателя среднедушевого денежного дохода населения России в период 2005–2011 гг. характеризуется данными, представленными на графике.  Установите соответствие между порядком коэффициента автокорреляции и его значением. 1. Коэффициент автокорреляции первого порядка 2. Коэффициент автокорреляции второго порядка 3. Коэффициент автокорреляции третьего порядка 1. 0,999097 2. 0,998123 3. 0,998261 Кейс 5, задача 3 ПЕРЕПРОВЕРИТЬ! Динамика показателя среднедушевого денежного дохода населения России в период 2005–2011 гг. характеризуется данными, представленными на графике.  Значение среднедушевого денежного дохода населения в 2012 г., рассчитанное на основе линейного тренда, составит _____ руб. (Полученное значение округлите до целых.) Ответ: 23145 Кейс 6, задача 1 Динамика показателя среднемесячной номинальной начисленной заработной платы работников организаций РФ в период 2005–2011 гг. характеризуется данными, представленными на графике. 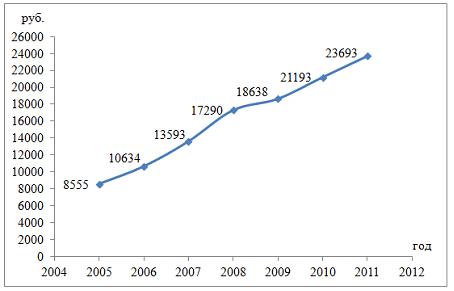 Выявление структуры временного ряда возможно путем анализа значений … автокорреляционной функции Кейс 6, задача 2 Динамика показателя среднемесячной номинальной начисленной заработной платы работников организаций РФ в период 2005–2011 гг. характеризуется данными, представленными на графике.  Установите соответствие между порядком коэффициента автокорреляции и его значением. 1. Коэффициент автокорреляции первого порядка 2. Коэффициент автокорреляции второго порядка 3. Коэффициент автокорреляции третьего порядка 1. 0,98673 2. 0,97640 3. 0,99860 Кейс 6, задача 3 Динамика показателя среднемесячной номинальной начисленной заработной платы работников организаций РФ в период 2005–2011 гг. характеризуется данными, представленными на графике.  Значение среднемесячной номинальной начисленной заработной платы работников организаций РФ в 2012 г., рассчитанное на основе линейного тренда, составит _____ руб. (Полученное значение округлите до целых.) Ответ: 26453 |
