Вопрос1 Статистическая обработка результатов эксперимента

• Название: Вопрос1 Статистическая обработка результатов эксперимента
• Анкор: fizika.doc
• Дата: 16.01.2018
• Размер: 6.64 Mb.
• Имя файла: fizika.doc
• Тип: Документы; #14141
• страница: 6 из 12

ВОПРОС 21

1.Закон Кулона Точечным называется заряд, сосредоточенный на теле, линейные размеры которого пренебрежимо малы по сравнению с расстоянием до других заряженных тел, с которыми он взаимодействует. Понятие точечного заряда, как и материальной точки, является физической абстракциейЗакон Кулона Сила взаимодействия F между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам q1 и q2 и обратно пропорциональна квадрату расстояния r12 между ними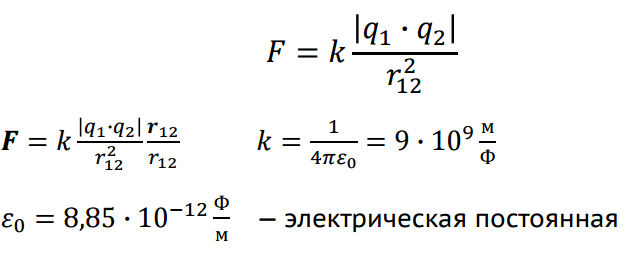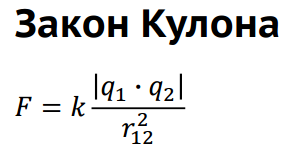



2. Электростатическое поле – поле, которое создается неподвижными электрическими зарядами.

Напряженность поля – силовая характеристика электрического поля.

Напряженность электростатического поля в данной точке есть физическая величина, определяемая силой, действующей на пробный единичный положительный заряд, помещенный в эту точку поля

Потенциал электрического поля - φ

Скалярная физическая величина, введенная для количественного оценивания способности поля перемещать заряженные частицы и равная отношению энергии W ,характеризующей изменение состояния положительно заряженной частицы при ее перемещении из данной точки в бесконечно удаленную, к заряду q этой частицы: φ= W/q. Потенциал является энергетической характеристикой поля. Он численно равен работе, которую надо затратить против сил электрического поля при перенесении единичного положительного точечного заряда из бесконечности в данную точку поля. Единица измерения потенциала - вольт. С учетом

Когда поле образовано несколькими произвольно расположенными зарядами  ,

потенциал его  в данной точке равен алгебраической сумме потенциалов  , создаваемых каждым зарядом в отдельности, т.е.



Потенциальная энергия поля

W = −qEx.

потенциальная энергия заряда в однородном электростатическом поле. Через x обозначена абсцисса точки, в которой ищется потенциальная энергия. Нулевой уровень потенциальной энергии в данном случае соответствует началу координат x = 0 и на рисунках изображён пунктирной линией, перпендикулярной линиям напряжённости

Потенциальная энергия взаимодействия точечных зарядов .Пусть два точечных заряда q1 и q2 находятся в вакууме на расстоянии r друг от друга. Можно показать, что потенциальная энергия их взаимодействия даётся формулой:



ВОПРОС 22

классическая статистика была создана ранее квантовой механики. Поэтому представления классической статистики не учитывают квантовомеханических свойств частиц и особенностей их взаимодействия. Паули, так как допускает, что в любом энергетическом состоянии возможно размещение любого количества частиц. 

Классическая статистика и квантовая статистика различаются исходными принципами в подсчете термодинамической вероятности. 

Классическая статистика помогает физику-экспериментатор у обрабатывать результаты своего эксперимента с минимальной потерей информации. Однако цель эксперимент может состоять и в том, чтобы решить вопрос о правильности какой-либо гипотезы или о правильном значении фундаментальной константы, или просто о том, что делать дальше. В этой главе мы кратко опишем такую теорию. Основной подход теории решений может быть лучше всего проиллюстрирован простым примером. [

Классическая статистика была создана ранее квантовой механики. Поэтому представления классической статистики не учитывают квантовомеханических свойств частиц и особенностей их взаимодействия. Паули, так как допускает, что в любом энергетическом состоянии возможно размещение любого количества частиц

Согласно классической статистике вследствие теплового движения в пучке атомов возможны любые направления, так что можно ожидать уширения пучка в магнитном поле, имеющего непрерывный характер. Однако для пучка атомов серебра наблюдалось расщепление на два луча, соответствующих ориентации под углами О и тс к полю ( отсутствие ориентации под углом тг / 2 имеет особую причину - см. стр. 

Согласно классической статистике повышение температуры может вызывать возрастание энергии любого электрона. Однако по статистике Ферми - Дирака при повышении температуры от абсолютного нуля электроны, занимающие низкий энергетический уровень, не могут перейти сразу на более высокие уровни, так как последние заняты другими электронами. Таким образом, оказывается, что первоначальное повышение температуры влияет только на находящиеся вблизи максимального энергетического уровня WWi электроны, которые могут переходить на высшие незанятые уровни. При дальнейшем увеличении температуры число электронов, переходящих на более высокие уровни, непрерывно возрастает, и при очень высокой температуре в этом процессе будут участвовать все электроны. Однако такая температура для большинства металлов оказывается выше температуры их плавления, поэтому в реальных катодах при рабочих температурах не все электроны будут переходить на высшие уровни. 

Поэтомуклассическая статистика оказалась не в состоянии удовлетворительно объяснять физические явления, наблюдавшиеся в таких коллективах частиц, где квантовомеханические свойства играют важную роль, - например в электронном газе металлов. Квантовая статистика частиц была создана Возе и Энштейном для коллектива частиц с целочисленным спином ( например, фотонов), которые называют бозонами. Применительно к коллективу частиц с полуцеяым спином ( фермионы), подчиняющихся принципу Паули, в том числе и электронов, квантовая статистика разработана Ферми и Дираком. 

Представленияклассической статистики полностью применимы для твердых тел в области высоких и средних температур. При низких температурах необходима квантовая теория. 

Вклассической статистике функция распределения р ( р, q) непосредственно дает распределение вероятностей различных значений координат и импульсов частиц тела

БИЛЕТ 23

Теорема Остроградского-Гаусса для электростатического поля в вакууме.

Фо́рмула Острогра́дского — математическая формула, которая выражает поток векторного поля через замкнутую поверхностьинтегралом от дивергенции этого поля по объёму, ограниченному этой поверхностью:



то есть интеграл от дивергенции векторного поля , распространённый по некоторому объёму , равен потоку вектора через поверхность , ограничивающую данный объём.

Формула применяется для преобразования объёмного интеграла в интеграл по замкнутой поверхности.

В работе Остроградского формула записана в следующем виде: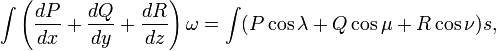



где  и — дифференциалы объёма и поверхности соответственно. В современной записи — элемент объёма, — элемент поверхности. — функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью.

Обобщением формулы Остроградского является формула Стокса для многообразий с краем.

(2) 

Формула (2) выражает теорему Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на ε₀. Эта теорема получена математически для векторного поля произвольной природы русским математиком М.В.Остроградским (1801—1862), а затем независимо от него применительно к электростатическому полю — К. Гауссом. 

В общем случае электрические заряды могут быть распределены с некоторой объемной плотностью ρ=dQ/dV, которая различна в разных местах пространства. Тогда суммарный заряд, заключенный внутри замкнутой поверхности S, которая охватывает некоторый объем V, 

 (3) 

Используя формулу (3), теорему Гаусса (2) можно записать так: 



БИЛЕТ 24

В отличие от проводников, в диэлектриках нет свободных зарядов. Все заряды являются связанными: электроны принадлежат своим атомам, а ионы твёрдых диэлектриков колеблются вблизи узлов кристаллической решётки. Соответственно, при помещении диэлектрика в электрическое поле не возникает направлен- ного движения зарядов1 . Поэтому для диэлектриков не проходят наши доказательства свойств проводников — ведь все эти рассуждения опирались на возможность появления тока. И дей- ствительно, ни одно из четырёх свойств проводников, сформулированных в предыдущей статье, не распростаняется на диэлектрики. 1. Напряжённость электрического поля внутри диэлектрика может быть не равна нулю. 2. Объёмная плотность заряда в диэлектрике может быть отличной от нуля. 3. Линии напряжённости могут быть не перпендикулярны поверхности диэлектрика. 4. Различные точки диэлектрика могут иметь разный потенциал. Стало быть, говорить о «потенциале диэлектрика» не приходится. Диэлектрическая проницаемость Но тем не менее, одно важнейшее общее свойство у диэлектриков имеется, и вам оно известно (вспомните формулу напряжённости поля точечного заряда в диэлектрике!). Напряжённость поля уменьшается внутри диэлектрика в некоторое число ε раз по сравнению с вакуумом. Величина ε даётся в таблицах и называется диэлектрической проницаемостью диэлектрика. Давайте разберёмся, каковы причины ослабления поля в диэлектрике. Рассмотрим диэлек- трик, помещённый во внешнее однородное (для простоты) поле E0. Опыт показывает, что на противоположных поверхностях диэлектрика появляются заряды разных знаков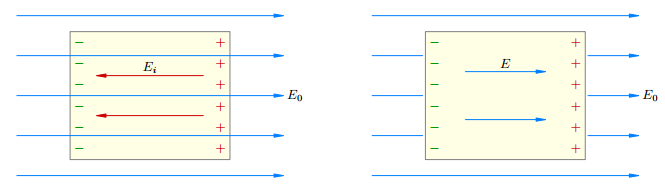



Эти индуцированные заряды расположены так, что создаваемое ими поле Ei внутри ди- электрика направлено против внешнего поля E0 (рис. 1, слева). При этом Ei < E0, так что 1Впрочем, в достаточно сильном электрическом поле может случиться пробой диэлектрика (пример — мол- ния во время грозы). Подобное явление мы изучим позже, при рассмотрении электрического тока в газах. 1внешнее поле ослабляется лишь частично (а не гасится полностью, как внутри проводника). Результирующее поле внутри диэлектрика равно: E = E0 − Ei . Мы видим, что E < E0. Данный факт как раз и подчёркивается следующей формой записи: E = E0 ε . Результирующее поле E направлено в ту же сторону, что и внешнее поле E0 (рис. 1, справа; искажение поля снаружи диэлектрика считаем пренебрежимо малым). Хорошо, но откуда в диэлектрике берутся поверхностные индуцированные заряды? Это — явление поляризации, свойственное всем диэлектрикам. Механизмы поляризации могут быть различными. Мы рассмотрим два типа поляризации: ориентационную и электронную

Диэлектрическая восприимчивость ( поляризуемость ) вещества — физическая величина, мера способности вещества поляризоваться под действием электрического поля. Диэлектрическая восприимчивость  — коэффициент линейной связи между поляризацией диэлектрика P и внешним электрическим полем E в достаточно малых полях:

 ,где  — электрическая постоянная; произведение  называется абсолютной диэлектрической восприимчивостью . В случае вакуума



У диэлектриков, как правило, она положительна. Диэлектрическая восприимчивость измеряется в ничём (безразмерная величина).

Поляризуемость связана с диэлектрической проницаемостью ε соотношением:  , или  .

Вопрос №25

Конденсаторы- устройства, обладающие способностью при малых раз­мерах и небольших относительно окружа­ющих тел потенциалах накапливать зна­чительные по величине заряды, иными сло­вами, обладать большой емкостью.

Конденсатор состоит из двух провод­ников (обкладок), разделенных диэлект­риком. На емкость конденсатора не должны оказывать влияния окружающие тела, поэ­тому проводникам придают такую форму, чтобы поле, создаваемое накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1) две плоские пластины; 2) два коакси­альных цилиндра; 3) две концентрические сферы. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, цилиндрические и сферические.

Электроемкость — скалярная, физическая величина характеризующая способность проводника или системы проводников накапливать электрический заряд. За величину электроемкости система проводников принимают отношение модуля заряда одного из проводников к разности потенциалов между этим проводником и соседним.

С=q/u=c/(₁-₂)

Под емкостью конденсатора по­нимается физическая величина, равная отношению заряда Q, накопленного в кон­денсаторе, к разности потенциалов (₁-₂) между его обкладками.

Вывод формулы емкости плоского конденсатора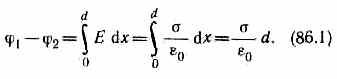



C=Q/(₁-₂)

₁-₂=d/(₀)

Q=S

C=₀S/d

Вопрос №26

В электродинамике — разделе учения об электричестве, в котором рассматривают­ся явления и процессы, обусловленные движением электрических зарядов или макроскопических заряженных тел,—важ­нейшим понятием является понятие элек­трического тока. Электрическим током называется любое упорядоченное (направленное) движение электрических зарядов.

Количественной мерой электрического тока служит сила тока I — скалярная фи­зическая величина, определяемая элек­трическим зарядом, проходящим через по­перечное сечение проводника в единицу времени:

I=dQ/dt.

Ток, сила и направление которого не изме­няются со временем, называется посто­янным. Для постоянного тока

I=Q/t,

где Q — электрический заряд, проходя­щий за время t через поперечное сечение проводника.

Единица силы тока — ампер (А)

Немецкий физик Г. Ом (1787—1854) эк­спериментально установил, что сила то­ка I, текущего по однородному металличе­скому проводнику (т. е. проводнику, в ко­тором не действуют сторонние силы), пропорциональна напряжению Uна кон-цах проводника:I=U/R, (98.1)

где R— электрическое сопротивление про­водника. Уравнение (98.1) выражает за­кон Ома для участка цепи (не содержаще­го источника э.д.с.): сила тока в проводни­ке прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.

Закон Ома можно представить в диф­ференциальной форме.

I/S=(1/)(U/l) (98.3)

где величина обратная удельному сопротивлению, на­зывается удельной электрической прово­димостью вещества проводника. Ее едини­ца— сименс на метр (См/м). Учитывая, что U/l=E—напряженность электриче­ского поля в проводнике, I/S = j— плот­ность тока, формулу можно запи­сать в виде

j=E. (98.4)

Так как в изотропном проводнике носите­ли тока в каждой точке движутся в на­правлении вектора Е, то направления j и Е совпадают. Поэтому формулу можно записать в виде

j=E. (98.5)

Выражение (98.5) — закон Ома в диффе­ренциальной форме, связывающий плот­ность тока в любой точке внутри провод­ника с напряженностью электрического поля в этой же точке. Это соотношение справедливо и для переменных полей.

Теперь рассмот­рим неоднородный участок цепи, где дей­ствующую э.д.с. на участке 1—2 обозна­чим через ξ₁₂, а приложенную на концах участка разность потенциалов — через

₁-₂.

Если ток проходит по неподвижным проводникам, образующим участок 1—2, то работа A₁₂всех сил (сторонних и элек­тростатических), совершаемая над носите­лями тока, по закону сохранения и пре­вращения энергии равна теплоте, выделя­ющейся на участке. Работа сил, со­вершаемая при перемещении заряда Q₀ на участке 1—2,

A₁₂=Q₀ξ12 + Q₀(₁-₂).

Э.д.с. ξ₁₂, как и сила тока I,— величи­на скалярная. Ее необходимо брать либо с положительным, либо с отрицательным знаком в зависимости от знака работы, совершаемой сторонними силами. Если

э.д.с. способствует движению положитель­ных зарядов в выбранном направлении (в направлении 1—2), то ξ₁₂>0. Если э.д.с. препятствует движению положитель­ных зарядов в данном направлении, то

ξ₁₂<0.

За время tв проводнике выделяется теплот

Q=I²Rt=IR(It)=IRQ₀.



Выражение (100.3) или (100.4) представ­ляет собой закон Ома для неоднородного участка цепи в интегральной форме, кото­рый является обобщенным законом Ома.

Вопрос 27

Обобщенный закон Ома по­зволяет рассчитать практически любую сложную цепь. Однако непосредственный расчет разветвленных цепей, содержащих несколько замкнутых контуров (контуры могут иметь общие участки, каждый из контуров может иметь несколько источни­ков э.д.с. и т. д.), довольно сложен. Эта задача решается более просто с помощью двух правил Кирхгофа.

Любая точка разветвления цепи, в ко­торой сходится не менее трех проводников с током, называется узлом. При этом ток, входящий в узел, считается положитель­ным, а ток, выходящий из узла,— отрица­тельным.