Вопрос1 Статистическая обработка результатов эксперимента
 Скачать 6.64 Mb. Скачать 6.64 Mb.
|
Основные кинематические величины.Перемещение — векторная физическая величина, равная разности радиус-векторов в конечный и начальный моменты времени: Иными словами, перемещение — это приращение радиус-вектора за выбранный промежуток времени. Средняя скорость — векторная физическая величина равная отношению вектора перемещения к промежутку времени, за который происходит это перемещение: Скорость — векторная физическая величина, равная первой производной от радиус-вектора по времени: Характеризует быстроту перемещения материальной точки. Единица измерения скорости в системе СИ— м/с, в системе СГС — см/с. Мгновенная скорость всегда направлена по касательной к траектории. Ускорение — векторная физическая величина, равная второй производной от радиус-вектора по времени и, соответственно, первой производной от мгновенной скорости по времени: Характеризует быстроту изменения скорости. Единица ускорения в системе СИ— м/с², в системе СГС — см/с². В случае движения в плоскости вектор ускорения можно разложить по сопутствующему базису: на вектор нормального и тангенциального ускорения: Здесь — единичный вектор нормали, — единичный вектор касательной. Величина называется нормальным ускорением и характеризует скорость изменения направления движения. Нормальное ускорение выражается через мгновенную скорость и радиус кривизны траектории: В случае движения по окружности нормальное ускорение называется центростремительным. Как видно из предыдущей формулы, при движении по окружности с постоянной скоростью нормальное ускорение постоянно по модулю и направлено к центру окружности. Величина называется тангенциальным ускорением и характеризует величину изменения модуля скорости: Вопрос №3)Законы динамики материальной точки. Дина́мика — раздел механики, в котором изучаются причины возникновения механического движения. Для динамики характерны такие понятия, как масса, сила, импульс, момент импульса, энергия. Все задачи в динамике делятся на прямую и обратную задачи..
Классическая динамика основана на трёх основных законах Ньютона: I закон Ньютона: Существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или их действие скомпенсировано. II закон Ньютона: В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки. 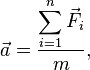 где — ускорение тела, — силы, приложенные к материальной точке, а — её масса. Также второй закон можно записать в виде: В классической (ньютоновской) механике масса материальной точки полагается постоянной во времени и независящей от каких-либо особенностей её движения и взаимодействия с другими телами. Второй закона Ньютона можно также сформулировать с использованием понятия импульса: скорость изменения импульса материальной точки равна действующей на точку силе где — импульс (количество движения) точки, — её скорость, а — время. При такой формулировке, как и ранее, полагают, что масса материальной точки неизменна во времени. III закон Ньютона: Силы, с которыми тела действуют друг на друга, лежат на одной прямой, имеют противоположные направления и равные модули Если при этом рассматриваются взаимодействующие материальные точки, то обе эти силы действуют вдоль прямой, их соединяющей. Это приводит к тому, что суммарный момент импульса системы состоящей из двух материальных точек в процессе взаимодействия остается неизменным. Таким образом, из второго и третьего законов Ньютона могут быть получены законы сохранения импульса и момента импульса В динамике существует инерциальная и неинерциальная система отсчета. Инерциа́льная систе́ма отсчёта (ИСО) — система отсчёта, в которой все свободные тела движутся прямолинейно и равномерно или покоятся. Иногда также говорят что: «Инерциальной называется система отсчёта, по отношению к которой пространство является однородным и изотропным, а время — однородным». Законы Ньютона, а также все остальные аксиомы динамики в классической механике формулируются по отношению к инерциальным системам отсчёта. Неинерциа́льная систе́ма отсчёта — система отсчёта, в которой не выполняется первый закон Ньютона — «закон инерции», говорящий о том, что каждое тело, в отсутствие действующих на него сил, покоится либо движется по прямой и с постоянной скоростью. Всякая система отсчета, движущаяся с ускорением или поворачивающаяся относительно инерциальной, является неинерциальной. Второй закон Ньютона также не выполняется в неинерциальных системах отсчёта. Для того чтобы уравнение движения материальной точки в неинерциальной системе отсчёта по форме совпадало с уравнением второго закона Ньютона, дополнительно к «обычным» силам, действующим в инерциальных системах, вводят силы инерции. Законы Ньютона выполняются только в инерциальных системах отсчёта. Для того, чтобы найти уравнение движения в неинерциальной системе отсчёта, нужно знать законы преобразования сил и ускорений при переходе от инерциальной системы к любой неинерциальной. Вопрос№4) Импульс материальной точки. И́мпульс (Коли́чество движе́ния) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости: По II закону Ньютона скорость изменения импульса материальной точки равна действующей на точку силе Это формула носит название закона изменения импульса материальной точки. Для системы материальных точек вышеуказанная формула принимает вид: 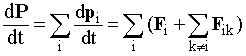 Закон изменения импульса для системы,где Fik - внутренние силы взаимодействия i-й и k-й частиц системы между собой; Fi - равнодействующая внешних сил, приложенных к i-й частице. Свойства импульса.
Зако́н сохране́ния и́мпульса(Зако́н сохране́ния количества движения) – импульс замкнутой системы тел не меняется с течением времени. Σp = const т.е. m1v1+m2v2=m1'v1'+m2'v2' Замкнутая система сил- система на которую не действуют внешние силы. Закон сохранения импульса является следствием из второго и третьего законов Ньютона. Закон сохранения импульса выполняется не только для систем, на которые не действуют внешние силы, но и для систем, сумма всех внешних сил которых равна нулю. Равенство нулю всех внешних сил достаточно, но не необходимо для выполнения закона сохранения импульса. Вопрос№5)Механическая работа. Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек), тела или системы. Обычно обозначается символом A. При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения:  Здесь точкой обозначено скалярное произведение, — вектор перемещения; подразумевается, что действующая сила постоянна в течение всего того времени, за которое вычисляется работа. В общем случае, когда сила не постоянна, а движение не прямолинейно, работа вычисляется как криволинейный интеграл второго рода по траектории точки: Если существует зависимость силы от координат, интеграл определяется следующим образом: 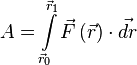 , ,где и — радиус-векторы начального и конечного положения тела соответственно.
|
