Вопрос1 Статистическая обработка результатов эксперимента
 Скачать 6.64 Mb. Скачать 6.64 Mb.
|
|
Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю: Первое правило Кирхгофа вытекает из закона сохранения электрического заряда. Второе правило Кирхгофа получается из обобщенного закона Ома для разветвленных цепей. Выбор направления обхода совершенно произволен. Все токи, совпадающие по направлению с направлением обхода контура, считаются положительными, не совпадающие с направлением обхода — отрицательными. Источники э.д.с. считаются положительными, если они создают ток, направленный в сторону обхода контура. Второе правило Кирхгофа: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов Ii, на сопротивления Ri соответствующих участков этого контура равна алгебраической сумме э.д.с. ξ k, встречающихся в этом контуре. При расчете сложных цепей постоянного тока с применением правил Кирхгофа необходимо: 1. Выбрать произвольное направление токов на всех участках цепи; действительное направление токов определяется при решении задачи: если искомый ток получится положительным, то его направление было выбрано правильно, отрицательным — его истинное направление противоположно выбранному. 2. Выбрать направление обхода контура и строго его придерживаться; произведение IRположительно, если ток на данном участке совпадает с направлением обхода, и наоборот, э.д.с., действующие по выбранному направлению обхода, считаются положительными, против — отрицательными. 3. Составить столько уравнений, чтобы их число было равно числу искомых величин (в систему уравнений должны входить все сопротивления и э.д.с. рассматриваемой цепи); каждый рассматриваемый контур должен содержать хотя бы один элемент, не содержащийся в предыдущих контурах, иначе получатся уравнения, являющиеся простой комбинацией уже составленных. Вопрос №28 Магнитное поле оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы. Обобщая результаты исследования действия магнитного поля на различные проводники с током, Ампер установил, что сила dF, с которой магнитное поле действует на элемент проводника dl с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длиной dl проводника на магнитную индукцию В: dF = I[dl, В]. Направление вектора dF может быть найдено, согласно, по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток. Модуль силы Ампера вычисляется по формуле dF = IBdlsin, где — угол между векторами dl и В. Вопрос №29 Закон Био — Савара — Лапласа для проводника с током I, элемент которого dlсоздает в некоторой точке А (рис. 164) индукцию поля dB, записывается в виде  где dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r — радиус-вектор, 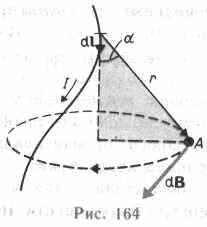 проведенный из элемента dl проводника в точку А поля, r— модуль радиуса-вектора г. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление dB, если поступательное движение винта соответствует направлению тока в элементе. Модуль вектора dB определяется выражением 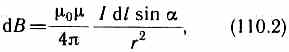 где а — угол между векторами dl и г. Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности: 1. Магнитное поле прямого тока — тока, текущего по тонкому прямому про- 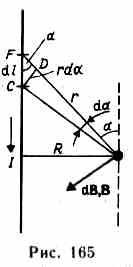 воду бесконечной длины (рис. 165). В произвольной точке А, удаленной от оси проводника на расстояние R, векторы dB от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов dB можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол а (угол между векторами dl и r), выразив через него все остальные величины. Из рис. 165 следует, что 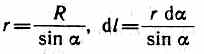 (радиус дуги CDвследствие малости dlравен r, и угол FDCпо этой же причине можно считать прямым). Подставив эти выражения в (110.2), получим, что магнитная индукция, создаваемая одним элементом проводника, равна 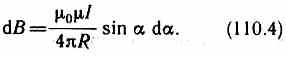 Так как угол а для всех элементов прямого тока изменяется в пределах от 0 до я, то, согласно (110.3) и (110.4), 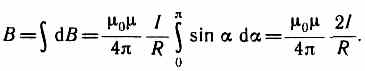 Следовательно, магнитная индукция поля прямого тока 2. Магнитное поле в центре кругового проводника с током (рис. 166). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитное поле одинакового направления — вдоль нормали от витка. 180  Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sin=1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2),  Тогда 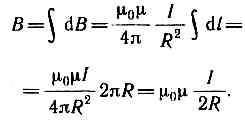 Следовательно, магнитная индукция поля в центре кругового проводника с током 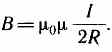  Вопрос 34 Электромагнитная индукция. Самоиндукция. Вопрос 34 Электромагнитная индукция. Самоиндукция.Электромагнитная индукция. Электрические токи создают вокруг себя магнитное поле. 1831 г. английский физик М. Фарадей открыл явление электромагнитной индукции (заключающееся в том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает электрический ток, получивший название индукционного). Опытным путем было также установлено, что значение индукционного тока совершенно не зависит от способа изменения потока магнитной индукции, а определяется лишь скоростью его изменения. Открытие явления электромагнитной индукции имело большое значение, так как была доказана возможность получения электрического тока с помощью магнитного поля. Закон Фарадея и его вывод из закона сохранения энергии: Фарадей пришел к количественному закону электромагнитной индукции. Он показал, что всякий раз, когда происходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электромагнитной индукции. Значение индукционного тока, а следовательно, и э. д. с, электромагнитной индукции ξiопределяются только скоростью изменения магнитного потока, т. е.  закона электромагнитной индукции Фарадея: какова бы ни была причина изменения потока магнитной индукции, охватываемого замкнутым проводящим контуром, возникающая в контуре э.д.с. 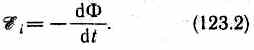 Знак минус показывает, что увеличение потока (dФ/dt>0) вызывает э.д.с. ξξi<0, т. е. поле индукционного тока направлено навстречу потоку; уменьшение потока (dФ/dt<0 ) вызывает ξi>0, т. е. направления потока и поля индукционного тока совпадают. Знак минус в формуле (123.2) является математическим выражением правила Ленца — общего правила для нахождения направления индукционного тока, выведенного в 1833 г. Правило Ленца: индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток. Закон Фарадея э.д.с. ξi электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром. Этот закон является универсальным: э.д.с. ξiне зависит от способа изменения магнитного потока. Э.д.с. электромагнитной индукции выражается в вольтах. Действительно, учитывая, что единицей магнитного потока является вебер (Вб), получим  При вращении рамки в ней будет возникать переменная э.д.с. индукции (см. (123.2))  Вихревые токи (токи Фуко) Индукционный ток возникает не только в линейных проводниках, но и в массивных сплошных проводниках, помещенных в переменное магнитное поле. Эти токи оказываются замкнутыми в толще проводника и поэтому называются вихревыми. Их также называют токами Фуко — по имени первого исследователя. Токи Фуко, как и индукционные токи в линейных проводниках, подчиняются правилу Ленца: их магнитное поле направлено так, чтобы противодействовать изменению магнитного потока, индуцирующего вихревые токи. Индуктивность контура. Самоиндукция Электрический ток, текущий в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого, по закону Био — Савара—Лапласа (см. (110.2)), пропорциональна току. Сцепленный с контуром магнитный поток Ф поэтому пропорционален току I в контуре: Ф=LI, (126.1) где коэффициент пропорциональности Lназывается индуктивностью контура. При изменении силы тока в контуре будет изменяться также и сцепленный с ним магнитный поток; следовательно, в контуре будет индуцироваться э.д.с. Возникновение э.д.с. индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией. Из выражения (126.1) определяется единица индуктивности генри (Гн): 1 Гн — индуктивность такого контура, магнитный поток самоиндукции которого при токе в 1 А равен 1 Вб: 1 Гн=1 Вб/А=1В•с/А. 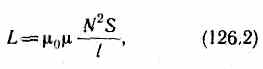 т. е. индуктивность соленоида зависит от числа витков соленоида N, его длины l, площади S и магнитной проницаемости вещества, из которого изготовлен сердечник соленоида. Применяя к явлению самоиндукции закон Фарадея (см. (123.2)), получим, что э.д.с. самоиндукции 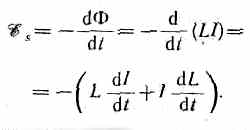 Если контур не деформируется и магнитная проницаемость среды не изменяется (в дальнейшем будет показано, что последнее условие выполняется не всегда), то L=const и 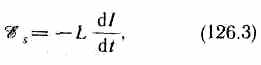 Вопрос №30 Действие магнитного поля на движущийся заряд Опыт показывает, что магнитное поле действует не только на проводники с током (см. §111), но и на отдельные заряды, движущиеся в магнитном поле. Сила, действующая на электрический заряд Q, движущийся в магнитном поле со скоростью v, называется силой Лоренца и выражается формулой F=Q[vB], (114.1) где В — индукция магнитного поля, в котором заряд движется. Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для Q> 0 направления I и v совпадают, для Q<0—противоположны), то отогнутый большой палец покажет направление силы, действующей на положительный заряд. На рис. 169 показана взаимная ориентация векторов v, В (поле направлено к нам, на рисунке показано точками) и F для положительного заряда. На отрицательный заряд сила действует в противоположном направлении.  Модуль силы Лоренца (см. (114.1)) равен F=QvBsin, где — угол между v и В. Отметим еще раз (см. § 109), что магнитное поле не действует на покоящийся электрический заряд. В этом существенное отличие магнитного поля от электрического. Магнитное поле действует только на движущиеся в нем заряды. Так как по действию силы Лоренца можно определить модуль и направление вектора В, то выражение для силы Лоренца может быть использовано (наравне с другими, см. § 109) для определения вектора магнитной индукции В. Сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, поэтому она изменяет только направление этой скорости, не изменяя ее модуля. Следовательно, сила Лоренца работы не совершает. Иными словами, постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изменяется. Если на движущийся электрический заряд помимо магнитного поля с индукцией В действует и электрическое поле с напряженностью Е, то результирующая сила F, приложенная к заряду, равна векторной сумме сил — силы, действующей со стороны электрического поля, и силы Лоренца: F=QE + Q[vB]. Это выражение называется формулой Лоренца. Скорость v в этой формуле есть скорость заряда относительно магнитного поля. Движение заряженных частиц в магнитном поле Выражение для силы Лоренца (114.1) позволяет найти ряд закономерностей движения заряженных частиц в магнитном поле. Направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле зависят от знака заряда Q частицы. На этом основано определение знака заряда частиц, движущихся в магнитных полях. Для вывода общих закономерностей будем считать, что магнитное поле однородно и на частицы электрические поля не действуют. Если заряженная частица движется в магнитном поле со скоростью v вдоль линий магнитной индукции, то угол а между векторами v и В равен 0 или . Тогда по формуле (114.1) сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она движется равномерно и прямолинейно. Если заряженная частица движется в магнитном поле со скоростью v, перпендикулярной вектору В, то сила Лоренца F=Q[vB] постоянна по модулю и нормальна к траектории частицы. Согласно второму закону Ньютона, эта сила создает центростремительное ускорение. Отсюда следует, что частица будет двигаться по окружности, радиус rкоторой определяется из условия QvB = mv2/r, откуда Период вращения частицы, т. е. время Т, затрачиваемое ею на один полный оборот, T = 2nr/v. Подставив сюда выражение (115.1), получим  т. е. период вращения частицы в однородном магнитном поле определяется только величиной, обратной удельному заряду  (Q/m) частицы, и магнитной индукцией поля, но не зависит от ее скорости (при v<< с)). На этом основано действие циклических ускорителей заряженных частиц (см. §116). Если скорость v заряженной частицы направлена под углом а к вектору В (рис. 170), то ее движение можно представить в виде суперпозиции: 1) равномерного прямолинейного движения вдоль поля со скоростью v||=vcos; 2) равномерного движения со скоростью v┴= vsin по окружности в плоскости, перпендикулярной полю. Радиус окружности определяется формулой (115.1) (в данном случае надо заменить vна v┴=vsin). В результате сложения обоих движений возникает движение по спирали, ось которой параллельна магнитному полю (рис. 170). Шаг винтовой линии h=v||T=vTcos. Подставив в последнее выражение (115.2), получим h=2mvcos/(BQ). Направление, в котором закручивается спираль, зависит от знака заряда частицы. Если скорость v заряженной частицы составляет угол а с направлением вектора В неоднородного магнитного поля, индукция которого возрастает в направлении движения частицы, то rи hуменьшаются с ростом В. На этом основана фокусировка заряженных частиц в магнитном поле. Вопрос №31 |
