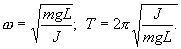Вопрос1 Статистическая обработка результатов эксперимента

• Название: Вопрос1 Статистическая обработка результатов эксперимента
• Анкор: fizika.doc
• Дата: 16.01.2018
• Размер: 6.64 Mb.
• Имя файла: fizika.doc
• Тип: Документы; #14141
• страница: 8 из 12

Ускорителями заряженных частиц назы­ваются устройства, в которых под дей­ствием электрических и магнитных полей создаются и управляются пучки высокоэнергетичных заряженных частиц (элек­тронов, протонов, мезонов и т.д.).

Любой ускоритель характеризуется типом ускоряемых частиц, энергией, со­общаемой частицам, разбросом частиц по энергиям и интенсивностью пучка. Ускорители делятся на непрерывные (из них выходит равномерный по времени пу­чок) и импульсные (из них частицы вы­летают порциями — импульсами). По­следние характеризуются длительностью импульса. По форме траектории и меха­низму ускорения частиц ускорители делят­ся на линейные, циклические и индукци­онные. В линейных ускорителях траекто­рии движения частиц близки к прямым линиям, в циклических и индукционных — траекториями частиц являются окружно­сти или спирали.

Рассмотрим некоторые типы ускорите­лей заряженных частиц.

Циклотрон — циклический резонан­сный ускоритель тяжелых частиц (прото­нов, ионов). Его принципиальная схема приведена на рис. 171. Между полюсами

Фазотрон (синхроциклотрон) — циклический резонансный ускоритель тя­желых заряженных частиц (например, протонов, ионов, -частиц), в котором уп­равляющее магнитное поле постоянно, а частота ускоряющего электрического по­ля медленно изменяется с периодом. Дви­жение частиц в фазотроне, как и в цикло­троне, происходит по раскручивающейся спирали. Частицы в фазотроне ускоряются до энергий, примерно равных 1 ГэВ (огра­ничения здесь определяются размерами фазотрона, так как с ростом скорости частиц растет радиус их орбиты).

Синхрофазотрон — циклический ре­зонансный ускоритель тяжелых заряжен­ных частиц (протонов, ионов), в котором объединяются свойства фазотрона и син­хротрона, т. е. управляющее магнитное поле и частота ускоряющего электрическо­го поля одновременно изменяются во вре­мени так, чтобы радиус равновесной орби­ты частиц оставался постоянным. Протоны ускоряются в синхрофазотроне до энергий 500 ГэВ.

Вопрос №32

Работа по перемещению проводника и контура с током в магнитном поле

На проводник с током в магнитном поле действуют силы, определяемые законом Ампера (см. §111). Если проводник не закреплен (например, одна из сторон кон­тура изготовлена в виде подвижной пере­мычки, рис. 177), то под действием силы Ампера он будет в магнитном поле переме­щаться. Следовательно, магнитное поле совершает работу по перемещению про­водника с током.

Для определения этой работы рас-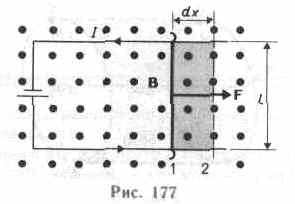



смотрим проводник длиной l с током I (он может свободно перемещаться), помещен­ный в однородное внешнее магнитное по­ле, перпендикулярное плоскости контура. При указанных на рис. 177 направлениях тока и поля сила, направление которой определяется по правилу левой руки, а значение — по закону Ампера (см. (111.2)), равна

F=IBl.

Под действием этой силы проводник пере­местится параллельно самому себе на от­резок Ах из положения 1 в положение 2. Работа, совершаемая магнитным полем, равна

dA=Fdx=IBldx =IBdS= IdФ,

так как ldx=dS— площадь, пересекае­мая проводником при его перемещении в магнитном поле, ВdS=dФ — поток век­тора магнитной индукции, пронизываю­щий эту площадь. Таким образом,

dA=IdФ, (121.1)

т. е. работа по перемещению проводника с током в магнитном поле равна произве­дению силы тока на магнитный поток, пересеченный движущимся проводником. Полученная формула справедлива и для произвольного направления вектора В.

Вычислим работу по перемещению за­мкнутого контура с постоянным током I в магнитном поле. Предположим, что кон­тур М перемещается в плоскости чертежа и в результате бесконечно малого переме­щения займет положение М', изображен­ное на рис. 178 штриховой линией. На­правление тока в контуре (по часовой стрелке) и магнитного поля (перпендику­лярно плоскости чертежа — за чертеж) указано на рисунке. Контур М мысленно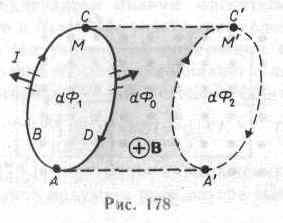



разобьем на два соединенных своими кон­цами проводника: ABCи CDA.

Работа dA, совершаемая силами Ам­пера при рассматриваемом перемещении контура в магнитном поле, равна алгебра­ической сумме работ по перемещению проводников ЛВС (dA₁) и СDA (dА₂), т. е.

dA=dA₁+dA₂. (121.2)

Силы, приложенные к участку CDAконтура, образуют с направлением пере­мещения острые углы, поэтому совершае­мая ими работа dA₂>0. Согласно (121.1), эта работа равна произведению силы то­ка I в контуре на пересеченный проводни­ком CDAмагнитный поток. Провод­ник CDAпересекает при своем движении поток dФ₀ сквозь поверхность, выполнен­ную в цвете, и поток dФ₂, пронизывающий контур в его конечном положении. Сле­довательно,

dA₂= I(dФ₀+dФ₂). (121.3)

Силы, действующие на участок ЛВС контура, образуют с направлением пе­ремещения тупые углы, поэтому совер­шаемая ими работа dA₁<0. Провод­ник ЛВС пересекает при своем движении поток dФ₀ сквозь поверхность, выполнен­ную в цвете, и поток dФ₁, пронизывающий контур в начальном положении. Следова­тельно,

dA₁=I(dФ₀+dФ₁). (121.4)

Подставляя (121.3) и (121.4) в (121.2), получим выражение для эле­ментарной работы:

dA=I(dФ₂ -dФ₁),

где dФ₂-dФ₁=dФ'— изменение магнит­ного потока через площадь, ограниченную контуром с током. Таким образом,

dA=IdФ'. (121.5)

Проинтегрировав выражение (121.5), оп­ределим работу, совершаемую силами Ам­пера, при конечном произвольном переме­щении контура в магнитном поле:

A=IФ, (121.6)

т. е. работа по перемещению замкнутого

контура с током в магнитном поле равна произведению силы тока в контуре на из­менение магнитного потока, сцепленного

с контуром. Формула (121.6) остается справедливой для контура любой формы в произвольном магнитном поле.

Вопрос№33

Всякое вещество является магнетиком, т. е. оно способно под действием магнитно­го поля приобретать магнитный момент (намагничиваться). Для понимания меха­низма этого явления необходимо рассмот­реть действие магнитного поля на движу­щиеся в атоме электроны.

Ради простоты предположим, что элек­трон в атоме движется по круговой орби­те. Если орбита электрона ориентирована относительно вектора В произвольным об­разом, составляя с ним угол а (рис. 188), то можно доказать, что она приходит в та­кое движение вокруг В, при котором век­тор магнитного момента р_m, сохраняя по­стоянным угол а, вращается вокруг на-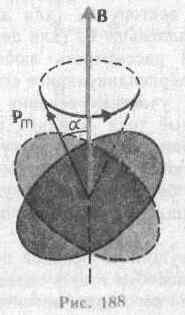



правления В с некоторой угловой скоро­стью. Такое движение в механике на­зывается прецессией. Прецессию вокруг вертикальной оси, проходящей через точку опоры, совершает, например, диск волчка при замедлении движения.

Таким образом, электронные орбиты атома под действием внешнего магнитного поля совершают прецессионное движе­ние, которое эквивалентно круговому то­ку. Так как этот микроток индуцирован внешним магнитным полем, то, согласно правилу Ленца, у атома появляется со­ставляющая магнитного поля, направлен­ная противоположно внешнему полю. На­веденные составляющие магнитных полей атомов (молекул) складываются и обра­зуют собственное магнитное поле вещест­ва, ослабляющее внешнее магнитное по­ле. Этот эффект получил название диа­магнитного эффекта, а вещества, на­магничивающиеся во внешнем магнитном поле против направления поля, называют­ся диамагнетиками.

В отсутствие внешнего магнитного по­ля диамагнетик немагнитен, поскольку в данном случае магнитные моменты элек­тронов взаимно компенсируются, и сум­марный магнитный момент атома (он ра­вен векторной сумме магнитных моментов (орбитальных и спиновых) составляющих атом электронов) равен нулю. К диамагнетикам относятся многие металлы (на­пример, Bi, Ag, Au, Cu), большинство органических соединений, смолы, углерод и т. д.

Так как диамагнитный эффект обус­ловлен действием внешнего магнитного поля на электроны атомов вещества, то диамагнетизм свойствен всем веществам. Однако наряду с диамагнитными ве­ществами существуют и парамагнитные — вещества, намагничивающиеся во внеш­нем магнитном поле по направлению поля.

У парамагнитных веществ при отсутст­вии внешнего магнитного поля магнитные моменты электронов не компенсируют друг друга, и атомы (молекулы) парамагнети­ков всегда обладают магнитным момен­том. Однако вследствие теплового движе­ния молекул их магнитные моменты ори­ентированы беспорядочно, поэтому пара-

магнитные вещества магнитными свой­ствами не обладают. При внесении пара­магнетика во внешнее магнитное поле устанавливается преимущественная ори­ентация магнитных моментов атомов по полю (полной ориентации препятствует тепловое движение атомов). Таким обра­зом, парамагнетик намагничивается, со­здавая собственное магнитное поле, со­впадающее по направлению с внешним полем и усиливающее его. Этот эффект называется парамагнитным. При ослабле­нии внешнего магнитного поля до нуля ориентация магнитных моментов вследст­вие теплового движения нарушается и па­рамагнетик размагничивается. К парамаг­нетикам относятся редкоземельные эле­менты, Pt, Al и т. д. Диамагнитный эффект наблюдается и в парамагнетиках, но он значительно слабее парамагнитного и по­этому остается незаметным.

Из рассмотрения явления парамагне­тизма следует, что его объяснение совпа­дает с объяснением ориентационной (дипольной) поляризации диэлектриков с по­лярными молекулами (см. §87), только электрический момент атомов в случае поляризации надо заменить магнитным моментом атомов в случае намагничения.

Подводя итог качественному рассмот­рению диа- и парамагнетизма, еще раз отметим, что атомы всех веществ являют­ся носителями диамагнитных свойств. Ес­ли магнитный момент атомов велик, то парамагнитные свойства преобладают над диамагнитными и вещество является па­рамагнетиком; если магнитный момент атомов мал, то преобладают диамагнит­ные свойства и вещество является диамагнетиком.

Подобно тому, как для количественного описания поляризации диэлектриков вво­дилась поляризованность (см. §88), для количественного описания намагничения магнетиков вводят векторную величину — намагниченность, определяемую магнит­ным моментом единицы объема магнетика:

J=p_m/V=p_a/V,

где p_m=р_а— магнитный

Согласно представлениям Вейсса, ферромагнетики при температурах ниже точки Кюри обладают спонтанной намаг­ниченностью независимо от наличия внеш­него намагничивающего поля. Спонтанное намагничение, однако, находится в кажу­щемся противоречии с тем, что многие ферромагнитные материалы даже при тем­пературах ниже точки Кюри не намагниче­ны. Для устранения этого противоречия Вейсс ввел гипотезу, согласно которой ферромагнетик ниже точки Кюри разбива­ется на большое число малых макроскопи­ческих областей — доменов, самопроиз­вольно намагниченных до насыщения.

При отсутствии внешнего магнитного поля магнитные моменты отдельных до­менов ориентированы хаотически и ком­пенсируют друг друга, поэтому результи­рующий магнитный момент ферромагнети­ка равен нулю и ферромагнетик не намагничен. Внешнее магнитное поле ори­ентирует по полю магнитные моменты не отдельных атомов, как это имеет место в случае парамагнетиков, а целых об­ластей спонтанной намагниченности. По­этому с ростом Н намагниченность

J (см. рис. 192) и магнитная индукции В (см. рис. 193) уже в довольно слабых полях растут очень быстро. Этим объясня­ется также увеличение ферромагнетиков до максимального значения в слабых по­лях (см. рис. 194). Эксперименты показа­ли, что зависимость В от Я не является такой плавной, как показано на рис. 193, а имеет ступенчатый вид. Это свидетель­ствует о том, что внутри ферромагнетика домены поворачиваются по полю скачком.

При ослаблении внешнего магнитного поля до нуля ферромагнетики сохраняют остаточное намагничение, так как тепло­вое движение не в состоянии быстро дезо­риентировать магнитные моменты столь крупных образований, какими являются домены. Поэтому и наблюдается явление магнитного гистерезиса (рис.195). Для того чтобы ферромагнетик размагнитить, необходимо приложить коэрцитивную си­лу; размагничиванию способствуют также встряхивание и нагревание ферромагнети­ка. Точка Кюри оказывается той темпера­турой, выше которой происходит разруше­ние доменной структуры.

Вопрос 35 Гармонические колебания. Дифференциальное уравнение гармонических колебаний. Пружинный, математический и физический маятники.

Периодические колебания называются гармоническими, если колеблющаяся величина меняется с течением времени по закону косинуса или синуса:



.

Здесь - циклическая частота колебаний, A – максимальное отклонение колеблющейся величины от положения равновесия (амплитуда колебаний), φ(t) = ωt+φ₀ – фаза колебаний, φ₀ – начальная фаза.

График гармонических колебаний представлен на рисунке 1.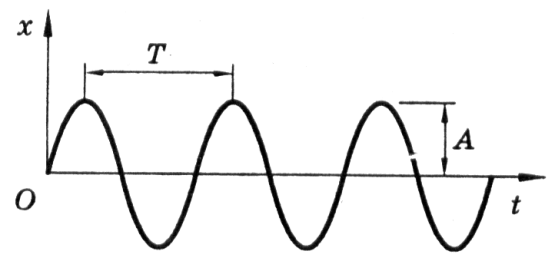



Рисунок 1 – График гармонических колебаний

При гармонических колебаниях полная энергия системы с течением времени не изменяется. Можно показать, что полная энергия механической колебательной системы при гармонических колебаниях равна:

.

Гармонически колеблющаяся величина s(t) подчиняется дифференциальному уравнению:

, (1)

которое называется дифференциальным уравнением гармонических колебаний.

Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести.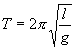



- период кодебаний

Физический маятник.

Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной.



При небольших углах отклонения α (рис. 7.4) физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F.

Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения

 . Момент силы: определить в явном виде нельзя. С учетом всех величин, входящих в исходное дифференциальное уравнение колебаний физического маятника имеет вид:

(7.10)

(7.11)

Решение этого уравнения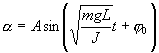


Определим длину l математического маятника, при которой период его колебаний равен периоду колебаний физического маятника, т.е.  или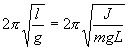

.
Из этого соотношения определяем


Данная формула определяет приведенную длину физического маятника, т.е. длину такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.

Пружинный маятник

Это груз, прикрепленный к пружине, массой которой можно пренебречь.

Пока пружина не деформирована, сила упругости на тело не действует. В пружинном маятнике колебания совершаются под действием силы упругости.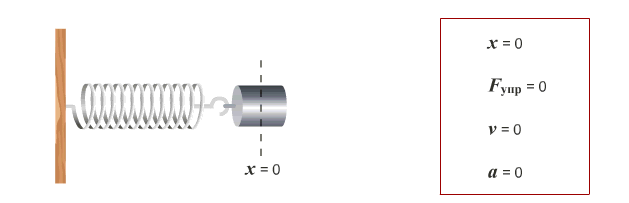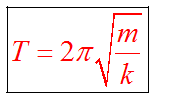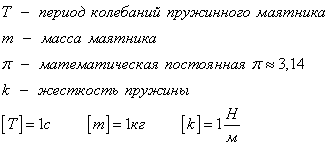




Вопрос 36 Энергия гармонических колебаний

При гармонических колебаниях полная энергия системы с течением времени не изменяется. Можно показать, что полная энергия механической колебательной системы при гармонических колебаниях равна:

.

Потенциальная энергия U тела, смещенного на расстояние х от положения равновесия, измеряется той работой, которую произведет возвращающая сила  , перемещая тело в положение равновесия.

                       

Кинетическая энергия



      Заменив в (1.5.2)   и сложив почленно уравнения кинетической и потенциальной энергии, получим выражение для полной энергии:



      Полная механическая энергия гармонически колеблющегося тела пропорциональна квадрату амплитуды колебания.

Вопрос 37 Затухающие колебания

Затухающие колебания – это колебания, амплитуда которых уменьшается с течением времени из-за потерь энергии в реальной колебательной системе.

Закон затухания колебаний определяется параметрами колебательной системы.

Амплитуда UЗ затухающих колебаний уменьшается с течением времени по экспоненте (пунктирная кривая на графиках колебаний таблицы 1).

Промежуток времени τ, в течение которого амплитуда колебаний уменьшается в е раз, называется временем релаксации.

Величина, обратная времени релаксации и определяемая параметрами колебательного контура, называется коэффициентом затухания δ:

. (1)

Затухание нарушает периодичность колебаний, поэтому затухающие колебания не являются периодическими и, строго говоря, к ним неприменимо понятие периода или частоты. Однако, если затухание мало, то можно условно пользоваться понятием периода как промежутка времени между двумя последующими максимумами (или минимумами) колеблющейся величины. Период затухающих колебаний Tз зависит от параметров колебательного контура (индуктивности L, ёмкости C и коэффициента затухания δ) и определяется по формуле: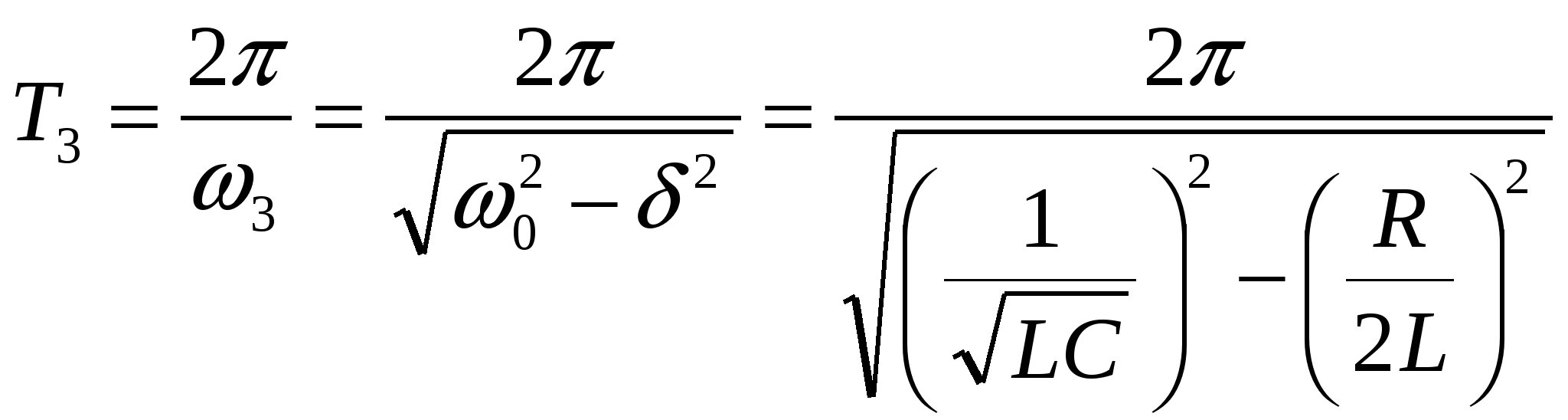

. (2)

При отсутствии потерь энергии (R=0  δ=0) формула для расчёта периода колебаний принимает вид (формула Томсона):

. (3)

Формула Томсона также применима и в том случае, когда циклическая частота собственных незатухающих колебаний ω0 во много раз больше коэффициента затухания δ .

Если U(t) и U(t+T) – амплитуды двух последующих колебаний, соответствующих моментам времени, отличающимся на период, то отношение

(4)

называется декрементом затухания, а логарифм отношения:

ln= æ (5)

– логарифмическим декрементом затухания.

Связь между коэффициентом затухания δ и логарифмическим декрементом затухания æ устанавливается следующим образом.

Амплитуды двух последующих колебаний можно представить в виде:

; (6)

Тогда отношение двух последующих амплитуд: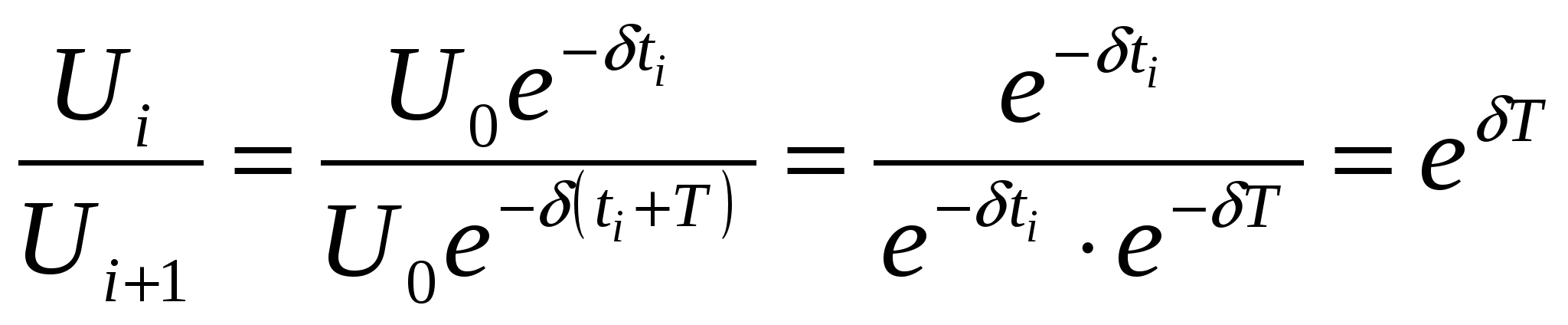

; (7)

а логарифм их отношения

ln= æ.

Вопрос 38 Вынужденные колебания

Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными.

В этом случае внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил трения.

Если свободные колебания происходят на частоте ω0, которая определяется параметрами системы, то установившиеся вынужденные колебания всегда происходят на частоте ω внешней силы.  Тогда уравнение вынужденных колебаний запишется в виде 

(**)

где  – собственная круговая частота свободных колебаний, ω – циклическая частота вынуждающей силы. В случае вынужденных колебаний груза на пружине (рис. 2.5.1) величина A определяется выражением: 

Установившиеся вынужденные колебания груза на пружине происходят на частоте внешнего воздействия по закону 

x (t) = xmcos (ωt + θ).

Амплитуда вынужденных колебаний xm и начальная фаза θ зависят от соотношения частот ω0 и ω и от амплитуды m>ymвнешней силы.

Если частота ω внешней силы приближается к собственной частоте ω0, возникает резкое возрастание амплитуды вынужденных колебаний. Это явление называется резонансом. Зависимость амплитуды xm вынужденных колебаний от частоты ω вынуждающей силы называется резонансной характеристикой или резонансной кривой.

Вынужденные колебания – это незатухающие колебания. Неизбежные потери энергии на трение компенсируются подводом энергии от внешнего источника периодически действующей силы

Вопрос 39 Гармонические волны. Уравнение бегущей волны. Фазовая скорость.

Волны, образованные внешним воздействием, приложенным к упругой среде, называются бегущими волнами: они “бегут” от создающего их источника. Если внешняя сила совершает гармонические колебания, то вызванные ею волны называются гармоническими бегущими волнами.

Фазовая скорость волны.

Фазовая скорость  - это скорость распространения данной фазы колебаний, т.е. скорость волны.

Связь длины волны , фазовой скорости  и периода колебаний Т задается соотношением:

.

Учитывая, что , где  - линейная частота волны,  - период, а циклическая частота волны , получим разные формулы для фазовой скорости:

.

Для волнового процесса характерна периодичность по времени и по пространству.

Т – период колебаний точек среды. Роль пространственного периода играет длина волны . Соотношение между периодом и циклической частотой задается формулой: . Аналогичное соотношение можно записать для длины волны и величиной k, называемой волновым числом: .

еще одно уравнение для фазовой скорости:

.

Фазовая скорость различна для разных сред. В случае упругих поперечных волн (в твердом теле) фазовая скорость равна:

 ,

где - модуль сдвига среды,  -ее плотность в невозбужденном состоянии (т.е. когда в этой среде не распространяется упругая волна).

Фазовая скорость упругих продольных волн в твердом теле равна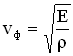

,

где Е - модуль Юнга, - плотность невозмущенной среды (твердого тела до момента распространения по нему волны).

Фазовая скорость продольных волн в жидкости и газе определяется соотношением: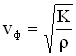

,

где К – модуль объемной упругости среды – величина, характеризующая способность среды сопротивляться изменению ее объема, - плотность невозмущенной среды.

Фазовая скорость продольных волн в идеальном газе задается формулой: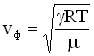

,

 - показатель адиабаты, - молярная масса, Т – абсолютная температура, R – универсальная газовая постоянная. Фазовая скорость в газе зависит от сорта газа () и от его термодинамического состояния (Т).

Уравнение бегущей волны. уравнение бегущей волны в одномерном пространстве, которое предполагаем изотропным и однородным. Кроме того, силы сопротивления в среде считаем пренебрежимо малыми (т.е. нет затухания колебаний). Пусть точка О - центр (источник) колебаний, она колеблется по закону:

,

где  - смещение точки О от положения равновесия, - частота, А – амплитуда колебаний. Часы или секундомер №1 включаются сразу, как только начинаются колебаний точки О, и отсчитывают время t (Рисунок 2.1.1). Ось ОУ совпадает с направлением распространения волны.

Через промежуток времени  процесс колебаний дойдет до точки В, и она будет колебаться по закону: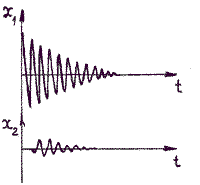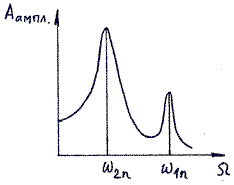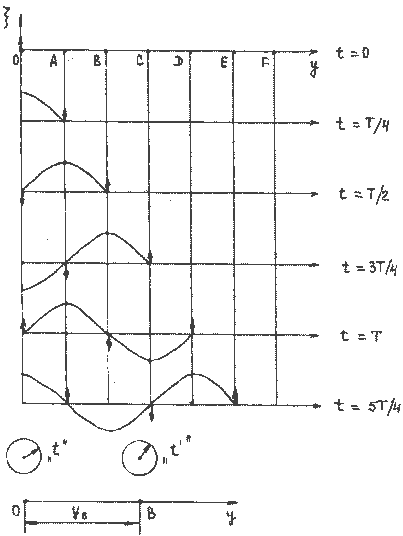

.




Амплитуда колебаний в случае отсутствия затухания процесса будет такой же как и амплитуда точки О. Часы или секундомер №2 включаются тогда, когда колебательный процесс дойдет до точки В (т.е. когда начинает колебаться точка В), и отсчитывают время . Моменты времени t и  связаны между собой соотношением  или . Расстояние между точками О и В обозначим . Фазовая скорость волны равна , тогда . Учитывая соотношения для  и  и формулы  и , можно записать уравнение колебаний точки В в разных видах: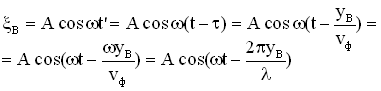

.

Аналогично уравнению колебаний точки В запишем уравнение колебаний любой точки среды, расположенной на расстоянии y от источника колебаний:

,

где  - волновое число (см. определение выше).

Это уравнение и есть уравнение для смещения  любой точки пространства в любой момент времени, т.е. уравнение бегущей волны, где А – амплитуда, величина  - фаза волны, которая в

Билет 40

СЛОЖЕНИЕ ВОЛН

Сложение в пространстве двух (или нескольких) волн, при котором образуется постоянное во времени распределение амплитуды результирующих колебаний в различных точках пространства, называется интерференцией.

СТОЯЧИЕ ВОЛНЫ

Частным случаем интерференции являются стоячие волны - волны, образующиеся при наложении двух бегущих волн, распространяющихся навстречу друг другу волн с одинаковыми амплитудами и частотами.

Для вывода уравнения стоячей волны примем: 1) волны распространяются в среде без затухания; 2) А₁ = А₂ =А - имеют равные амплитуды; 3) ω₁ = ω₂= ω - равные частоты; 4)φ₁₀ = φ₂₀ = 0.

Уравнение бегущей волны, распространяющейся вдоль положительного направления оси х (т.е. уравнение падающей волны):

(1)

Уравнение бегущей волны, распространяющейся в отрицательном направлении оси х (т.е. уравнение отраженной волны):

(2)

Сложив (1) и (2) получим уравнение стоячей волны: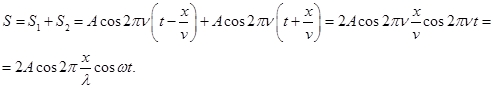



Особенностью  стоячей волны является то, что амплитуда зависит от координаты х. При перемещении от одной точки к другой амплитуда меняется по закону:



ДИСПЕРСИЯ И ГРУППОВАЯ СКОРОСТЬ ВОЛНЫ

Дисперсия волн - ,зависимость фазовой скорости гармонических волн в среде от частоты их колебаний. Дисперсия волн наблюдается для волн любой природы. Наличие дисперсии волн приводит к искажению формы сигнала (напр., звукового импульса) при распространении в среде. 

Групповая скорость - ,величина, приближенно характеризующая распространение негармонической волны (она является суперпозицией группы гармонических волн). Если форма волны изменяется в результате дисперсии волн в среде не очень быстро, то можно рассматривать распространение негармонической волны как целого с групповой скоростью, отличной от фазовых скоростей ее гармонических составляющих. Групповая скорость характеризует скорость переноса энергии волной. 

Билет 41

ИНТЕРФЕРЕНЦИЯ СВЕТА

Интерференция - явление, имеющее место при наложении (суперпозиции) когерентных волн и состоящее в увеличении амплитуды результирующих колебаний в одних точках пространства при одновременном ослаблении колебаний в других точках. Таким образом, при интерференции происходит пространственное перераспределение энергии накладывающихся волн.

Интерференция света - частный случай общего явления интерференции волн. При интерференции света возникает интерференционная картина - чередование областей с повышенной и пониженной освещенностью, например, кольца Ньютона, наблюдаемые в данной работе. Устойчивая интерференция возможна лишь в случае, когда в любой точке области наложения волн их разность фаз постоянна во времени (волны взаимно когерентны).

РАСЧЁТ ИНТЕРФЕРЕНЦИОННОЙ КАРТИНЫ ОТ ДВУХ КОГЕРЕНТНЫХ ИСТОЧНИКОВ

Пусть в некоторую точку пространства M приходят световые волны от двух взаимно когерентных источников 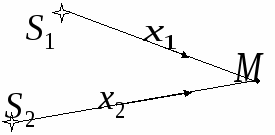и (рисунок 1), или, что равноценно, от одного источника, но прошедшие до места встречи разные пути. Через и обозначим оптические пути, пройденные волнами от источников до точки : , где - расстояния, пройденные волнами, - показатели преломления сред, через которые шли волны.


Рисунок 1 - Ход лучей при интерференции.


В точке M каждая из этих волн вызывает колебания напряженности электрического поля, описывающиеся уравнениями:

, , (1)

где - мгновенные значения напряженностей электрических полей обеих волн, - амплитуды напряженностей, - циклическая частота, - время, - волновое число, - длина световой волны в вакууме, - начальные фазы волн (для упрощения далее полагаем, что ).

Амплитуда результирующего колебания в точке такова:

, (2)

где - разность фаз волн в точке M; - оптическая разность хода волн.

Из формулы (2) следует, что волны усилят друг друга, и в точке возникнет интерференционный максимум освещенности, если , то есть , где , или , следовательно:

. (3)

Последнее равенство есть условие интерференционного максимума: две волны при наложении усилят друг друга, если их оптическая разность хода равна нулю или на ней укладывается целое число длин волн . В этом случае , а если , то .

Из (2) также следует, что взаимное ослабление волн и образование в точке интерференционного минимума имеет место, если , то есть , где . При этом , то есть:

. (4)

Последнее равенство есть условие интерференционного минимума: две волны при наложении ослабят друг друга, если на оптической разности хода укладывается нечетное число длин полуволн . В этом случае , а при происходит полное гашение: .

БИЛЕТ 42

ПОЛОСЫ РАВНОЙ ТОЛЩИНЫ И РАВНОГО НАКЛОНА

Различают интерференционные картины двух типов: полосы равного наклона, когда на плоскопараллельный слой падает расходящийся пучок лучей, и полосы равной толщины, когда пучок параллельных лучей падает на слой с непараллельными поверхностями (клин).

Частным случаем полос равной толщины являются кольца Ньютона. Для их наблюдения плосковыпуклую линзу с большим радиусом кривизны 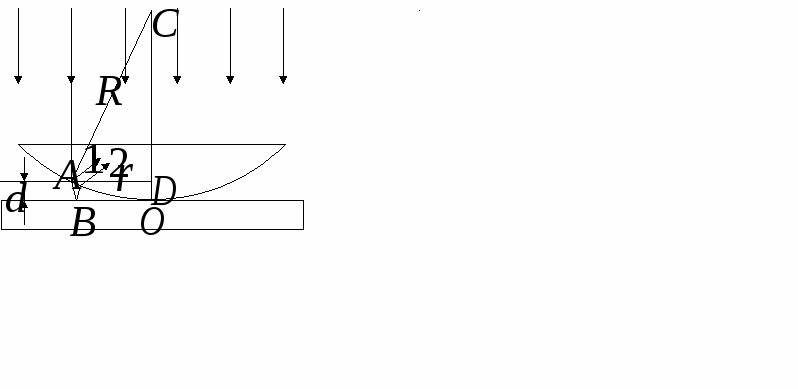помещают на гладкую стеклянную пластину (см. рисунок 2). Между линзой и пластиной вокруг точки их соприкосновения имеется тонкий воздушный клин. На линзу направляют пучок параллельных лучей. В отраженном свете полосы равной толщины возникают в результате интерференции луча 1, отраженного в точке от нижней поверхности линзы, и луча 2, отраженного в точке от верхней поверхности пластинки, то есть от поверхностей воздушного клина. Ввиду малости кривизны линзы лучи 1 и 2 фактически совпадают и накладываются на падающий луч (на рисунке 2 углы отражения лучей 1 и 2 преувеличены для наглядности). Толщина воздушного зазора определяется расстоянием до точки касания, поэтому полосы равной толщины имеют вид концентрических колец.





Рисунок 2 - Ход лучей при наблюдении колец Ньютона.

Как видно из рисунка 2, оптическая разность хода лучей 1 и 2 такова:

, (5)

( добавляется вследствие потери полуволны при отражении света от оптически более плотной среды в точке B). Поскольку клин воздушный, то . Выведем формулу, связывающую радиус темного кольца номер , радиус кривизны линзы и длину световой волны . Соединим центр кривизны линзы C с точками A и O. Для прямоугольного треугольника ACD имеем:

.

Пренебрежем величиной ввиду ее малости () и получим , откуда . Подставляя это выражение для в формулу (5), получаем:

. (6)

Темные кольца проходят там, где величина удовлетворяет условию минимума (4). Приравняем правые части равенств (4) и (6):

.

и получим из последнего равенства формулу для радиусов темных колец в отраженном свете:

. (7)

БИЛЕТ 43

принцип Гюйгенса-Френеля

В соответствии с принципом Гюйгенса-Френеля каждая щель дифракционной решетки становится источником вторичных волн. Следовательно, решетку можно представить как набор когерентных источников, расположенных в щелях решетки и испускающих световые лучи, отклоняющиеся вправо и влево от первоначального направления на различные углы в пределах от 0 до 90°.

В фокальной плоскости линзы, помещенной за решеткой, наблюдается дифракционная картина, обусловленная двумя факторами: дифракцией света от каждой щели и многолучевой интерференцией света от всех щелей.





Рисунок 1 - Ход лучей в дифракционной решетке. 1 – дифракционная решетка, 2 – собирающая линза, 3 – экран.

максимумы будут наблюдаться под углами , определяемыми следующим условием (формулой дифракционной решетки):

(1)

где - номер максимума или порядок спектра.
Формула для нахождения длин световых волн

.

ДИФРАКЦИЯ ФРЕНЕЛЯ НА КРУГЛОМ ОТВЕРСТИИ

 Весь фронт волны  разбивается на бесконечное количество узких колечек. Сумма изображается на графике –в пределе  получается спираль (рис.4).



 

  

        Действие отверстия в точке наблюдения, находящейся на оси картины,  зависит от того, сколько зон Френеля укладывается в отверстии. Если число зон нечетное – действие больше, чем без экрана. Больше всего – если открыта одна зона. Если открыта только первая зона, то, как видно из рисунка, амплитуда примерно в два раза больше, чем если бы был открыт весь фронт, а интенсивность – в четыре раза больше. Если открыто четное число зон – меньше, чем без экрана. Меньше всего – если открыты 2 зоны. Это все хорошо видно из графического рассмотрения (рис.4). Амплитуда определяется как длина вектора  ON с началом в точке О, а конец – там, где кончается последняя открытая зона. Вокруг центральной точки будут темные и светлые кольца – это ясно из осевой симметрии картинки.

БИЛЕТ 44

ДИФРАКЦИЯ ФРАУНГОФЕРРА НА ЩЕЛИ И ДИФРАКЦИОННОЙ РЕШЁТКЕ

Дифракция Фраунгофера — случай дифракции, при котором дифракционная картина наблюдается на значительном расстоянии от отверстия или преграды. 

Оптическая разность хода волн, идущих от краев щели в произвольном направлении , равна

 

.                                       (1.9)

 

После прохождения через линзу Л они собираются на экране в точке Р и интерферируют. Для выяснения вида интерференционной картины разобьем открытую поверхность волнового фронта АВ на зоны Френеля (разность хода от краев соседних зон равна ), параллельные краям щели. Всего на ширине  щели уместится

 

  зон.                               (1.10)



Так как на щель падает плоская волна, то площади всех зон одинаковы,  значит, одинакова амплитуда колебаний, возбуждаемых в точке Р действием каждой зоны Френеля, а фазы колебаний, создаваемых соседними зонами, противоположны. Следовательно, колебания каждой пары соседних зон будут гасить друг друга.

Поэтому, если на ширине щели укладывается четное число зон Френеля, то амплитуда результирующего колебания в точке Р равна 0 и наблюдается минимум интенсивности света.

Из (1.10) следует условие образования дифракционного минимума:

 

 (k=1,2,…)                      (1.11)

 

Дифракционный максимум возникает при нечетном числе зон Френеля, укладывающихся на ширине щели

 

 (k=1,2,…),                       (1.12)

Одномерная дифракционная решетка – это система параллельных щелей равной ширины а, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками b. Величина

 

                                      (1.15)

 

называется постоянной (периодом) дифракционной решетки.

При падении на решетку плоской монохроматической волны в фокальной плоскости линзы наблюдается дифракционная картина.

Она является результатом двух процессов: дифракции света от каждой щели и интерференции пучков света, дифрагированных от всех щелей. Для выяснения характера картины на экране рассмотрим дифракцию от двух щелей (рис5). Очевидно, что в тех направлениях,  в которых ни

одна из щелей не распространяет света, он не будет распространяться и при двух щелях, т.е. прежние минимумы интенсивности будут возникать в направлениях, определяемых условием (1.11)

 

 (k=1,2,…).

 

Кроме того, в некоторых других направлениях вторичные волны, идущие от двух щелей, будут гасить друг друга вследствие интерференции, т.е. будут наблюдаться дополнительные минимумы. Они возникают в направлениях, отвечающих условию

 

        (m=0,1,2,…),               (1.16)

 

где  - разность хода лучей, идущих от краев А и В щелей. Действие одной щели будет усиливать действие другой, если в разности хода укладывается целое число длин волн:

 

 (m=0,1,2,…).            (1.17)

 

Формула (1.17) – условие образования главных максимумов.

БИЛЕТ 45

ДИФРАКЦИЯ НА ПРОСТРАНСТВЕННОЙ РЕШЁТКЕ. ФОРМУЛА ВУЛЬФА-БРЭГТА.

Дифракционную картину могут дать не только рассмотренные выше одномерные структуры, но также двумерные и трехмерные периодические структуры, например, кристаллические тела. Однако период кристаллических тел d мал, составляет единицы ангстрем (1 =10^-4 мкм), т.е. значительно меньше длин волн видимого света (0,4-0,8 мкм). Поэтому для видимого света кристаллы являются однородной средой, и дифракция не наблюдается.

Вто же время для значительно более коротковолнового рентгеновского излучения( 10-9 - 10-11 м) кристаллы представляют собой естественные дифракционные решетки (см. рис.6). Абсолютный показатель преломления рентгеновского излучения близок к единице, поэтому оптическая разность хода между лучами

Рис.6

1- и 2-, отражающимися от кристаллографических плоскостей CD+DE=2dsin, где d - расстояние между плоскостями, в которых лежат узлы (атомы) кристаллической решетки,  - угол скольжения лучей.

Условию интерференционных максимумов удовлетворяет [см.(3,15)] формула Вульфа-Брэгга

2dsin =m , m=1,2,3- (13)

где m - порядок дифракционного максимума.

МЕТОД ДЕБАЯ - ШЕРРЕРА

Метод Дебая — Шеррера - один из методов рентгеноструктурного анализа. Также называется методом порошка.

Монохроматический пучок рентгеновского излучения, направляется на образец исследуемого материала, растертого в порошок. На фотопленке, свернутой цилиндром вокруг образца, изображение (дебаеграмма) получается в виде колец. Расстояние между линиями одного и того же кольца на дебаеграмме позволяет найти брэгговские углы отражения. Затем, по формуле Брэгга - Вульфа  можно получить отношение  расстояния между отражающими плоскостями к порядку отражения.