|
|
Вопрос1 Статистическая обработка результатов эксперимента
Вопрос№1) Статистическая обработка результатов эксперимента
Методами статистической обработки результатов называются математические приемы, формулы, способы количественных расчетов, с помощью которых показатели, получаемые в ходе эксперимента, можно обобщать, приводить в систему, выявляя скрытые в них закономерности. Речь идет о таких закономерностях статистического характера, которые существуют между изучаемыми в эксперименте переменными величинами
1)Получение первичной числовой информации
На данном этапе, исходя из разработанной модели исследуемого педагогического процесса, необходимо установить количество оцениваемых параметров, методы их получения и оценивания, а также критерии выставления оценок и их шкалы.
2)Обработка полученных результатов с помощью
методов математической статистики
Выполнение данного этапа представляет собой техническую работу по проведению расчетов по формулам и процедурам, разработанным специалистами в области математической статистики. Однако следует обращать особое внимание на обоснование применимости тех или иных математических методов. К числу наиболее эффективных методов математической статистики, которые целесообразно использовать в методике преподавания физики, следует отнести:
первичную обработку результатов: формирование упорядоченных массивов, получение обобщающих характеристик (размах выборки, медиана, средние значения, дисперсия и т.д.), построение выборочных гистограмм;
оценивание параметров полученных распределений (при необходимости, с построением доверительных интервалов);
регрессионный анализ, позволяющий установить наличие зависимостей между различными характеристиками испытуемых групп, а также вид этих зависимостей;
сравнение выборок, полученных по различным группам, установление различий между ними, определение значимости полученных различий.
Указанные выше математические методы являются достаточно формальными до тех пор, пока полученные на их основе численные значения, графики, гистограммы не получат наглядный вид и не будут обоснованно интерпретированы. Эта часть работы является наиболее сложной и дискуссионной, требующей от учителя физики определенного опыта.
Вопрос№2)Кинематика материальной точки
Кинематика – раздел механики. который изучает различные типы движения без рассмотрения причин вызывающих это движение.
Движение любого объекта в кинематике изучают по отношению к некоторой системе отсчета, включающей:
тело отсчета;
систему измерения положения тела в пространстве (систему координат);
прибор для измерения времени (часы например).
Основные кинематические понятия.
Материальная точка(М.Т.) — тело, размерами которого по сравнению с характерными расстояниями данной задачи можно пренебречь. При поступательном движении в ряде случаев при помощи понятия М. Т. можно описывать и изменение положения более крупных объектов. Так, например, тепловоз, проходящий расстояние 1 метр, может считаться М. Т., поскольку его ориентация относительно системы координат в процессе движения является фиксированной и не влияет на постановку и ход решения задачи.
Радиус-вектор — вектор, определяющий положение материальной точки в пространстве: 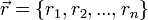 . Здесь — координаты радиус-вектора. Геометрически изображается вектором, проведенным из начала координат к материальной точке. Зависимость радиус-вектора (или его координат ) от времени называется законом движения.
Траектория — воображаемая линия, описываемая концом радиус-вектора в процессе движения. Иными словами, траектория — это линия вдоль которой движется материальная точка. При этом закон движения выступает как уравнение, задающее траекторию параметрически. Длину участка траектории между начальным и конечным моментами времени часто называют пройденным расстоянием, длиной пути или путем и обозначают буквой S. При таком описании движения S выступает в качестве обобщенной координаты, а законы движения в этом случае записывается в виде S = S(t) и аналогичны соответствующим законам для координат. Например закон равноускоренного криволинейного движения может быть записан в виде:
 ,
Где : — модуль начальной скорости, а — Тангенциальное ускорение.
|
|
|
Скачать 6.64 Mb.