Вопрос1 Статистическая обработка результатов эксперимента

• Название: Вопрос1 Статистическая обработка результатов эксперимента
• Анкор: fizika.doc
• Дата: 16.01.2018
• Размер: 6.64 Mb.
• Имя файла: fizika.doc
• Тип: Документы; #14141
• страница: 10 из 12

Волновая функция лишь приписывается, сопоставляется движущейся частице, как функция, определенным образом характеризующая, отображающая состояние ее движения, позволяющая предсказывать дальнейший характер и характеристики движения. То, что такое предсказание является неоднозначным, вероятностным, свидетельствует об ограниченности привычного для макромира и классической механики однозначного детерминизма. В микромире однозначно предсказываются лишь вероятности тех или иных значений координаты и импульса движущейся частицы.

Вопрос№52

Стационарным состоянием называется состояние квантовой системы, при котором её энергия и другие динамические величины, характеризующие квантовое состояние, не изменяются.

На основе полученных данных, Н. Бором в 1916 г. сформулировал свои постулаты. Согласно его выводам, атом может переходить из одного стационарного состояния в другое лишь с помощью поглощения или выделения кванта с энергией, равной разности энергий атома в начальном и конечном стационарных состояниях. Квантовая теория стационарных состояний была разработана Эрвином Шрёдингером в 1925 году.

Основное уравнение должно быть уравнением относительно волновой функции Ψ(х, у, z, t), так как именно она, или, точнее, величина |Ψ|², определяет вероятность пребывания частицы в момент времени t в объеме ΔV, т. е. в области с координатами х и х + dх, у и у + dу, z и z + dz.

Основное уравнение нерелятивистской квантовой механики сформулировано в 1926 г. Э. Шредингером. Уравнение Шрёдингера, как и все основные уравнения физики (например, уравнения Ньютона в классической механике и уравнения Максвелла для электромагнитного поля), не выводится, а постулируется. Правильность этого уравнения подтверждается согласием с опытом получаемых с его помощью результатов, что, в свою очередь, придает ему характер закона природы. Общее уравнение Шредингера имеет вид

, (1)

где ħ = h / (2π), m – масса частицы, Δ – оператор Лапласа , i – мнимая единица, U(x, y, z, t) – потенциальная функция частицы в силовом поле, в котором она движется, Ψ(x, y, z, t) – искомая волновая функция частицы.

Уравнение (1) справедливо для любой частицы (со спином, равным 0), движущейся с малой (по сравнению со скоростью света) скоростью, т. е. со скоростью υ«с. Оно дополняется условиями, накладываемыми на волновую функцию:

1) волновая функция должна быть конечной, однозначной и непрерывной;

2) производные должны быть непрерывны;

3) функция |Ψ|² должна быть интегрируема (это условие в простейших случаях сводится к условию нормировки вероятностей ).

Уравнение (1) называют уравнением Шредингера, зависящим от времени.

Дли многих физических явлений, происходящих в микромире, уравнение (1) можно упростить, исключив зависимость Ψ от времени, т.е. найти уравнение Шредингера для стационарных состояний – состояний с фиксированными значениями энергии. Это возможно, если силовое поле, в котором частица движется, стационарно, т. е. функция U = U (х, у,z)не зависит явно от времени и имеет смысл потенциальной энергии. В данном случае решение уравнения Шредингера может быть представлено в виде
. (2)

Уравнение (2) называется уравнением Шредингера для стационарных состояний.

В это уравнение в качестве параметра входит полная энергия Е частицы. В теории дифференциальных уравнений доказывается, что подобные уравнения имеют бесчисленное множество решений, из которых посредством наложения граничных условий отбирают решения, имеющие физический смысл. Для уравнения Шредингера такими условиями являются условия регулярности волновых функций: вол новые функции должны быть конечными, однозначными и непрерывными вместе со своими первыми производными. Таким образом, реальный физический смысл имеют только такие решения, которые выражаются регулярными функциями Ψ. Но регулярные решения имеют место не при любых значениях параметра Е, а лишь при определенном их наборе, характерном для данной задачи. Эти значения энергии называются собственными. Решения, которые соответствуют собственным значениям энергии, называются собственными функциями. Собственные значения Е могут образовывать как непрерывный, так и дискретный ряд. В первом случае говорят о непрерывном, или сплошном, спектре, во втором – о дискретном спектре.


Тунне́льный эффект, туннели́рование — преодоление микрочастицей потенциального барьера в случае, когда её полная энергия (остающаяся при туннелировании неизменной) меньше высоты барьера. Туннельный эффект — явление исключительно квантовой природы, невозможное в классической механике и даже полностью противоречащее ей. Аналогом туннельного эффекта в волновой оптике может служить проникновение световой волны внутрь отражающей среды (на расстояния порядка длины световой волны) в условиях, когда, с точки зрения геометрической оптики, происходит полное внутреннее отражение. Явление туннелирования лежит в основе многих важных процессов в атомной и молекулярной физике, в физике атомного ядра, твёрдого тела и т. д.

Коэффициент туннелирования (прохождения, просачивания) частицы через барьер D равен:

D=e(-2a/ ћ)(2m(U0-E))½ (1)

где а – ширина барьера, U0 – высота барьера, Ћ - постоянная Планка

В классической механике частица с энергией E < V0 не сможет вылететь из потенциальной ямы и будет всё время двигаться в ограниченной области пространства внутри ямы; устойчивому равновесию отвечает положение частицы на "дне" ямы (оно достигается при кинетической энергии частицы Екин = E — V = 0). Если же E > V0, то частица преодолеет действие сил притяжения и покинет яму. Примером может служить движение упругого шарика, находящегося в поле сил земного притяжения, в чашке с пологими стенками (рис. 2).
Уравнение для полной энергии частицы, движущейся в потенциальной яме с непроницаемыми стенками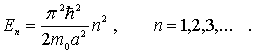

     

волновые функции частицы в одномерной потенциальной яме с бесконечно высокими стенками имеют вид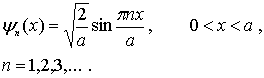

     

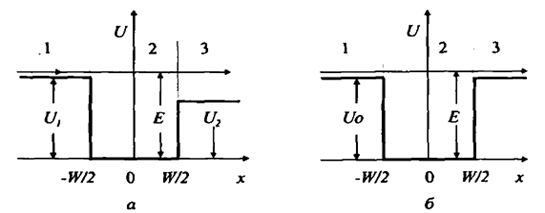
Вероятность того, что частица в яме находится в области  , определяется выражением

БИЛЕТ 53

Стационарным состоянием (от лат. stationarius — стоящий на месте, неподвижный) называется состояние квантовой системы, при котором её энергия и другие динамические величины, характеризующие квантовое состояние, не изменяются.

На основе полученных данных, Н. Бором в 1916 г. сформулировал свои постулаты. Согласно его выводам, атом может переходить из одного стационарного состояния в другое лишь с помощью поглощения или выделения кванта с энергией, равной разности энергий атома в начальном и конечном стационарных состояниях.^[1] Квантовая теория стационарных состояний была разработана Эрвином Шрёдингером в 1925 году.


Стационарные чистые состояния в квантовой механике описываются волновой функцией



где  подчиняется стационарному уравнению Шрёдингера

Квадрат модуля волновой функции

не зависит от времени.

В развитие идеи де Бройля о волновых свойствах частиц Шредингер в 1926 г. получил уравнение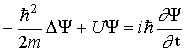

 (20)

где m - масса частицы,  - мнимая единица, U - потенциальная энергия частицы, D - оператор Лапласа [ см. (1.10)].

Решение уравнения Шредингера позволяет найти волновую функцию Y(x, y, z, t) частицы, которая описывает микросостояние частицы и ее волновые свойства.

Если поле внешних сил постоянно во времени (т.е. стационарно), то U не зависит явно от t. В этом случае решение уравнения (20) распадается на два множителя

Y(x, y, z, t) =y(x, y, z) exp[-i(E/)t] (21)

где E/=w.

В стационарном случае уравнение Шредингера имеет вид

 (22)

где Е, U - полная и потенциальная энергия, m - масса частицы.

Следует заметить, что исторически название "волновой функции" возникло в связи с тем, что уравнение (20) или (22), определяющее эту функцию, относится к виду волновых уравнений.

Туннельный эффект (туннелирование) – прохождение частицы (или системы) сквозь область пространства, пребывание в которой запрещено классической механикой. Наиболее известный пример такого процесса – прохождение частицы сквозь потенциальный барьер, когда её энергия Е меньше высоты барьера U₀. В классической физике частица не может оказаться в области такого барьера и тем более пройти сквозь неё, так как это нарушает закон сохранения энергии. Однако в квантовой физике ситуация принципиально другая. Квантовая частица не движется по какой-либо определенной траектории. Поэтому можно лишь говорить о вероятности нахождения частицы в определенной области пространства ΔрΔх > ћ. При этом ни потенциальная, ни кинетическая энергии не имеют определенных значений в соответствии с принципом неопределенности. Допускается отклонение от классической энергии Е на величину ΔЕ в течение интервалов времени t, даваемых соотношением неопределённостей ΔЕΔt > ћ (ћ = h/2π, где h – постоянная Планка).

     Возможность прохождения частицы сквозь потенциальный барьер обусловлена требованием непрерывной волновой функции на стенках потенциального барьера. Вероятность обнаружения частицы справа и слева связаны между собой соотношением, зависящим от разности E - U(x) в области потенциального барьера и от ширины барьера x₁ - x₂ при данной энергии.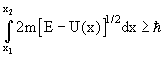



    С увеличением высоты и ширины барьера вероятность туннельного эффекта экспоненциально спадает. Вероятность туннельного эффекта также быстро убывает с увеличением массы частицы.
    Проникновение сквозь барьер носит вероятностный характер. Частица с Е < U₀, натолкнувшись на барьер, может либо пройти сквозь него, либо отразиться. Суммарная вероятность этих двух возможностей равна 1. Если на барьер падает поток частиц с Е < U₀, то часть этого потока будет просачиваться сквозь барьер, а часть – отражаться. Туннельное прохождение частицы через потенциальный барьер лежит в основе многих явлений ядерной и атомной физики: альфа-распад, холодная эмиссия электронов из металлов, явления в контактном слое двух полупроводников и т.д.

БИЛЕТ 54

 Частица в прямоугольной потенциальной яме

При выращивании пленки узкозонного полупроводника между двумя слоями широкозонного материала может быть реализован потенциальный рельеф, показанный на рис. 1.4.

Рис. 4. Энергетическая диаграмма прямоугольной потенциальной ямы

 

В этом случае задача определения стационарных состояний движения электрона сводится к задаче о поведении частицы в пря­моугольной потенциальной яме.

Для асимметричной потенциальной ямы (рис. 1.4, а) с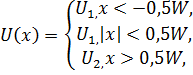



при E< U₂ общие решения уравнения (1.1.2) в областях 1 - 3 (с по­стоянными значениями потенциала) можно представить в виде

 Частица в одномерной прямоугольной "потенциальной яме"

Такая "яма" описывается потенциальной энергией вида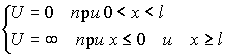



При таком условии частица не проникает за

пределы "ямы", т.е. y(0)=y(l)=0.(27)

В пределах ямы (0 уравнение (22) сведется к уравнению

или(28)

где k²=. Общее решение (28)

y(х)=Аsinkx+Bcoskx (29)

Так как согласно (27) ψ(0)=0,то В=0, тогда

y(х)=Аsinkx .(30)

Условие (27) y(l)=Аsinkl=0выполняется только при kl=pn,где n=1,2...целые числа, т.е. необходимо, чтобы

k=pn/l.(31)

Из (29) и (31) следует, что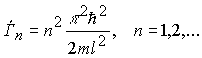

 (32)

Таким образом, энергия в "потенциальной яме" принимает лишь определенные, дискретные значения, т.е. квантуется. Квантованные значения энергии Е_nназываются уровнями энергии, а числоn, определяющее энергетические уровни, называется главным квантовым числом.

обственные значения энергии W частицы в одномерной потенциальной яме бесконечной глубины : W = n²h²/2mL², где n=(1,2,..). Квантованные значения Wn называются уровнями энергии, а числа n - квантовыми числами.

ИМПУЛЬС частицы

    Полная энергия и импульс частицы определяются соотношениями

E = mc²γ,

p = γmv = vE/c².

    Полная энергия и импульс частицы зависят от системы отсчетаю. Масса не меняется при переходе от одной инерциальной системы отсчета к другой. Она является лоренцевым инвариантом. Полная энергия импульс и масса связаны соотношением

E² - p²c² = m²c⁴,

где E, р и  m - полная энергия, импульс и масса частицы, с - скорость света в вакууме. Из соотношения (3) и (4) следует, что если энергия E и импульс p измеряются в двух различных системах движущихся друг относительно друга со скоростью v, то энергия  и импульс   будут иметь в этих системах различные значения. Однако величина E² - p²c², которая называется релятивистский инвариант, будет в этих системах одинаковой. 
    Полная и кинетическая энергия связаны между собой соотношением

Е =  T + Е₀ = Т + mc², Т = Е - mc²,  

где T - кинетическая энергия частицы, Е₀ - энергия покоя частицы.
Из (4) и (5) можно получить соотношение связывающее импульс p и кинетическую энергию T частицы

p = (T² + 2Tmc²)^1/2/c.

Можно выделить два предельных случая
1. Ультрарелятивистский. Кинетическая энергия частицы много больше ее энергии покоя

T >> mc²  p = T/c или T = cp.

2. Классический. Кинетическая энергия частицы много меньше ее энергии покоя

T << mc²  p = (2Tm)^1/2 или T = p²/2m.

2. Электрон способен переходить с одной стационарной орбиты на другую. Только в этом случае он испускает или поглощает определенную порцию энергии монохроматического излучения определенной частоты. Эта частота зависит от уровня изменения энергии атома при таком переходе. 
Эти постулаты Бор использовал для расчета простейшего атома (водорода), рассматривая первоначально наиболее простую его модель: неподвижное ядро, вокруг которого по круговой орбите вращается электрон. Объяснение спектра водорода было большим успехом теории Бора.

Энергетический интервал между двумя уровнями энергии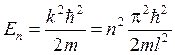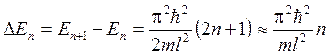

 ,

при l = 10^{-1 м мало, энергетические уровни расположены тесно} - непрерывное распределение энергии;

при l = 10^-10 м велико, энергия дискретна - линейчатый спектр.

Законы квантовой механики при больших значениях квантовых чисел должны переходить в законы классической физики.

55 БИЛЕТ

Гармонический осциллятор в кванто­вой механике — квантовый осциллятор —

описывается уравнением Шредингера (217.5), учитывающим выражение (222.1) для потенциальной энергии. Тог­да стационарные состояния квантового осциллятора определяются уравнением Шредингера вида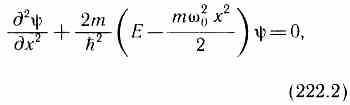



где Е — полная энергия осциллятора. В теории дифференциальных уравнений доказывается, что уравнение (222.2) ре­шается только при собственных значениях энергии

E_n=(n+¹/₂)h₀. (222.3)

Формула (222.3) показывает, что энергия квантового осциллятора может иметь лишь дискретные значения, т. е. квантует­ся. Энергия ограничена снизу отличным от нуля, как и для прямоугольной «ямы» с бесконечно высокими «стенками» (см. §220), минимальным значением энер­гии E₀=¹/₂h₀. Существование минималь­ной энергии — она называется энергией нулевых колебаний — является типичной для квантовых систем и представляет со­бой прямое следствие соотношения неоп­ределенностей.

Наличие нулевых колебаний означает, что частица не может находиться на дне «потенциальной ямы», причем этот вывод не зависит от ее формы. В самом деле, «падение на дно ямы» связано с обраще­нием в нуль импульса частицы, а вместе с тем и его неопределенности. Тогда не­определенность координаты становится сколь угодно большой, что противоречит, в свою очередь, пребыванию частицы в «потенциальной яме».

Вывод о наличии энергии нулевых ко­лебаний квантового осциллятора противо­речит выводам классической теории, со­гласно которой наименьшая энергия, кото­рую может иметь осциллятор, равна нулю (соответствует покоящейся в положении равновесия частице). Например, классиче­ская физика приводит к выводу, что при

T=0 энергия колебательного движения атомов кристалла должна обращаться в нуль. Следовательно, должно исчезать и рассеяние света, обусловленное колеба­ниями атомов. Однако эксперимент пока­зывает, что интенсивность рассеяния света при понижении температуры не равна ну­лю, а стремится к некоторому предельному значению, указывающему на то, что при Т ->0 колебания атомов в кристалле не прекращаются. Это является подтвержде­нием нулевых колебаний.

Из формулы (222.3) также следует, что уровни энергии линейного гармонического осциллятора расположены на одинаковых расстояниях друг от друга (рис.300), а именно расстояние между соседними энергетическими уровнями равно h₀, причем минимальное значение энергии

E₀=¹/₂h₀.

Строгое решение задачи о квантовом осцилляторе приводит еще к одному зна­чительному отличию от классического рас­смотрения. Квантово-механический расчет показывает, что частицу можно обнару­жить за пределами дозволенной области |х|x_max (см. рис. 16) в то время как с классической точки зрения она не может выйти за пределы области (-х_max, +x:_max). Таким образом, имеется отличная от нуля вероятность обнаружить частицу в той области, которая является классически запрещенной. Этот результат (без его вы­вода) демонстрируется на рис. 301, где приводится квантовая плотность вероят­ности wобнаружения осциллятора для состояния п=1. Из рисунка следует, что для квантового осциллятора действитель-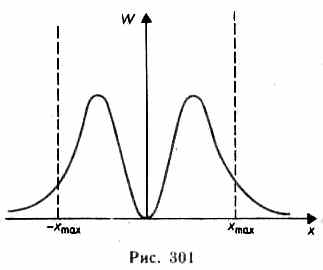



но плотность вероятности w имеет конеч­ные значения за пределами классически дозволенной области |х|x_max, т. е. имеет­ся конечная (но небольшая) вероятность обнаружить частицу в области за предела-

ми «потенциальной ямы». Существование отличных от нуля значений wза предела­ми «потенциальной ямы» объясняется воз­можностью прохождения микрочастиц сквозь потенциальный барьер (см. §221).