Квалиметрия - лекции. Введение. Понятие качества
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
2.6. Способы определения коэффициентов весомости2.6.1 Требования к балльным оценкам весомости
Это означает, что операция назначения баллов должна обеспечивать равенство психофизиологически определяемых расстояний между ними.
Способ назначения баллов должен быть таким, чтобы можно было проверить, что эксперт действительно уверен в своей оценке. Для этого при опросе эксперта применяют контрольную операцию, которая позволяет эксперту с других позиций взглянуть на сравниваемые объекты и вновь выразить свои ощущения.
Способ назначения баллов должен быть таким, чтобы при его повторении другим экспертом были получены те же или достаточно близкие оценки. 2.6.2 Общий порядок определения коэффициентов весомости
Нормирование: 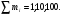 где 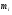 - сумма коэффициентов на данном уровне - сумма коэффициентов на данном уровне3 способа определения коэффициентов весомостей: 1. способ вспомогательной шкалы 2. способ парных сравнений 3. стоимостной способ 2.7 Экспертные кривые Экспертные кривые – это графики, изображающие зависимость между значениями 2-х показателей, построенные на основе экспертных суждений. Они предназначены для того, чтобы дать наглядную интерпретацию анализируемого явления, выявить характерные элементы анализируемой зависимости и найти параметры этих характерных элементов. 2.7.1 Кривые полезности (желательности) Эти кривые применяют для отображения уровня удовлетворения некоторой потребности субъекта в зависимости от значения анализируемого показателя. Пример Пусть разрабатывается конструкция нового строительного механизма. Требуется изобразить желательность для оператора усилий при перемещении рычага управления. 4 балла – оптимальные усилия; 1 балл – неприемлемые усилия. 4 3 2 1 10 20 30 40 усилия, Н желательность Задача анализа сводится к поиску характерных элементов (ХЭ). Можно выявить два характерных элемента:
Изготовителю важно обеспечить, чтобы усилия укладывались в ширину плато, если это невозможно, то выгоднее смещать усилия в большую сторону, так как снижение оценки желательности здесь происходит медленнее. 2.7.2 Кривые безразличия Их проводят в системе координат, образованной двумя показателями так, чтобы соединить точки, соответствующие равнопредпочтительными комбинациями значений показателей. По одну сторону от кривой оказывается сочетание значений, каждый из которых предпочтительнее любого сочетания, находящиеся по другую сторону. Назначение кривых безразличия: сравнение объектов, нахождение оптимальных комбинаций показателей. Пример Пусть разрабатывается конструкция мотора для прогулочного катера. Рассматривается два показателя: масса мотора m, максимальная скорость катера vmax. Масса может изменяться от 80 до 160 кг, максимальная скорость катера – от 20 до 60 км/ч. Оптимальной считается скорость 30-35 км/ч. Эта величина оценивается в 4 балла. Но она справедлива для массы 80 кг (min). Если v=30-35 км/ч и m=100, то присваивается 3,5 балла и т.д. 20 160 m vmax 140 40 30 50 60 120 100 80 A Б опт 1 2 3 4 Можно сравнивать конструкции: А лучше Б. 2.7.3 Обработка индивидуальных графиков Обобщение индивидуальных графиков, построенных экспертами, допустимо при соблюдении следующих 2-х условий:
Причины рассогласованности экспертных кривых:
В этом случае обобщение его индивидуального графика недопустимо. Иногда еретический график отбрасывают, либо проводят обсуждение полученных расхождений в составе экспертной группы. Пример Кривые желательности и усилий при перемещении рычага управления. 10 20 30 40 50 1 2 3 4 0 желательность усилие, Н 5 - 1 - 2 - 3 - 4 - Эксперты: Анализируем первых четырех экспертов, у их графиков есть общие ХЭ.
5-й эксперт имеет новый ХЭ по сравнению с первыми 4-мя экспертами: у него отличается кривизна кривой на спадающем участке. Его график еретический, поэтому нельзя использовать для построения обобщенного. Обобщать можно только первые 4 графика. 10 20 30 40 50 1 2 3 4 0 желательность усилие, Н с учетом 5го эксперта 2.8 Учет взаимодействия показателей качества Независимость свойств по их влиянию на качество означает, что оценка влияния на качество показателя, характеризующего одно свойство, не зависит от оценки влияния на качество другого показателя, характеризующего другое свойство. В этой ситуации говорят, что взаимодействие показателей отсутствует. Существует 2 вида взаимодействия:
Взаимодействия по влиянию на качество не зависят от наличия корреляционных связей показателей. 2.8.1 Первый вид взаимодействия Способы представления взаимодействия:
Пример Пусть микроклимат в цехе завода характеризуют 2 показателя: температура и подвижность воздуха. Кривая желательности температуры воздуха, построенная одним экспертом: 10 20 30 4 2 -2 -4 0 t,˚C Кривая желательности подвижности воздуха: при t = 0˚C при t = +15˚C при t = +25˚C см/с 4 2 0 -2 -4 Данные кривые построены в предположении, что другой показатель зафиксирован на оптимальном уровне. Аналогичные графики можно построить для другой температуры или для температуры при различных значениях подвижности воздуха. Так как эти графики отличны, изменение оценок желательности по одному показателю (подвижности) зависит от значения другого показателя (температуры). Взаимодействие первого типа можно представить в виде таблицы или матрицы взаимодействия. Для каждого сочетания градации назначаются оценки желательности с помощью вспомогательной балльной шкалы. Пример: температура и подвижность. Таблица взаимодействия
Цифры без скобок – оценки желательности сочетания градаций с учетом взаимодействия показателей. Цифры в скобках – цифры, полученные простым усреднением, они не учитывают взаимодействия градаций. 2.8.2 Второй вид взаимодействия показателей качества Второй тип взаимодействия состоит в том, что в зависимости от значений, принимаемых одним показателем (или некоторой группой показателей), изменяется состав дальнейших показателей, по которым происходит оценивание качества. Алгоритм дерева свойств оказывается неприменим. В задачах, требующих учета второго типа взаимодействия, методику оценивания качества описывают с помощью специальной схемы. - схема отношений между показателями; - схема подготовки решений (СПР). СПР составляют так, чтобы, последовательно оценивая проявление указанных в ней признаков, можно было прийти к определенному решению относительно данного объекта. 2.9. Расчет комплексной оценки качества объектов Пусть построено дерево свойств объекта, определены значения показателей качества в баллах и их нормированные коэффициенты весомости. m111 m211 m212 m311 m312 m313 m314 0,30 0,20 0,13 0,37 0,63 1,0 2,5 3 1 4 3,5 балльные оценки 1-й 2-й 3-й уровни 0,37 mijk – нормированные коэффициенты весомости; i – номер уровня; j – номер группы на этом уровне; k – номер показателя в группе. Комплексная оценка качества Балльная оценка умножается на соответствующий коэффициент весомости. Полученные результаты суммируются по группам дерева свойств. K = 1*((0,37*4 + 0,30*1 + 0,20*2.5 + 0,13*3)*0,63 + 0,37*3,5) = 2,98 3 Методы оценки уровня качества продукции В соответствие с РД 50-149-79 «Методические указания по оценке технического уровня и качества промышленной продукции» при оценке качества однородной продукции следует использовать один из четырех методов:
3.1 Дифференциальный метод Дифференциальный метод заключается в сопоставлении единичных показателей качества оцениваемого изделия с соответствующими показателями базового образца (эталона). При этом определяют:
Показатели уровня качества УКi оценивают по следующим формулам: 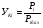 (1) (1) 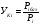 (2) где i = 1,…,n (2) где i = 1,…,nгде Pi – значение i-го показателя качества оцениваемого изделия; Piьаз – значение i-го показателя качества базового образца; n – количество единичных показателей качества. Формулу (1) используют, когда увеличению абсолютного значения показателя качества соответствует улучшение качества изделия (например: КПД, срок службы, мощность двигателя). Формулу (2) используют, если увеличение абсолютного значения показателя сопровождается ухудшением качества продукции (например: материалоемкость, содержание вредных веществ, частота отказов). По результатам расчетов делают следующие оценки:
В тех случаях, когда часть УКi≥1, а часть УКi<1 делают следующее: относительные показатели делят по значимости на 2 группы:
Если при этом оказывается, что в первой группе все УКi≥1, то можно принять, что уровень качества оцениваемого изделия не ниже уровня базового образца. Технический уровень оцениваемых изделий, для которых существенно важно значение каждого из рассматриваемых показателей, признается ниже технического уровня базового образца, если хотя бы один из относительных показателей УКi<1. В дифференциальном методе для наглядной интерпретации результатов используют диаграмму сопоставления показателей – циклограмму. Циклограмма И – изделие 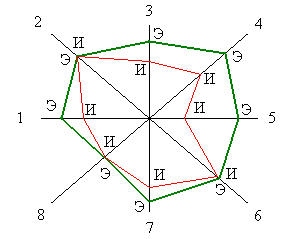 Э – эталон 1,2,…,8 – номера показателей качества Площадь многоугольника свойств изделия меньше площади многоугольника свойств эталона, следовательно, качество изделия по совокупности свойств уступает уровню качества эталона. Циклограмма позволяет наглядно увидеть, по каким показателям следует принимать управленческие решения. 3.2 Метод комплексной оценки уровня качества продукции Комплексная оценка уровня качества предусматривает использование комплексного обобщающего показателя. Комплексный показатель представляет собой функцию единичных показателей, которые характеризуют однородную группу свойств, например, технологичности, надежности. В зависимости от того, как строится комплексный показатель различают две разновидности комплексного метода:
К = f (Ki) Пример1 Показатель качества буровой установки 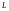 - длина проходки за срок службы (м): - длина проходки за срок службы (м):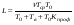
Пример 2 Главный показатель качества автобуса – Wп - годовая производительность в человеко-км. 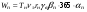 где Тн – средняя продолжительность нахождения автобуса в наряде; vэ – эксплуатационная скорость автобуса (км/ч); rн – номинальная вместимость автобуса (чел); γв – коэффициент использования вместимости автобуса; βп – коэффициент использования пробега автобуса; αп – коэффициент использования автобуса. Уровень качества продукции
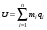 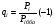
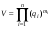 где mi - коэффициенты весомости i-го показателя; 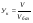 или или 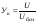 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||

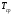 - срок службы в часах;
- срок службы в часах; 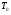 - наработка на отказ в часах;
- наработка на отказ в часах;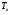 - среднее время простоя за 1 отказ (час);
- среднее время простоя за 1 отказ (час);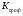 - коэффициент, характеризующий долю времени, идущего на профилактику на 1 час работы установки;
- коэффициент, характеризующий долю времени, идущего на профилактику на 1 час работы установки;  - средняя скорость бурения в м/ч.
- средняя скорость бурения в м/ч.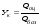
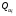 - уровень качества оцениваемой продукции;
- уровень качества оцениваемой продукции;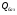 - уровень качества базового образца.
- уровень качества базового образца.