Сабақтың барысы
Сабақтың кезеңі
|
Педагогтың әрекеті
|
Оқушының әрекеті
|
Бағалау
|
Ресурстар
|
Сабақтың басы
|
Үй тапсырмасын тексеру: 1. «Ұшқыр ойдан‑ұтымды жауап»сұрақ-жауап кезеңі:
1. Төртінші дәрежелі теңдеуді шешу үшін не қолданамыз?
Жауабы: Жаңа айнымалыны енгізу арқылы.
2. Квадрат теңдеу дегеніміз не?
Жауабы: ах2+bx+c=0 түрінде берілген теңдеу квадрат теңдеу деп аталады.
3. Толымсыз квадрат теңдеу дегеніміз не?
Жауабы: b мен c нөлге тең болатын дербес жағдайлардағы квадрат теңдеу толымсыз квадрат теңдеу деп аталады.
Толымсыз квадрат теңдеулер былай жазылады:
1) ах2+bх=0 (мұндағы с=0);
2) ах2+с=0 (мұндағы b=0);
3) ах2=0 (мұндағы b=0, с=0).
4. Квадрат теңдеудің түрлерін ата?
Жауабы: Толымды квадрат теңдеу, толымсыз квадрат теңдеу, келтірілген квадрат теңдеу.
5. Толымды квадрат теңдеу дегеніміз не?
Жауабы: Егер (1) теңдеудегі b≠0 және c≠0 болса, онда ол толымды квадрат теңдеу деп аталады. Мысалы: х2-2x-1=0, 3х2-8x+5=0, 2,1х2+102,3x+0,8=0.
6. Квадрат үшмүше дегеніміз не?
Жауабы: ах2+bx+c түрінде берілген теңдеу квадрат үшмүше деп аталады.
|
Сұраққа сыни тұрғыдан ойлана отырып жауап береді.
Алдымен х2+px+q келтірілген квадрат үшмүшесін көбейткіштерге жіктейік. Бұдан былай х2+px+q=0 квадрат теңдеуінің түбірлерін х2+px+q квадрат үшмүшесінің түбірлері деп атаймыз. Бұл квадрат үшмүшенің түбірлері х2+px+q=0 теңдеуінің түбірлерімен бірдей болғандықтан, -(х1+x2)=p, х1∙x2=q теңдіктері орындалады. Сонда
х2+px+q=х2-(х1+x2)х+х1∙x2=х2-х1х+х1x2=х(х-х1)-х2(х-х1)=(х-х1)(х-х2)теңдігін аламыз. Сонымен, егер х1 және х2 сандары х2+px+q квадрат үшмүшесінің түбірлері болса, онда х2+px+q=(х-х1)(х-х2) теңдігі орындалады.
Ал жалпы жағдайда, aх2+bx+c квадрат үшмүшесінің түбірлері aх2+bx+c=0 теңдеуінің немесе  теңдеуінің түбірлерімен бірдей болады. Егер оның түбірлері х1,x2 болса, онда жоғарыдағы көрсетілгендей теңдеуінің түбірлерімен бірдей болады. Егер оның түбірлері х1,x2 болса, онда жоғарыдағы көрсетілгендей 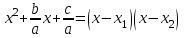 теңдігі орындалады. Сондықтан теңдігі орындалады. Сондықтан 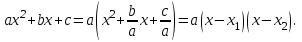 Сонымен, егер х1 және x2 сандары aх2+bx+c квадрат үшмүшесінің түбірлері болса, онда aх2+bx+c=а(х-х1)(х-х2) теңдігі орындалады. Сонымен, егер х1 және x2 сандары aх2+bx+c квадрат үшмүшесінің түбірлері болса, онда aх2+bx+c=а(х-х1)(х-х2) теңдігі орындалады.
1-мысал. х2-6x+8 квадрат үшмүшесін көбейткіштерге жіктейік. Оның түбірлері: х1=2, х2=4 болғандықтан, х2-6x+8=(х-2)(х-4) теңдігін аламыз.
2-мысал. 2х2-x-6 квадрат үшмүшесін көбейткіштерге жіктейік. Оның түбірлері: х1=-1,5;х2=2болғандықтан, 2х2-x-6=2(х-(-1,5))(х-2)=2(х+1,5)
(х-2)=(2х+3)(х-2) теңдігі орындалады.
|
Оқушылардың белсенділіген байланысты бағаланады.
|
Презентация
|
Сабақ ортасы
|
Есептер шығару:
Деңгейлік тапсырмалар:
А тобы:
. Квадрат үшмүшені көбейткіштерге жіктеуңдер: 1) х2-2x-48;
Жауабы: х1=-6;х2=8 болады, көбейткіштерге жіктеу: х2-2x-48=(х+6)(х-8).
2) х2+9x-22;
Жауабы: х1=2;х2=-11болады, көбейткіштерге жіктеу: х2+9x-22=(х-2)(х+11).
В тобы:
. Квадрат үшмүшені көбейткіштерге жіктеуңдер: 1) ах2-(а+с)x+с;
Жауабы:ах2-(а+с)x+с=ах2-аx-xс+с=ах(x-1)-c(x-1)=(ax-c)(x-1).
2) 6х2+5mx+m2;
Жауабы:6х2+5mx+m2=6х2+3mx+2mx+m2=3x(2x+m)+m(2m+m)=(3x+m)(2x+m)
|
C тобы:
Түбірлері бойынша теңдеулер құрастырып, оларды көпмүше түрінде жазыңдар. 1) -3;8;
Жауабы:
|
Оқушылардың белсенділіген байланысты бағаланады.
|
|
Сабақ соңы
|
Сөзжұмбақ шешу кезеңі.
1. Квадрат теңдеудің неше түрі бар? (үш)
2. ах2+bx+c=0 түріндегі квадрат теңдеудегі а-қандай коэффициент деп аталады? (бірінші)
3. b мен c нөлге тең болатын дербес жағдайлардағы квадрат теңдеу қалай аталады? (толымсыз)
4. Егер рационал теңдеудің екі жақ бөлігінде де бүтін өрнектер жазылса, онда оны қандай теңдеу деп атаймыз? (бүтін)
5. ах2+bx+c=0 түріндегі квадрат теңдеудегі b-қандай коэффициент деп аталады? (екінші)
6. Келтірілген квадрат теңдеудің түбірлерінің қосындысы қарама-қарсы таңбамен алынған екінші коэффициентке, ал көбейтінділері бос мүшеге тең. Бұл қай теорема? (Виет).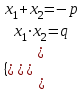
|
|
Оқушылардың белсенділіген байланысты бағаланады.
|
|
Ұзақ мерзімді жоспардың тарауы: №41
|
Күні:
|
Мектеп: Мұғалімнің аты-жөні:
|
Сынып: 8
|
Қатысқандар:
Қатыспағандар:
|
Сабақтың тақырыбы
|
Теңдеулерді шешу
|
Осы сабақта қол жеткізілетін оқу мақсаттары (оқу бағдарламасына сілтеме)
|
8.2.2.5

түріндегітеңдеулерді шешу;
8.2.2.6
бөлшек-рационал теңдеулерді шешу;
8.2.2.7
квадрат теңдеулерге келтірілетін теңдеулерді шешу;
|
Сабақтың мақсаты
|
Барлық оқушылар:
квадрат теңдеудің анықтамасымен, толымсыз квадрат теңдеулер және оларды шешу жолдарымен, келтірілген квадрат теңдеудің анықтамасымен танысады.
|
Сабақтың барысы
Сабақтың кезеңі
|
Педагогтың әрекеті
|
Оқушының әрекеті
|
Бағалау
|
Ресурстар
|
Сабақтың басы
|
Амандасу, оқушылардың зейінін сабаққа шоғырландыру;
Оқушыларды екі топқа бөлу үшін алдын ала үлестірмелі қағаздарға мына сандарды әзірлеп алып, таратамын. (4,25,36,49,100), (8,27,125,216,1000). Оқушыларды топқа бөлу: Үлестірмеде берілген сандардың қандай заңдылықпен берілгенін өздері анықтап, екі топқа бөлінеді. Топ аттары: «Бірмүше», «Дәреже».
|
Сабақтың тақырыбы мен мақсатын айқындау үшін әр топтағы оқушыларға төмендегі тапсырмаларды беремін. «Ой қозғау»
1Бөлшекті қысқарту арқылы білімдерін жинақтау.
І топ
а2 – 3а +2
а2 – 5а +6
ІІІ топ
5х2 – 9х - 2
х2 – 3х + 2
ІІ топ
в2 + 5в +6
в2 + 6в +9
№1. Үшмүшенің түбірлерін табыңдар.
1) 12х2 – 4х − 5; 12х2 – 4х − 5 = 0; D = 16 + 240 = 256 = 162
х1 = 4 – 16 = − 1/2; х2 = 4 + 16 = 5/6
24 24 х1 = − 1/2; х2 = 5/6
12х2 – 4х − 5 = 12(х + 1/2)(х – 5/6)
2) 4х2 – 64; 4х2 – 64 = 0; 4х2 = 64; х2 = 16;
х1 = − 4; х2 = 4; 4х2 – 64 = 4(х + 4)(х – 4)
№2. Квадрат үшмүшені көбейткіштерге жіктеңдер:
1) 1) х2 – 16х + 60; х2 – 16х + 60 = 0; х1 = 6; х2 = 10
х2 – 16х + 60 = (х – 6)(х – 10)
2) х2 + 20х − 96; х2 + 20х − 96 = 0; х1 = − 24; х2 = 4
х2 + 20х − 96 = (х + 24)(х – 4)0
|
Оқушылардың белсенділіген байланысты бағаланады.
|
Презентация
|
Сабақ ортасы
|
Квадрат үшмүше құрастыр
3а²-6а-4 , 5х²-4-7х , 2х²+4+х, 5х²-4-х , 2х²+4+7х,
7х2х²
Х 5х²
8,Егер түбірі белгілі болса, квадрат теңдеу құр:;
а) х 1= 1, х 2= -2.
Тексеру : а) х2+х-2 б) х2+8х+15 б) х 1= - 5, х 2= - 3. в)х1= 9 х2= -11
Жауабы : в) x2+2x -99 = 0
1) 3х²-5х-2 2)-5х²+2х-3 3) -16х²+6х+1 коэффициенттерін жазыңдар.p; деңгей. ( 2 ұпай ) Түбірлерін табыңдар: 1) х²-4х+3&2) 5х²+8х+3 3) 2х²-5х+2
|
Жауаптары :
1) х1=1, х2=3 2) х1=-3, х2=6 , 3) х1=-5, х2=2
: 1) 15(х-0,3)(х+0,4) 2) 5(х+1)(х+0,6) 3) 2(х-2)(х-0,5)
Дескриптор:
а) берілген суреттегі тіктөртбұрыштың бірінші, екінші, үшінші бөліктерінің ауданын есептейді;
б) берілген суреттегі тіктөртбұрыштың жалпы ауданын дұрыс табады.
|
Оқушылардың белсенділіген байланысты бағаланады.
|
|
Сабақ соңы
|
Оқушылар өздерінің жұмысы мен сыныптастарының жұмысын тақырып критерийлері бойынша бағалайды.
Рефлексия: Бүгінгі сабақ сіздерге ұнады ма?
Бүгінгі тақырып бойынша алған керекті ақпараттарыңызды чемоданға салыңыздар (жазыңыздар), бүгіні сабақтағы керек емес болған, артық дүниені қоқыс жәшігіне салыңыздар (жазыңыздар). Ал бүгіні ақпараттың ішінде әлі оқуым керек, толықтыруым керек дегендері болса, еттартқышқа салыңыздар (жазыңыздар)

Ең соңында оқушыларда ненің сәтті шыққандығы және әлі де нені жетілдіру керектігі жөнінде сындарлы кері байланыс беремін.
|

|
Оқушылардың белсенділіген байланысты бағаланады.
|
|
Ұзақ мерзімді жоспардың тарауы: №41
|
Күні:
|
Мектеп: Мұғалімнің аты-жөні:
|
Сынып: 8
|
Қатысқандар:
Қатыспағандар:
|
Сабақтың тақырыбы
|
Теңдеулерді шешу
|
Осы сабақта қол жеткізілетін оқу мақсаттары (оқу бағдарламасына сілтеме)
|
8.2.2.5

түріндегітеңдеулерді шешу;
8.2.2.6
бөлшек-рационал теңдеулерді шешу;
8.2.2.7
квадрат теңдеулерге келтірілетін теңдеулерді шешу;
|
Сабақтың мақсаты
|
Барлық оқушылар:
квадрат теңдеудің анықтамасымен, толымсыз квадрат теңдеулер және оларды шешу жолдарымен, келтірілген квадрат теңдеудің анықтамасымен танысады.
| |
 Скачать 2.73 Mb.
Скачать 2.73 Mb.