|
|
8сын алг 2ток. за мерзімді жоспарды тарауы Кні 09. 11
Ұзақ мерзімді жоспардың тарауы: №44
|
Күні:
|
Мектеп: Мұғалімнің аты-жөні:
|
Сынып: 8
|
Қатысқандар:
Қатыспағандар:
|
Сабақтың тақырыбы
|
Теңдеулерді шешу
|
Осы сабақта қол жеткізілетін оқу мақсаттары (оқу бағдарламасына сілтеме)
|
8.2.2.5

түріндегітеңдеулерді шешу;
8.2.2.6
бөлшек-рационал теңдеулерді шешу;
8.2.2.7
квадрат теңдеулерге келтірілетін теңдеулерді шешу;
|
Сабақтың мақсаты
|
Барлық оқушылар:
квадрат теңдеудің анықтамасымен, толымсыз квадрат теңдеулер және оларды шешу жолдарымен, келтірілген квадрат теңдеудің анықтамасымен танысады.
|
Сабақтың барысы
Сабақтың кезеңі
|
Педагогтың әрекеті
|
Оқушының әрекеті
|
Бағалау
|
Ресурстар
|
Сабақтың басы
|
Оқушыларды сапқа тұрғызып, 1-4 дейін санау арқылы топқа бөлу
Алтын ереже құру қажеттігі туралы айту.
Әр топқа бағалау парағын таратып беру.
Фигуралармен бағалау әдісімен бағалау үшін фигуралар таратып беру
«Сандарды бейнеле» ойыны
арқылы психологиялық ахуалды жақсарту
Өткен тақырықа қатысты сұрақ- жауап
Кім шапшаң әдісі бойынга
Үйге берілген тапсырманы сұрақ-жауап арқылы диалогқа түсіру
ax2+bx+c=0 а≠0
b = 0 b = 0 b ≠ 0
c = 0 c ≠ 0 c = 0
ax2 = 0 ax2 + c = 0 ax2 + bx =0
1 түбір 2 түбір 2түбір
x = 0 егер x(ax +b) = 0
-c / a> 0 x1 = 0 немесе x2 = -b / a
Түбірі жоқ
егер
-с / а < 0
x2+bx+c=0 a=1
D=b2-4ac
D>0 D=0 D<0
2 түбір 1 түбіртүбіржоқ
х=-b/2a
Виет теоремасы
x2+px+q=0
х1+х2=-p
х1*х2=q
|
Сыни ойлауға берілетін тапсырмалар, өз пікірін негіздеп, дәлелдеуді талап етеді. Әр топ оө ойын помтер арқылы қорғау керек сол арқылы жаңа тақырыпқа қадам жасайды Осы мақсатта оқушыларға қосымша өткен материалды толық меңгеру мақсатында « Ойлан тап» ойынын» пайдаландым
Мағынаны ашу:
теория  , мұндағы а , мұндағы а түрінде берілген теңдеу биквадрат теңдеу деп аталады. түрінде берілген теңдеу биквадрат теңдеу деп аталады.
Мысалы:  теңдеуін шешейік теңдеуін шешейік
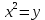
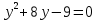
дискриминантын тауып, түбірлерін іздейміз;
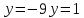
шыққан түбірді 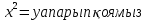 , , 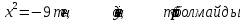
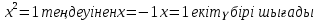
Теңдеулерді шешудің мұндай әдісі жаңа айнымалы енгізу әдісі деп аталады.
Теңдеулерді шешудің жаңа айнымалы енгізу әдісінің алгоритмін құру (оқушылармен біріге отырып)
Теңдеудегі қандайда бір өрнекті жаңа айнымалы арқылы белгілейміз
Берілген теңдеудегі өрнектің орнына жаңа айнымалыны енгізіп, жаңа айнымалыға байланысты квадрат теңдеу аламыз
Шыққан квадрат теңдеуді шешеміз
Алмастыру арқылы алғашқы айнымалының мәнін табамыз
Табылған түбірлерге тексеру жүргізіп, берілген теңдеудің түбірлерін анықтаймыз
|
Оқушылардың белсенділіген байланысты бағаланады.
|
Презентация
|
Сабақ ортасы
|
Оқушыларды сапқа тұрғызып, 1-4 дейін санау арқылы топқа бөлу
Алтын ереже құру қажеттігі туралы айту.
Әр топқа бағалау парағын таратып беру.
Фигуралармен бағалау әдісімен бағалау үшін фигуралар таратып беру
«Сандарды бейнеле» ойыны
арқылы психологиялық ахуалды жақсарту
Өткен тақырықа қатысты сұрақ- жауап
Кім шапшаң әдісі бойынга
Үйге берілген тапсырманы сұрақ-жауап арқылы диалогқа түсіру
ax2+bx+c=0 а≠0
b = 0 b = 0 b ≠ 0
c = 0 c ≠ 0 c = 0
ax2 = 0 ax2 + c = 0 ax2 + bx =0
1 түбір 2 түбір 2түбір
x = 0 егер x(ax +b) = 0
-c / a> 0 x1 = 0 немесе x2 = -b / a
Түбірі жоқ
егер
-с / а < 0
x2+bx+c=0 a=1
D=b2-4ac
D>0 D=0 D<0
2 түбір 1 түбіртүбіржоқ
х=-b/2a
Виет теоремасы
x2+px+q=0
х1+х2=-p
х1*х2=q
(Қалған оқушылар теориялық білімдерін пайдаланып кроссворд шешеді )
Егер дұрыс сөздерді тапса онда француздың математигінің фамилиясы шығады.
1. ax2+bx+c=0 а≠0 теңдеу қалай аталады? /Квадрат/
2. ax4+bx2 +c=0 а≠0 теңдеу қалай аталады? /биквадрат/
3. Квадрат теңдеуде а, b, с калай аталады ? /коэффициент /
4. Квадрат теңдеудің түбірлерінің формуласындағы түбір астындағы өрнек /дискриминант/
к в а д р а т
б и к в а д р а т
к о э ф ф и ц и е н т
д и с к р и м и н а н т
Ізденіспен Виет теоремасын пайдаланып квадрат тендеудің түбірлерін іріктеу арқылы табындар / ауызша төмендегі есептерді шығару /
1. х2 +16х + 63 = 0 / - 9 : -7 /
2. х2 +2х – 48 = 0 / - 8: 6 /
|
Формулалар галлереясы» әдісі арқылы бүгінгі тақарыбын өздері талқылап, өздері қайталау масатында қосымша тапсырмалар таратылады жаңа тақырыпқа қадам басу үшін
Формулалар галлереясы: «Ойнасаң да, ойлап тап»

Сендер квадрат теңдеу және оны шешу тәсілдерін білесіндер. Енді квадрат теңдеуге келтірілетін теңдеулерді шешу жолына тоқталайық.Ондай теңдеулердің бірі ретінде биквадрат теңдеулер қарастырылады.
Жаңа тақырып: Квадрат теңдеуге келтірілген теңдеулер
1 деңгей
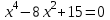
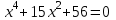
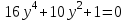
2 деңгей
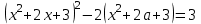
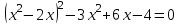
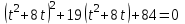
3 деңгей
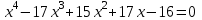
Квадрат теңдеуге келтіретін теңдеулерді жаңа айнымалы еңгізу әдісімен шешу үшін келесі алгоритмді қолданамыз:
Теңдеуге қандай да бір өрнекті жаң айнымалы арқылы белгілейміз;
Берілген теңдеудегі өрнектің орнына жаңа айнымалыны еңгізіп, жаңа айнымалыға байланысты квадрат теңдеу аламыз.
Шыққан квадрат теңдеуді шешеміз.
Алмастыру арқылы алғашқы айнымалының мәнін табамыз;
Табылған теңдеулерге тексеру жүргізіп, берілген теңдеудің түбірлерін анықтаймыз.
1-әдіс. Теңдеудің сол жақ бөлігін көбейткіштерге жіктеу
2-әдіс. Толық квадратқа келтіру әдісі
3-әдіс. Квадраттық теңдеулерді формула арқылы шешу
4-әдіс. Виет теоремасын пайдаланып теңдеулерді шешу
5-әдіс. Теңдеуді «асыра лақтыру» әдісімен шешу
6-әдіс. Квадрат теңдеулердің коэффициенттерінің қасиеттерін қолдану
7-әдіс. Квадрат теңдеуді циркуль және сызғыш көмегімен шешу
8-әдіс. Квадрат теңдеуді номограмма көмегімен шешу
9-әдіс. Квадрат теңдеулерді геометриялық әдіспен шешу
ах4 +вх2+с= 0 теңдеу қалай аталады?
Алгоритмін айт
«Кім жылдам?» интерактивті тақтадан тапсырмалар беріледі.
Оқулықпен жұмыс.
1-топ №11)х4+13х2+36=0; №190 3) х4-4х2-45=0
2-топ №2 2)х4-34х2+225=0; №190 2)х4-14х2-32=0
3-топ №3 3)х4-20х2+64=0; №190 1)х4+3х2-28=0
|
|
|
Оқушылардың белсенділіген байланысты бағаланады.
|
|
Сабақ соңы
|
Ойлан тап
Есептер шығару

Әр топ тапсырманы орындап тақтаға шығып көрсетедлі
|
Қатені тап" тақтамен жұмыс.
№
|
Тапсырмалар
|
Дұрыс жауабы
|
1
|
а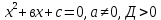
|
Теңдеудің екі түбірі бар
|
2
|
а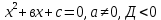
|
Теңдеудің шешімі жоқ
|
3
|
Келтірілгенквадраттеңдеудіңжалпытүрі
|
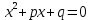
|
4
|
Квадрат теңдеудің түбірлерін табу формуласы
|
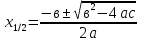
|
5
|
a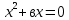 , а , а түріндегі теңдеу түріндегі теңдеу
|
Толымсы квадрат теңдеу
|
|
Оқушылардың белсенділіген байланысты бағаланады.
|
|
Ұзақ мерзімді жоспардың тарауы: №45
|
Күні:
|
Мектеп: Мұғалімнің аты-жөні:
|
Сынып: 8
|
Қатысқандар:
Қатыспағандар:
|
Сабақтың тақырыбы
|
Теңдеулерді шешу
|
Осы сабақта қол жеткізілетін оқу мақсаттары (оқу бағдарламасына сілтеме)
|
8.2.2.5

түріндегітеңдеулерді шешу;
8.2.2.6
бөлшек-рационал теңдеулерді шешу;
8.2.2.7
квадрат теңдеулерге келтірілетін теңдеулерді шешу;
|
Сабақтың мақсаты
|
Барлық оқушылар:
квадрат теңдеудің анықтамасымен, толымсыз квадрат теңдеулер және оларды шешу жолдарымен, келтірілген квадрат теңдеудің анықтамасымен танысады.
|
Сабақтың барысы
Сабақтың кезеңі
|
Педагогтың әрекеті
|
Оқушының әрекеті
|
Бағалау
|
Ресурстар
|
Сабақтың басы
|
Сұрақ-жауап кезеңі
."Білгенге маржан" берілген биквадрат теңдеулерді шешіңдер.
1.4n4-7n2+3=0;
2.x4-4x2-45=0;
3.t4-34t+225=0;
тапсырма (Интерактивті тақтада тапсырма орындалады)
1-тапсырма
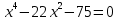 , , 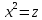
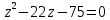 , , 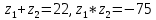 , , 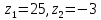
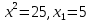 , ,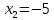 , , 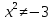
Жауабы: 5;-5
2-тапсырма
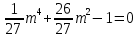 /*27 /*27
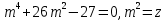
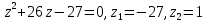
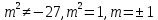
Жауабы: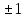
3-тапсырма
(2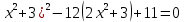 6, (2 6, (2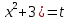
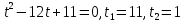
2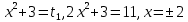
2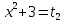 , , 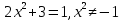
Жауабы: 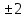
|
Есептер шығару
Тақырыпты оқып шығуға уақыт беру
Математикалық диктант
1) Теңдеуді шешіңдер: 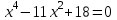
2)Түбірлері -5; 5;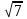 ,- ,-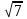 болатын биквадрат теңдеуді құрыңдар. болатын биквадрат теңдеуді құрыңдар.
3. х4-25,16х2+4=0
|
Оқушылардың белсенділіген байланысты бағаланады.
|
Презентация
|
Сабақ ортасы
|
Постермен жұмыс
1 топ Бірмүше туралы не білеміз
2 топ Көпмүше
3 топ Венн диаграммасы
Жаңа сабақты бастамас бұрын ой қозғау арқылы өткен сабаққа арналған тапсырмалар төгірегіндне жұмыс жүргізу
Ол үшір постер мен жұмыс жасату
Сен маған- мен саған
Әр топ тақырыпқа қатысты сұрақтар дайындайды
Топтарға жаңа тақырып бойынша Сен маған мен саған әдісімен конвертке салынған тапсырмалар тарату, тапсырма төңірегінде топпен жұмыс жүргізу
Берілген тапсырманы уақытылы орындау, сұрақтарға нақты жауап беру
Мына берілген өрнектерді ұқсас мүшелерді біріктіріп көпмүшенің дәрежесін анықта
5а2в-5ав2-ав-2а2в+10ав2
3а2в+5ав2-ав
Бұл көпмүшенің дәрежесі 3-ке тең
№3.
-Көбейтудің үлестірімділік заңын қолдана отырып, берілген өрнектерді теңбе-тең түрлендіргендегі алынған өрнектердің сәйкестігін тап.
Сәйкестік тест
3(2ах+5у+7) 5х2+15ху2
2а(4х+у) 6ах+15у+21
5ху(х+3у) 8ах+2ау
№4. Ұжымдық жұмыс. Проблемалық әдіс.
-Бірмүшелерді көбейту алгоритмін жаса:
-3а2в4с2*6а3в2сd=-18а5в6c3d
|
|
|
Деңгейлік есептер шығару.
№108
1) 6х*(2х-1)-7х=12х2-6х-7х=12х2-13х;
2) 2(5х-4у+1)-3(3х-3у-1) =10х-8у+2-9х+9у+3=х-8у+5;
3) а+в+с-(а-в-с) =а+в+с-а+в+с=2в+2с;
4) 7(2а+5в)-5(3в-4а) =14а+35в-15в+20а=34а+20в.
№109
(8х2+9у2+2ху-х)*(-5у) = -40х2у-45у3-10ху2+5ху
|
Оқушылардың белсенділіген байланысты бағаланады.
|
| | | |
|
|
 Скачать 2.73 Mb.
Скачать 2.73 Mb.