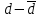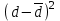Задача 1 2 Задача 2 4 Задача 3 5 Задача 1 6 Задача 2 7 Задача 3 9 Задача 1 11 Задача 2 13 Задача 1 14

• Название: Задача 1 2 Задача 2 4 Задача 3 5 Задача 1 6 Задача 2 7 Задача 3 9 Задача 1 11 Задача 2 13 Задача 1 14
• Дата: 05.09.2022
• Размер: 188.84 Kb.
• Имя файла: 30.01.21.docx
• Тип: Задача; #663366
• страница: 1 из 7

Содержание

Задача 1 2

Задача 2 4

Задача 3 5

Задача 1 6

Задача 2 7

Задача 3 9

Задача 1 11

Задача 2 13

Задача 1 14

Список использованных источников 16

Задача 1

Выявить достоверность различий (по вариативности результатов измерений) контрольной и экспериментальной группы и оценить, отличается ли система подготовки в экспериментальной группе, если при тестировании в беге на 100 м. спортсмены показали следующие результаты:

x экспер. группа	10,1	11,2	11,7	10,9	10,7	11,3	11,6	10,8	11,4	10,7
y контр. группа	11,9	12,4	12,5	12,2	13,1	11,1	10,9	11,8	12,0	12,7

Решение:

Вычислим среднее арифметическое для каждой группы в отдельности: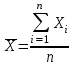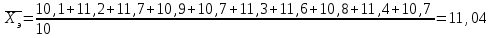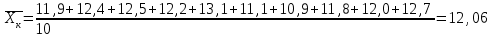







Вычислим стандартное отклонение для каждой группы: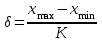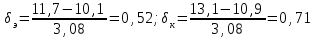





Вычислим стандартные ошибки среднего арифметического значения: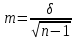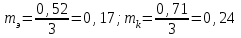





Вычислим среднюю ошибку: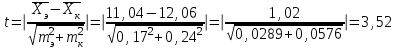



t_кр=2,08

Так как полученное в эксперименте t больше табличного значения , то различия считаются достоверными при  (при 5% уровне значимости). При достоверных различиях достаточно оснований для того, чтобы говорить о том, что методика в экспериментальной группе оказалась эффективнее методики контрольной группы.

Задача 2

Установить достоверность различий (по средним арифметическим) результатов броска мяча на дальность в двух группах школьников, занимающихся по различной методике:

1 группа	8,6	9,6	10,2	10,3	10,4	10,8	11,4	11,2	12,0	12,4
2 группа	11,0	12,2	14,2	16,4	16,4	16,5	14,9	17,1	18,4	20

Решение:

Составим вспомогательную таблицу 1.
Таблица 1 – Вспомогательная таблица

№	1 группа	2 группа	Разность (d)
1	8,6	11,0	2,4	-2,5	6,25
2	9,6	12,2	2,6	-2,3	5,29
3	10,2	14,2	4	-0,9	0,81
4	10,3	16,4	6,1	1,2	1,44
5	10,4	16,4	6	1,1	1,21
6	10,8	16,5	5,7	0,8	0,64
7	11,4	14,9	3,5	-1,4	1,96
8	11,2	17,1	5,9	1	1
9	12,0	18,4	6,4	1,5	2,25
10	12,4	18,6	6,2	1,3	1,69
Итого	106,9	155,7	48,8		22,54
среднее	10,7	15,6	4,9

Вычислим стандартное отклонение: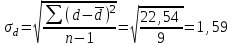



Найдем ошибку средней: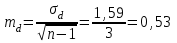



Определим t: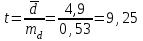



t(9;0,05)=2,262

 Полученное t больше табличного значения , то различия между первыми и вторыми измерениями считаются достоверными при  (при 5% уровне значимости). При достоверных различиях между первыми и вторыми измерениями достаточно оснований для того, чтобы говорить о том, что методика оказалась эффективной.