шпора 1. Шпора 1. 1. Статические и динамические моменты. Механическая характеристика механизма. Уре движения
 Скачать 1.35 Mb. Скачать 1.35 Mb.
|
1. Статические и динамические моменты. Механическая характеристика механизма. Ур-е движения. Классификация динамических моментов. Момент нагрузки на валу рабочей машины, или так называемый момент сопротивления движению, создается различными силами полезных и вредных сопротивлений. Полезными силами сопротивления движению являются те силы, для преодоления которых предназначена данная рабочая машина. Например, это усилия резания в металлорежущих станках, ножницах или пилах; это усилие давления металла на валки в прокатных станах; это усилия, создаваемые массой перемещаемого груза в различных подъемных механизмах. Таким образом, полезные силы сопротивления определяются конструкцией рабочей машины и особенностями технологического процесса. Вредные силы сопротивления движению обусловлены различными видами потерь, которые возникают при движении. В основном, это потери, создаваемые силами трения (в подшипниках, о воздух, трение газа в газопроводе или воды в водопроводе и т.п.). Учет величины потерь производится при помощи коэффициента полезного действия (если невозможен более точный и детальный учет), либо при помощи расчетных или эмпирических коэффициентов сопротивления движению, которые по своей сути также являются коэффициентами полезного действия, но лишь иначе записанными. И полезные и вредные силы сопротивления создают моменты статического сопротивления движению на валу рабочей машины МСМ и (при соответствующем пересчете, или так называемом приведении) на валу двигателя МС. Эти моменты сопротивления классифицируются по характеру сил сопротивления движению или по конструкции рабочей машины и особенностям технологического процесса. Механической характеристикой двигателя называется зависимость его скорости от развиваемого момента w(М) (для вращательного движения) или усилия v(F) (для поступательного движения). Различают естественную и искусственную характеристики двигателей. Естественная характеристика двигателя (она у него единственная) соответствует основной (паспортной) схеме его включения и номинальным параметрам питающего напряжения. Естественные механические характеристики двигателей вращательного движения приведены на рис. 2.5, а (1...4 - соответственно синхронного, постоянного тока с независимым возбуждением, асинхронного и постоянного тока с последовательным возбуждением). М 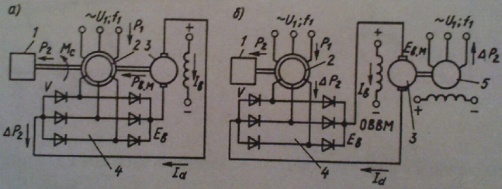 еханической характеристикой исполнительного органа называется зависимость скорости его движения от усилия или момента на нем, т. е. wио(Mио) при вращательном движении и vИO(FИO) при поступательном движении. В результате операции приведения эти характеристики преобразуются в зависимость вида w(Мс), где w - скорость двигателя, а М - приведенный к его валу момент нагрузки (сопротивления). Механические характеристики некоторых исполнительных органов приведены на рис. 2.5, б (5 - механизма главного движения металлообрабатывающего станка; 6 - транспортера, механизма подачи станка; 7 - подъемного механизма; 8 - вентилятора, дымососа, компрессора и центробежного насоса). Отметим, что реальные механические характеристики исполнительных органов более сложны по своему виду и обычно представляют собой сочетание показанных на рис. 2.5, б зависимостей. еханической характеристикой исполнительного органа называется зависимость скорости его движения от усилия или момента на нем, т. е. wио(Mио) при вращательном движении и vИO(FИO) при поступательном движении. В результате операции приведения эти характеристики преобразуются в зависимость вида w(Мс), где w - скорость двигателя, а М - приведенный к его валу момент нагрузки (сопротивления). Механические характеристики некоторых исполнительных органов приведены на рис. 2.5, б (5 - механизма главного движения металлообрабатывающего станка; 6 - транспортера, механизма подачи станка; 7 - подъемного механизма; 8 - вентилятора, дымососа, компрессора и центробежного насоса). Отметим, что реальные механические характеристики исполнительных органов более сложны по своему виду и обычно представляют собой сочетание показанных на рис. 2.5, б зависимостей.Уравнение движения электроприводов: M = MС ± Jdω/dt, Нм, где М - вращающий момент двигателя, Нм; МС - приведенный к валу двигателя момент сопротивления РМ, Нм; J - приведенный к валу двигателя момент инерции ЭП, Нм2.; ω - угловая частота вращения двигателя, рад/с. Величина Мдин = Jdω/dt называется динамическим или избыточным моментом ЭП. Положительный динамический момент обеспечивает разгон ЭП, отрицательный - замедление. Мощность двигателя Р=Мω, Вт. Поскольку ω = 2πn/60 = n/9,55 (где n измеряется в об/мин), то: Р=Мn/9550, Вт. Номинальный момент двигателя можно вычислить по приводимым в паспорте номинальной мощности РН и номинальной скорости вращения двигателя nН МН = 9550 РН/nН, Нм. Приведенный к валу двигателя момент сопротивления.MС=MРM/jŋ, Нм, где j и ŋ - соответственно передаточное отношение и КПД передачи. 2. Приведение статических моментов и моментов инерции к валу двигателя. Общие принципы решения задач приведения Ранее было показано, что для решения различных задач динамики электропривода с многоэлементной кинематической схемой необходимо составить систему уравнений движения, записанных для каждого движущегося элемента (т.е. для каждого движения привода), а также использовать уравнения связи между фазовыми координатами, учитывая постоянные передаточные числа между отдельными движущимися элементами. При этом в уравнения движения различных элементов привода войдут свои значения М, МС, J и ω или F, FС, m и v. Совместное решение уравнений движения в таком случае весьма громоздко. Та же задача может быть решена весьма просто, если реальная система двигатель-передача-рабочая машина заменяется некоторой эквивалентной системой, движущейся с одной скоростью (обычно это скорость двигателя ω или скорость рабочей машины ωМ) и для которой можно составить лишь одно уравнение движения. В это уравнение должны войти так называемые приведенные значения МС или FC, J или ω. Эквивалентная система с приведенными значениями параметров должна обладать теми же статическими и динамическими свойствами, что и реальная система. Это возможно лишь в том случае, если мощность эквивалентной системы и запас кинетической энергии ее будут теми же, что и в реальной системе. Таким образом, чтобы решить задачу приведения, надо составить уравнение баланса кинетических энергий для реальной и эквивалентной систем, а также уравнение баланса мощности для этих систем, причем при составлении уравнения баланса мощности надо обязательно иметь в виду направление потока энергии, чтобы правильно учесть потери мощности в системе. Проиллюстрируем эти общие положения на следующем примере. На рис. 3.1 показана реальная система электропривода с вращательным движением механизма, а на рис. 3.2 – эквивалентная система, приведенная к скорости двигателя. На этих рисунках: JД – момент инерции двигателя и деталей на его валу; РД - мощность на валу двигателя, вращающегося со скоростью ω; η - к.п.д. передаточного устройства; JМ – момент инерции рабочей машины, вращающейся со скоростью ωМ; РМ – мощность на валу механизма; J – приведенный момент инерции эквивалент ной системы. Параметры промежуточных валов передаточного устройства для упрощения не учтены. Рисунок 3.1 Рисунок 3.2 Уравнение баланса кинетической энергии: Уравнение баланса мощности: 1) если поток энергии идет от двигателя к механизму (т.е. если привод работает в двигательном режиме, и потери в передачах покрываются за счет мощности, забираемой двигателем из электрической сети) – 2 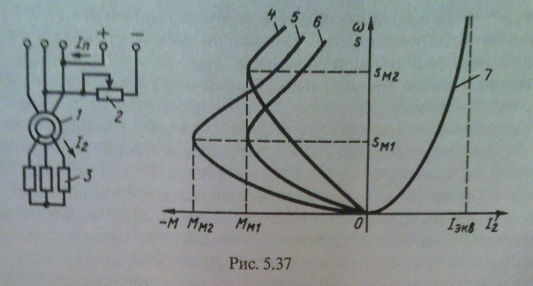 ) если поток энергии идет от механизма к двигателю (т.е. если привод работает в тормозном режиме, и потери в передачах покрываются за счет мощности, поступающей от рабочей машины) – ) если поток энергии идет от механизма к двигателю (т.е. если привод работает в тормозном режиме, и потери в передачах покрываются за счет мощности, поступающей от рабочей машины) – 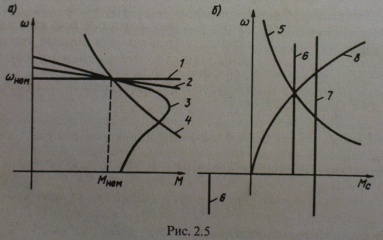 , (3.4) или , (3.4) или 3. Каскадные схемы включения асинхронных двигателей. П 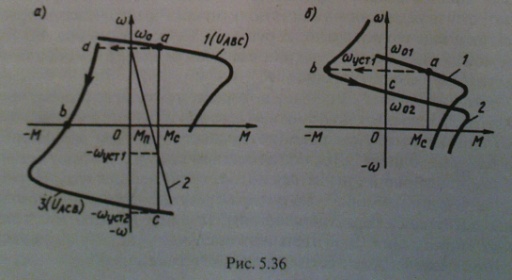 ервые схемы, в которых использовалась энергия потерь в цепи ротора, создавались путем специального соединения АД с другими электрическими машинами, поэтому эти схемы получили название каскадных. В настоящее время существуют схемы, использующие энергию скольжения АД не посредством добавочных электрических машин, а с помощью полупроводниковых приборов и трансформаторов, однако эти схемы также называют каскадными. ервые схемы, в которых использовалась энергия потерь в цепи ротора, создавались путем специального соединения АД с другими электрическими машинами, поэтому эти схемы получили название каскадных. В настоящее время существуют схемы, использующие энергию скольжения АД не посредством добавочных электрических машин, а с помощью полупроводниковых приборов и трансформаторов, однако эти схемы также называют каскадными.В общем случае каскадными называют такие схемы включения АД, которые, обеспечивая регулирование его скорости, позволяют одновременно использовать энергию потерь. По способу использования этой энергии различают схемы электромеханического и электрического машинно-вентильных каскадов. В электромеханическом машинно-вентильном каскаде (рис. 5.31, а) обмотка ротора АД 2, приводящего в движение рабочую машину 1, подключается к трехфазному неуправляемому выпрямителю 4, собранному на полупроводниковых вентилях. К выводам выпрямителя присоединен якорь вспомогательной машины постоянного тока 3, ЭДС которой Ев.м направлена навстречу ЭДС выпрямителя Ев. АД 2 и машина 3 соединены одним валом. Рассмотрим баланс мощности в этой схеме. Рис. 5.31 Поступающая из сети мощность Р1 за вычетом потерь в статоре АД 2 передается на ротор. Большая часть этой мощности, называемая электромагнитной и определяемая выражением Рэм = Mw0, в виде полезной механической мощности Р2=Мw) передается рабочей машине 1. Оставшаяся часть, определяющая мощность потерь скольжения ΔР2=Mw0S, за вычетом потерь в цепях ротора АД 2, выпрямителя 4 и вспомогательной машины 3, с помощью последней преобразуется в механическую мощность и возвращается на вал рабочей машины 1. Если пренебречь потерями в схеме, то можно установить, что рабочей машине 1 передается вся электромагнитная мощность Рэм. Действительно, на приводной вал рабочей машины от АД 2 поступает мощность Р2=Mw, а от вспомогательной машины 3 - мощность Рвм=ΔP2= Mw0S. В электрическом машинно-вентильном каскаде (см. рис. 5.31, б) в отличие от электромеханического вспомогательная машина 3 не имеет механической связи с АД 2, а соединена одним валом с синхронным генератором 5, подключенным к сети переменного тока, т. е. энергия потерь передается не на вал рабочей машины У, а отдается в сеть, рабочей же машине передается только механическая мощность Р2=Mw. 4. Переходные процессы электроприводов. Причины, обуславливающие переходные процессы. Причины возникновения переходных процессов: - изменение Мс; - изменение М, то есть переход привода с одной характеристики на другую, имеющий место при пуске, торможении, реверсе, регулировании скорости, изменении какого-либо параметра привода. Необходимость в анализе переходных процессов возникает в связи с тем, что производительность ряда ответственных механизмов (например, реверсивного прокатного стана) определяется быстротой протекания переходных процессов; качество выполнения многих технологических операций определяется переходными процессами (движение лифта, врезание резца в деталь и т.п.); механические и электрические перегрузки оборудования в большинстве случаев определяются переходными процессами. Объектом исследования, как и прежде, будет упрощенная, идеализированная модель привода - рис. 5.1. Рис. 5.1. Модель электропривода для исследования динамики Основная задача при изучении переходных процессов сводится к определению зависимостей (t), M(t) и i(t) для любых конкретных приводов в любых условиях. При изучении переходных процессов мы будем полагать известными следующие исходные данные: - начальное состояние: нач, Мнач, iнач; - конечное состояние: кон, Мкон, iкон и соответствующая ему характеристика (М); - характер изменения во времени фактора, вызвавшего переходный процесс; - параметры привода. 5. Торможение асинхронного двигателя. Т 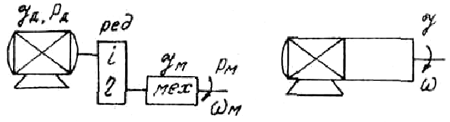 орможение противовключением осуществляется двумя путями. Один из них связан с изменением чередования на статоре двух фаз питающего АД напряжения. Допустим, например, что АД работает по механической характеристике 1 в точке а (рис. 5.36, а) при чередовании на статоре фаз напряжения сети ABC. Тогда при переключении двух фаз (например, В и С) АД переходит на работу по характеристике 3 в точкеd, участокdb которой соответствует торможению противовключением. Отметим, что при реализации торможения для ограничения тока и момента АД производится включение добавочных резисторов в цепь ротора или статора. орможение противовключением осуществляется двумя путями. Один из них связан с изменением чередования на статоре двух фаз питающего АД напряжения. Допустим, например, что АД работает по механической характеристике 1 в точке а (рис. 5.36, а) при чередовании на статоре фаз напряжения сети ABC. Тогда при переключении двух фаз (например, В и С) АД переходит на работу по характеристике 3 в точкеd, участокdb которой соответствует торможению противовключением. Отметим, что при реализации торможения для ограничения тока и момента АД производится включение добавочных резисторов в цепь ротора или статора. Другой путь перевода АД в режим торможения противовключением может быть использован при активном характере момента нагрузки Mc. Допустим, что требуется осуществить спуск груза, обеспечивая его торможение с помощью АД (так называемый тормозной спуск груза). Для этого АД включается на подъем с большим добавочным сопротивлением Ru в цепи ротора (кривая 2). Вследствие превышения моментом нагрузки Мс пускового момента двигателя М и его активного характера груз начнет опускаться с установившейся скоростью -Wуст1. АД при этом будет работать в режиме торможения противовключением. Рекуперативное торможение осуществляется в том случае, когда скорость АД превышает синхронную со0 и он работает в генераторном режиме параллельно с сетью. Такой режим возникает, например, при переходе двухскоростного АД с высокий скорости на низкую, как это показано на рис. 5.36, б. Предположим, что в исходном положении АД работал по характеристике 1 в точке я, вращаясь со скоростью w . При увеличении числа пар полюсов АД переходит на работу по характеристике 2 в точке Ь9 участок be которой соответствует торможению с рекуперацией (отдачей) энергии в сеть. Этот же вид торможения может быть реализован в системе «преобразователь частоты - двигатель» при останове АД или его переходе с характеристики на характеристику. Для этого осуществляется уменьшение частоты выходного напряжения ПЧ, а значит, и синхронной скорости w0. В силу механической инерции текущая скорость АД со будет изменяться медленнее, чем скорость вращения магнитного поля w0, т. е. будет постоянно ее превышать. За счет этого и возникает режим торможения с отдачей энергии в сеть. Отметим, что ПЧ должен быть способен при этом передать энергию от двигателя в сеть. Рекуперативное торможение является наиболее экономичным видом торможения АД. Для динамического торможения обмотку статора АД отключают от сети переменного тока и подключают к источнику постоянного тока, как это показано на рис. 5.37. Обмотка ротора АД 1 при этом может быть закорочена или в ее цепь включаются добавочные резисторы 3 с сопротивлением R Торможение при самовозбуждении основано на том, что после отключения АД от сети его электромагнитное поле затухает (исчезает не мгновенно) в течение некоторого, пусть и небольшого интервала времени. За счет энергии этого затухающего поля и использования специальных схем включения АД можно обеспечить его самовозбуждение и реализовать тормозной режим. На практике применение нашли так наливаемые конденсаторное и магн. торможение АД. 6. Переходные процессы при линейных характеристиках двигателя и механизма. Особенности расчета переходных процессов в нелинейных цепях Переходные процессы в нелинейных электрических цепях описываются нелинейными дифференциальными уравнениями, общих методов интегрирования которых не существует. На нелинейные цепи не распространяется принцип суперпозиции, поэтому основанные на нем методы, в частности классический или с использованием интеграла Дюамеля, для расчета данных цепей не применимы. Анализ переходных режимов в электрических цепях требует использования динамических характеристик нелинейных элементов, которые, в свою очередь, зависят от происходящих в них динамических процессов и, следовательно, в общем случае наперед неизвестны. Указанное изначально обусловливает в той или иной степени приближенный характер расчета переходных процессов. Переходный процесс в нелинейной цепи может характеризоваться переменной скоростью его протекания в различные интервалы времени. Поэтому понятие постоянной времени в общем случае не применимо для оценки интенсивности протекания динамического режима. Отсутствие общности подхода к интегрированию нелинейных дифференциальных уравнений обусловило наличие в математике большого числа разнообразных методов их решения, нацеленных на различные типы уравнений. Применительно к задачам электротехники все методы расчета по с 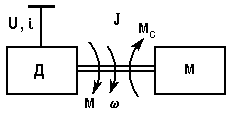 воей сущности могут быть разделены на три группы: – аналитические методы, предполагающие либо аналитическое выражение характеристик нелинейных элементов, либо их кусочно-линейную аппроксимацию; – графические методы, основными операциями в которых являются графические построения, часто сопровождаемые вспомогательными вычислительными этапами; – численные методы, основанные на замене дифференциальных уравнений алгебраическими для приращений переменных за соответствующие интервалы времени. Аналитические методы расчета Аналитическими называются методы решения, базирующиеся на аналитическом интегрировании дифференциальных уравнений, описывающих состояние нелинейной цепи с использованием аналитических выражений характеристик нелинейных элементов. Основными аналитическими методами, используемыми при решении широкого круга задач электротехники, являются: – метод условной линеаризации; – метод аналитической аппроксимации; – метод кусочно-линейной аппроксимации. 7. Пуск, регулирование скорости и торможения синхронного двигателя. О 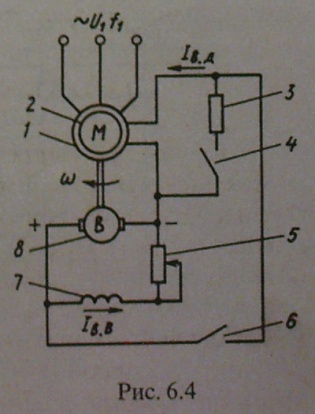 дин из способов пуска, который в настоящее время находит ограниченное применение, связан с использованием небольшого по мощности вспомогательного двигателя, устанавливаемого на валу СД. С помощью этого двигателя ротор ненатруженного СД разгоняется до синхронной скорости. после чего осуществляется его синхронизация с сетью. В системах «СД - генератор постоянного тока» в качестве вспомогательного двигателя может использоваться генератор, работающий в период пуска в двигательном режиме. дин из способов пуска, который в настоящее время находит ограниченное применение, связан с использованием небольшого по мощности вспомогательного двигателя, устанавливаемого на валу СД. С помощью этого двигателя ротор ненатруженного СД разгоняется до синхронной скорости. после чего осуществляется его синхронизация с сетью. В системах «СД - генератор постоянного тока» в качестве вспомогательного двигателя может использоваться генератор, работающий в период пуска в двигательном режиме.Н 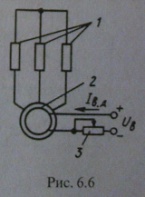 аибольшее же распространение получил другой способ пуска СД, называемый асинхронным. Для его реализации на роторе СД укладывается дополнительная пусковая обмотка, выполняемая аналогично короткозамкнутой обмотке АД типа беличьей клетки. В этом случае при подключении СД к сети переменного тока происходит его разбег аналогично АД. При под- синхронной скорости СД, отличающейся от синхронной на несколько процентов, ток подается в обмотку возбуждения двигателя и он втягивается в синхронизм с сетью. Выбор вида пусковой характеристики СД определяется конкретными условиями его работы. При пуске СД используются две основные схемы его возбуждения. аибольшее же распространение получил другой способ пуска СД, называемый асинхронным. Для его реализации на роторе СД укладывается дополнительная пусковая обмотка, выполняемая аналогично короткозамкнутой обмотке АД типа беличьей клетки. В этом случае при подключении СД к сети переменного тока происходит его разбег аналогично АД. При под- синхронной скорости СД, отличающейся от синхронной на несколько процентов, ток подается в обмотку возбуждения двигателя и он втягивается в синхронизм с сетью. Выбор вида пусковой характеристики СД определяется конкретными условиями его работы. При пуске СД используются две основные схемы его возбуждения.При использовании схемы с подключением возбудителя в конце пуска, приведенной на рис. 6.4, на первом этапе пуска контакт 6 разомкнут, а контакт 4 замкнут. Обмотка возбуждения 2 двигателя 1 оказывается замкнутой на резистор 3 и асинхронный пуск происходит в благоприятных условиях. В конце пуска при достижении подсинхронной скорости по команде специального реле управления, в качестве которого могут быть использованы реле частоты, тока или времени, контакт 4 размыкается, а контакт б замыкается. В результате в обмотку возбуждения 2 подается ток от возбудителя 8 и СД втягивается в синхронизм. Регулирование тока возбуждения осуществляется резистором 5 в цепи обмотки возбуждения 7 возбудителя. Вторая схема возбуждения СД (см. рис. 6.1, а), более простая, по- лучила название схемы с постоянно (глухо) подключенным возбудителем. В этой схеме обмотка возбуждения с самого начала пуска постоянно подключена к возбудителю 2. При скорости со 0,7(о происходит самовозбуждение возбудителя и в обмотку возбуждения СД подается ток возбуждения, благодаря чему при достижении подсинхронной скорости двигатель втягивается в синхронизм. Торможение СД, как и любого другого электродвигателя, осуществляется переводом его в генераторный режим. Наиболее часто при этом используется схема динамического торможения, приведенная на рис. 6.6 (генераторный режим при работе СД независимо от сети переменного тока). В этой схеме обмотки статора СД 2 отключаются от сети переменного тока и закорачиваются на добавочные резисторы 1 (или накоротко), а обмотка возбуждения остается подключенной к источнику возбуждения Uв через резистор 3. Торможение противовключением СД используется редко, так как перевод СД в этот режим сопровождается значительными бросками тока и момента, требует токоограничения и применения сложных схем управления. 8. Переходные процессы при нелинейных характеристиках двигателя и механизма Особенности расчета переходных процессов в нелинейных цепях П 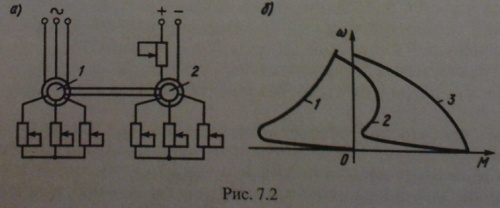 ереходные процессы в нелинейных электрических цепях описываются нелинейными дифференциальными уравнениями, общих методов интегрирования которых не существует. На нелинейные цепи не распространяется принцип суперпозиции, поэтому основанные на нем методы, в частности классический или с использованием интеграла Дюамеля, для расчета данных цепей не применимы. ереходные процессы в нелинейных электрических цепях описываются нелинейными дифференциальными уравнениями, общих методов интегрирования которых не существует. На нелинейные цепи не распространяется принцип суперпозиции, поэтому основанные на нем методы, в частности классический или с использованием интеграла Дюамеля, для расчета данных цепей не применимы.Анализ переходных режимов в электрических цепях требует использования динамических характеристик нелинейных элементов, которые, в свою очередь, зависят от происходящих в них динамических процессов и, следовательно, в общем случае наперед неизвестны. Указанное изначально обусловливает в той или иной степени приближенный характер расчета переходных процессов. Переходный процесс в нелинейной цепи может характеризоваться переменной скоростью его протекания в различные интервалы времени. Поэтому понятие постоянной времени в общем случае не применимо для оценки интенсивности протекания динамического режима. Отсутствие общности подхода к интегрированию нелинейных дифференциальных уравнений обусловило наличие в математике большого числа разнообразных методов их решения, нацеленных на различные типы уравнений. Применительно к задачам электротехники все методы расчета по своей сущности могут быть разделены на три группы: – аналитические методы, предполагающие либо аналитическое выражение характеристик нелинейных элементов, либо их кусочно-линейную аппроксимацию; – графические методы, основными операциями в которых являются графические построения, часто сопровождаемые вспомогательными вычислительными этапами; – численные методы, основанные на замене дифференциальных уравнений алгебраическими для приращений переменных за соответствующие интервалы времени. Аналитические методы расчета Аналитическими называются методы решения, базирующиеся на аналитическом интегрировании дифференциальных уравнений, описывающих состояние нелинейной цепи с использованием аналитических выражений характеристик нелинейных элементов. Основными аналитическими методами, используемыми при решении широкого круга задач электротехники, являются: – метод условной линеаризации; – метод аналитической аппроксимации; – метод кусочно-линейной аппроксимации. 9. Взаимосвязанный электропривод. Электропривод с механическим соединением валов. ВЗАИМОСВЯЗАННЫЙ ЭЛЕКТРОПРИВОД Для приведения в движение исполнительных органов ряда рабочих машин используются не один, а два или более электродвигателей, что позволяет получить некоторые специфические механические характеристики ЭП, снизить суммарный момент инерции системы по сравнению с однодвигательными приводами ЭП, создавать мощные ЭП на базе серийных двигателей относительно небольшой мощности, повысить надежность работы привода за счет резервирования, а в ряде случаев - упростить механическую часть его и рабочих машин. Е  сли два или несколько двигателей работают на общий вал (механически связаны между собой), то такой взаимосвязанный ЭП называется многодвигательным. Взаимосвязанный ЭП, обеспечивающий совместную работу двух или нескольких двигателей, валы которых не имеют непосредственной механической связи, а их взаимодействие обеспечивается электрической схемой, называется электрическим валом. сли два или несколько двигателей работают на общий вал (механически связаны между собой), то такой взаимосвязанный ЭП называется многодвигательным. Взаимосвязанный ЭП, обеспечивающий совместную работу двух или нескольких двигателей, валы которых не имеют непосредственной механической связи, а их взаимодействие обеспечивается электрической схемой, называется электрическим валом.В качестве примеров можно назвать взаимосвязанные ЭП поворотных платформ мощных экскаваторов и крупных портальных кранов, шлюзовых затворов и аэродинамической трубы. ЭЛЕКТРОПРИВОД С МЕХАНИЧЕСКИМ СОЕДИНЕНИЕМ ВАЛОВ ДВИГАТЕЛЕЙ При механическом соединении валов двигателей скорость их одинакова, а момент ЭП представляет собой алгебраическую сумму моментов отдельных двигателей. Запишем суммарный момент двух двигателей, имеющих прямолинейные характеристики: М = М1 + М2=Мк1(w01-w)/w01+Мк2(w02-w)/w02, где Мк1, Мк2, w01, w02 - соответственно моменты короткого замыкания, скорости холостого хода, w - текущая скорость. Механическая характеристика ЭП в этом случае имеет в два раза большую жесткость, а скорость его идеального холостого хода соответствует скорости холостого хода каждого двигателя. Нагрузка электродвигателей с идентичными характеристиками распределяется между ними равномерно. В большинстве случаев механические характеристики двигателей не являются идентичными и они могут иметь различные скорости идеального холостого хода или жесткости. При совместной работе таких двигателей распределение нагрузки между ними происходит неравномерно. При одинаковых скоростях идеального холостого хода, но различных жесткостях характеристик момент нагрузки Mс = M1 + M2 распределяется между двигателями так: двигатель, имеющий более жесткую характеристику, нагружается в большей степени и, наоборот, двигатель с мягкой характеристикой оказывается менее загруженным. При различных скоростях холостого хода и одинаковых жест- костях характеристик двигатели с большей скоростью холостого хода нагружаются в большей степени. М  ногодвигательный ЭП нашел достаточно широкое применение в подъемно-транспортных машинах и механизмах, так как часто бывает необходимо осуществлять их перевод на пониженную скорость перед остановкой. ногодвигательный ЭП нашел достаточно широкое применение в подъемно-транспортных машинах и механизмах, так как часто бывает необходимо осуществлять их перевод на пониженную скорость перед остановкой.В схеме ЭП с использованием двух асинхронных двигателей, приведенной на рис. 7.1, а, для понижения скорости двигатель 1 оста ется работать в двигательном режиме, а двигатель 2 переводится изменением чередования фаз в режим торможения противовключе- нием. На рис. 7.1, б приведены соответственно механические характеристики 1 и 3 этих двигателей и результирующая характеристика 2 ЭП, полученная суммированием моментов двигателей при одной и той же скорости. Участок характеристики 2 ЭП, расположенный в первом квадранте, соответствует пониженной скорости движения исполнительного органа. Отметим, что с энергетической точки зрения продолжительная работа на пониженной скорости такого ЭП является нецелесообразной, так как сопровождается большими потерями энергии в двигателе 2 (см. рис. 7.1, а). Низкая скорость двухдвигательного ЭП (рис. 7.2, а) обеспечивается при работе АД 1 в режиме двигателя, а АД 2 - в режиме динамического торможения.  10. Потери мощности и энергии в установившемся режиме работы электропривода. |
