Методы решения систем линейных алгебраических уравнений
 Скачать 151.49 Kb. Скачать 151.49 Kb.
|
|
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «КАЗАНСКИЙ (ПРИВОЛЖСКИЙ) ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ» ИНСТИТУТ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ Специальность: «Прикладная математика и информатика» Семестровая работа по курсу «Численные методы» на тему: «Методы решения систем линейных алгебраических уравнений» Работу выполнил: студент 4 курса группы 09-405 Баграмов Р.Р. Проверила: Гнеденкова В.Л. Казань 2017 год ОглавлениеПостановка задачи 2 Решение задачи 3 Реализация метода прогонки 4 Метод Якоби. 6 Метод Зейделя. 8 Метод релаксации. 10 Метод наискорейшего спуска. 13 Другие эксперименты. 16 Экспериментальная часть для метода Якоби. 16 Экспериментальная часть для метода Зейделя. 21 Экспериментальная часть для метода верхней релаксации. 26 Сравнение методов Якоби, Зейделя, верхней релаксации. 29 Листинг. 30 Постановка задачиДана система линейных уравнений, которая имеет следующий вид:  (1) (1)где 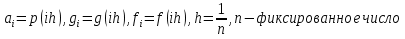 , , 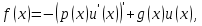 (2) (2) 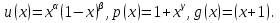 По условию задачи дано, что  следовательно: следовательно:  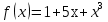 Значение функции 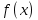 было вычислено по формуле (2). было вычислено по формуле (2).Необходимо найти решение данной системы линейных алгебраических уравнений методом прогонки, а также итерационными методами:
Решение задачиМетод прогонки. Метод прогонки для решения системы линейных уравнений в общем виде: 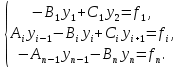 (3) (3) Решением системы (3) является вектор ( 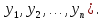 Метод прогонки заключается в том, чтобы каждый 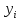 вычислить по формуле: вычислить по формуле: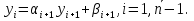 (4) (4)Формула (4) – формула прогонки. 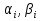 – коэффициенты прогонки. – коэффициенты прогонки. Исключая 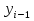 из уравнения системы с номером из уравнения системы с номером  с помощью формулы (4), получается: с помощью формулы (4), получается: Далее из предыдущего равенства выражается: 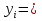 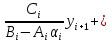 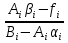 . (5) . (5)Сравнивая (4) и (5), получаются рекуррентные формулы для вычисления коэффициентов прогонки: 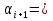 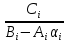 , , 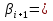 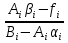 , , 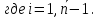 (6) (6) Выражая из первого уравнения системы (3) 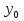 , можно найти , можно найти 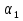 и и  : :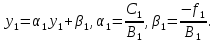 Все оставшиеся коэффициенты прогонки будут искаться по формуле (6). Далее вычисляются все 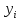 по формуле (4), где по формуле (4), где 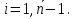 Для этого необходимо значение Для этого необходимо значение 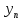 , которое получается, исключением , которое получается, исключением 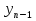 из последнего уравнения системы (3): из последнего уравнения системы (3):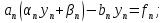  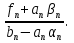 Остальные компоненты вектора ( 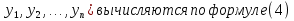 . Такое вычисление называется обратным ходом метода прогонки. . Такое вычисление называется обратным ходом метода прогонки.Метод прогонки справедлив только для систем уравнений с трёхдиагональной матрицей. Необходимо убедиться, что исходная система уравнений имеет матрицу c диагональным преобладанием. Действительно, матрица коэффициентов системы (1) в нашем случае имеет вид: 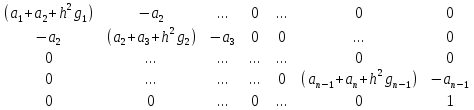 |
