Задачи по теории надежности. Практическое 3анятие 1 Определение количественных характеристик надежности по статистическим данным об отказах изделия. Теоретические сведения
 Скачать 1.43 Mb. Скачать 1.43 Mb.
|
|
Введение Настоящее пособие посвящено теории и практике решения задач по дисциплине «Надежность технических систем и техногенный риск» для закрепления теоретических знаний и практики использования основных методов расчета и оценки критериев надежности сложных технических систем. Для облегчения решения задач в пособии приведены основные сведения из теории, расчетные формулы, а так же типовые примеры с решениями. Основная цель данного пособия – формирование навыков практического применения теории надежности к решению различных практических задач. Пособие рассчитано на широкий круг инженеров, студентов и аспирантов занимающихся созданием и эксплуатацией сложных технических систем. Пособие преследует учебные цели, поэтому все задачи носят гипотетический характер ПРАКТИЧЕСКОЕ 3АНЯТИЕ № 1 Определение количественных характеристик надежности по статистическим данным об отказах изделия. Теоретические сведения Вероятность безотказной работы по статистическим данным об отказах оценивается выражением
где n(t) - число изделий, не отказавших к моменту времени t; N- число изделий, поставленных на испытания; Р*(t) - статистическая оценка вероятности безотказной работы изделия. Для вероятности отказа по статистическим данным справедливо соотношение
где N-n(t)- число изделий, отказавших к моменту времени t; q*(t) - статистическая оценка вероятности отказа изделия. Частота отказов по статистическим данным об отказах определяется выражением
где n(t) - число отказавших изделий на участке времени (t, t+t); f*(t) - статистическая оценка частоты отказов изделия; t - интервал врeмени. Интенсивность отказов по статистическим данным об отказах определяется формулой
где n(t)- число изделий, не отказавших к моменту времени t; n(t) - число отказавших изделий на участке времени (t, t+t) ; *(t)- статистическая оценка интенсивности отказов изделия. Среднее время безотказной работы изделия по статистическим данным оценивается выражением
где ti - время безотказной работы i- го изделия; N- общее число изделий, поставленных на испытания; mt* - статистическая оценка среднего времени безотказной работы изделия. Для определения mt* по формуле (1.5) необходимо знать моменты выхода из строя всех N изделий. Можно определять mt* из уравнения
где ni - количество вышедших из строя изделий в i- ом интервале времени; tср.i = (ti-1+ti)/2 ; m=tk/t ; t=ti+1-ti ; ti-1 -время начала i- го интервала; ti- время конца i- го интервала; tk - время, в течение которого вышли из строя все изделия; t-интервал времени. Дисперсия времени безотказной работы иэделия по статистическим данным определяется формулой
где Dt*- статистическая оценка дисперсии времени безотказной работы изделия. Решение типовых задач Задача 1.1. На испытание поставлено 1000 однотипных электронных ламп, за 3000 час. отказало 80 ламп. Требуется определить P*(t), q*(t) при t = 3000 час. Решeниe. В данном случае N= 1000; n(t)=1000-80=920; N-n(t)=1000-920=80. По формулам (1.1) и (1. 2) определяем или 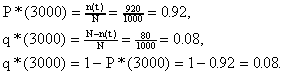 Задача 1.2. На испытание было поставлено 1000 однотипных ламп. За первые 3000 час. отказало 80 ламп, а за интервал времени 3000 - 4000 час. отказало еще 50 ламп. Требуется определить статистическую оценку частоты и интенсивности отказов элвктронных ламп в промежутке времени 3000 - 4000 час. Решение. В данном случае N=1000; t=3000 час; t =1000 час; n(t)=50; n(t)=920. По формулам (1.3) и (1.4) находим Задача 1.3. На испытание поставлено N = 400 изделий. За время t = 3000 час отказало 200 изделий, т.е. n(t) = 400-200=200.За интервал времени (t, t+t) , где t= 100 час, отказало 100 изделий, т.е. n(t)= 100. Требуется определить Р*(3000), P*(3100), f*(3000), *(3000). Решение. По формуле (1.1) находим 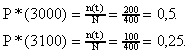 Используя формулы (1.3) и (1.4), получим Задача1.4. На испытание поставлено 6 однотипных изделий. Получены следующие значения ti (ti - время 6езотказной работы i- го изделия) : t1 =280 час; t2 = 350 час; t3 =400 час; t4 =320 час; t5 =380 час; t6 =330 час. Определить статистическую оценку среднего времени безотказной работы изделия. Решение. По формуле (1.5) имеем Задача 1.5. За наблюдаемый период эксплуатации в аппаратуре было зафиксировано 7 отказов. Время восстановления составило: t1 =12мин.; t2=23мин.; t3 =15мин.; t4=9мин.; t5=17мин.; t6=28мин.; t7=25мин.; t8=31мин. Требуется определить среднее время восстановления аппаратуры Решение. Задача 1.6. В результате наблюдения за 45 образцами радиоэлектронного оборудования получены данные до первого отказа всех 45 образцов, сведенные в табл.1.1. Требуется определить mе*. Таблица 1.1
Решение. В данном случае  Используя формулу (1.6), получим Задачи для самостоятельного решения Задача 1.7. На испытание поставлено 100 однотипных изделий. За 4000 час. отказало 50 изделий. За интервал времени 4000 - 4100 час. отказало ещё 20 изделий. Требуется определить f*(t),*(t) при t=4000 час. Задача 1.8. На испытание поставлено 100 однотипных изделий. За 4000 час. отказало 50 изделий. Требуется определить p*(t) и q*(t) при t=4000 час. Задача 1.9. В течение 1000 час из 10 гироскопов отказало 2. За интервал времени 1000 - 1100 час. отказал еще один гироскоп. Требуется определить f*(t), *(t) при t =1000 час. Задача 1.10. На испытание поставлено 1000 однотипных электронных ламп. За первые 3000 час. отказало 80 ламп. За интервал времени 3000 - 4000 час. отказало еще 50 ламп. Требуется определить p*(t) и q*(t) при t=4000 час. Задача 1.11. На испытание поставлено 1000 изделий. За время t=1300 час. вышло из строя 288 штук изделий. За последующий интервал времени 1300-1400 час. вышло из строя еще 13 изделий. Необходимо вычислить p*(t) при t=1300час. и t=1400 час.; f*(t), *(t) при t =1300 час. Задача 1.12. На испытание поставлено 45 изделий. За время t=60 час. вышло из строя 35 штук изделий. За последующий интервал времени 60-65 час. вышло из строя еще 3 изделия. Необходимо вычислить p*(t) при t=60час. и t=65 час.; f*(t), *(t) при t =60 час. Задача 1.13. В результате наблюдения за 45 образцами радиоэлектронного оборудования, которые прошли предварительную 80-часовую приработку, получены данные до первого отказа всех 45 образцов, сведенные в табл.1.2. Необходимо определить mt*. Таблица 1.2.
Задача 1.14. На испытание поставлено 8 однотипных изделий. Получены следующие значения ti (ti - время безотказной работы i-го изделия): t1 =560час.; t2=700час.; t3 =800час.; t4=650час.; t5=580час.; t6=760час.; t7=920час.; t8=850час. Определить статистическую оценку среднего времени безотказной работы изделия. Задача1.15. За наблюдаемый период эксплуатации в аппаратуре было зарегистрировано 6 отказов. Время восстановления составило: t1 =15мин.; t2=20мин.; t3 =10мин.; t4=28мин.; t5=22мин.; t6=30мин. Требуется определить среднее время восстановления аппаратуры Задача1.16. На испытание поставлено 1000 изделий. За время t=11000 час. вышло из строя 410 изделий. Зв последующий интервал времени 11000-12000 час. вышло из строя еще 40 изделий. Необходимо вычислить p*(t) при t=11000 час. и t=12000 час., а также f*(t), *(t) при t=11000 час. ПРАКТИЧЕСКОЕ 3АНЯТИЕ № 2 Аналитическое определение количественных характеристик надёжности изделия. Теоретические сведения В 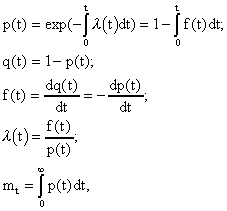 ыпишем формулы, по которым определяются количественные характеристики надежности изделия ыпишем формулы, по которым определяются количественные характеристики надежности изделия (2.1) (2.2) (2.3) (2.4) (2.5) где p(t) - вероятность безотказной работы изделия на интервале времени от 0 до t; q(t) - вероятность отказа изделия на интервале времени от 0 до t; f(t)-частота отказов изделия или плотность вероятности времени безотказной работы изделия Т; (t)- интенcивность отказов изделия; mt - среднее время безотказной работы изделия. Формулы (2.1) - (2.5) для экспоненциального закона распределения времени безотказной работы изделия примут вид
Формулы (2.1) - (2.5) для нормального закона распределения времени безотказной работы изделия примут вид
где Ф(U) - функция Лапласа, обладающая свойствами Ф(0)=0 ; (2. 15) Ф(-U) =-Ф(U) ; (2.16) Ф()=0.5 . (2.17) Значения функции Лапласа приведены в приложении П.7.13 [ 1 ] . Значения функции (U) приведены в приложении П.7.17 [ 1 ]. Здесь mt - среднее значение случайной величины Т; t2 - дисперсия случайной величины Т; Т- время безотказной работы изделия. Формуды (2.1) - (2.5) для закона распределения Вейбулла времени безотказной работы изделия имеют вид
где a, k - параметры закона распределения Вейбулла. Г (x) - гамма-функция, значения которой приведены в приложении П.7.18 [ 1 ]. Формулы (2.1) - (2.5) для закона распределвния Релея времени безотказной работы изделия имеют вид
где t – мода распределения случайной величины Т; Т – время безотказной работы изделия. Решение типовых задач Задача 2.1. Время работы элемента до отказа подчинено экспоненциальному закону распределения с параметром =2.510-5 1/час. Требуется вычислить количественные характеристики надежности элемента p(t),q(t),f(t),mt для t=1000час. Решение. Используем формулы (2.6), (2.7), (2.8), (2.10) для p(t),q(t),f(t),mt . 1. Вычислим вероятность безотказной работы: Используя данные таблицы П.7.14 [ 1 ] получим 2. Вычислим вероятность отказа q(1000). Имеем q(1000)=1-p(1000)=0.0247 . 3. Вычислим частоту отказов 4. Вычислим среднее время безотказной работы Задача 2. 2. Время работы элемента до отказа подчинено нормальному закону с параметрами mt =8000 час, t =2000 час. Требуется вычислить количественные характеристики надежности p(t),f(t),(t),mt для t=10000 час. Решение. Воспользуемся формулами (2.11), (2.12), (2.13),(2.14) для p(t), f(t), (t),mt. 1. Вычислим вероятность безотказной работы p(t)=0.5Ф(U) ; U=(t-mt)/t ; U=(10000-8000)/2000=1; Ф(1)=0.3413 ; p(10000)=0.5-0.3413=0.1587. 2. Определим частоту отказа f(t)  . . Введем обозначение 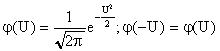 . . Тогда f(t)=(U)/t ; U=(t-mt)/t f(1000)=(1)/2000=0.242/2000=12.110-5 1/час. 3. Рассчитаем интенсивность отказов (t) (t)=f(t)/p(t); (10000)=f(10000)/p(10000)=12.110-5 /0.1587=76.410-5 1/час. 4. Среднее время безотказной работы элемента mt = 8000 час. Задача 2.3. Время работы изделия до отказа подчиняется закону распределения Релея. Требуется вычислить количественные характеристики надежности изделия p(t),f(t),(t),mt для t=1000час ,если параметр распределения t=1000 час. Решение. Воспользуемся формулами (2.23), (2.25), (2.27),(2.26) для p(t),f(t), mt ,(t). 1. Вычислим вероятность безотказной работы p(t) 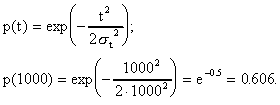 2. Определим частоту отказа f(t) f(t)=tp(t)/t2 ; f(1000)=10000.606/10002=0.60610-3 1/час. 3. Рассчитаем интенсивность отказов (t)= t/t 2 ; (1000)=1000/10002 =10-3 1/час. 4. Определим среднее время безотказной работы изделия Задача 2.4. Время безотказной работы изделия подчиняется закону Вейбулла с параметрами k=1.5; a=10-4 1/час, а время работы изделия t=100 час. Требуется вычислить количественные характеристики надежности изделия p(t),f(t),(t),mt . Решение. 1. Определим вероятность безотказной работы p(t) по формуле (2.18) . Имеем p(t)=exp(-atk ); p(100)=exp(-10-4 1001.5 ); x=1001.5 ; lg x=1,5lg 100=3; x=1000; p(100)=e-0,1 =0,9048. 2. Определим частоту отказов f(t) f(t)=aktk-1 p(t); f(100)=10-4 1,51000,5 0,90481,3510-3 1/час. 3. Определим интенсивность отказов (t) (t)=f(t)/p(t) ; (100)=f(100)/p(100)=1,3510-3 /0.90481,510-3 1/час. 4. Определим среднее время безотказной работы изделия mt  . . Так как zГ(z)=Г(z+1), то x=10-2,666 ;lg x=-2,666lg10=-2,666= Используя приложение П.7.18 [1], получим m t =0,90167/0,00215=426 час. Задача 2.5. В результате анализа данных об отказах аппаратуры частота отказов получена в виде Требуется определить количественные характеристики надежности: p(t), (t),mt. Решение. 1. Определим вероятность безотказной работы. На основании формулы (2.1) имеем 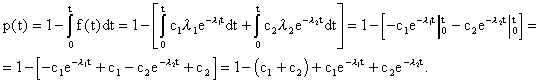 Вычислим сумму С1+ С2 Так как 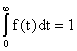 , то , то 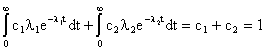 . .Тогда 2. Найдем зависимость интенсивности отказов от времени по формуле  . . 3. Определим среднее время безотказной работы аппаратуры. На основании формулы (2.5) будем иметь 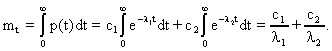 Задачи для самостоятельного решения Задача 2.6.Вероятность безотказной работы автоматической линии изготовления цилиндров автомобильного двигателя в течении 120 час равна 0.9. Предполагается, что справедлив экспоненциальный закон надежности. Требуется рассчитать интенсивность отказов и частоту отказов линии для момента времени t =120 час., а также среднее время безотказной работы. Задача 2.7. Среднее время безотказной работы автоматической системы управления равно 640 час. Предполагается, что справедлив экспоненциальный закон надежности. Необходимо определить вероятность безотказной работы в течение 120 час., частоту отказов для момента времени t=120 час и интенсивность отказов. Задача 2.8. Время работы изделия подчинено нормальному закону с параметрами mt = 8000 час., t =1000 час. Требуется вычислить количественные характеристики надежности p(t) , f(t) , (t) , mt для t=8000 час. Задача 2.9.Время безотказной работы прибора подчинено закону Релея с параметром t= 1860 час. Требуется вычислить Р(t), f(t),(t) для t = 1000 час и среднее время безотказной работы прибора. Задача 2.10. Время исправной работы скоростных шарикоподшипников подчинено закону Вейбулла с параметрами к=2,6 ; а= 1,65*10-7 1/час. Требуется вычислить количественные характеристики надежности Р(t), f(t), (t) для t=150 час. и среднее время безотказной работы шарикоподшипников. Задача 2.11.Вероятность безотказной работы изделия в течение t=1000 час. Р(1000)=0,95. Время исправной работы подчинено закону Релея. Требуется определить количественные характеристики надежности f(t), (t), mt. Задача 2.12. Среднее время исправной работы изделия равно 1260 час. Время исправной работы подчинено закону Релея. Необходимо найти его количественные характеристики надежности P(t), f(t), (t) для t=1000 час. Задача 2.13. В результате анализа данных об отказах изделия установлено, что частота отказов имеет вид f(t)=2e-t (1-e-t ) . Необходимо найти количественные характеристики надежности P(t), (t), mt. Задача 2.14. В результате анализа данных об отказах изделий установлено, что вероятность безотказной работы выражается формулой P(t)=3e-t-3e-2t+e-3t. Требуется найти количественные характеристики надежности P(t), (t), mt. Задача 2.15. Определить вероятность безотказной работы и интенсивность отказов прибора при t = 1300 часов работы, если при испытаниях получено значение среднего времени безотказной работы mt=1500 час. и среднее квадратическое отклонение t= 100 час. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3 Последовательное соединение элементов в систему. Теоретические сведения Соединение элементов называется последовательным, если отказ хотя бы одного элемента приводит к отказу всей системы. Система последовательно соединенных элементов работоспособна тогда, когда работоспособны все ее элементы. Вероятность безотказной работы системы за время t определяется формулой Pc(t) =P1(t)*P2(t)...Pn(t)= (3.1) где Рi(t) - вероятность безотказной работы i-го элемента за время t. Если Рi (t) =Р(t), то Pc(t)=Pn(t). (3.2) Выразим Рс(t) через интенсивность отказов i(t) элементов системы. Имеем: 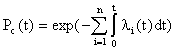 (3. 3) (3. 3)или 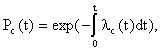 (3.4) (3.4)где Здесь i(t) – интенсивность отказов i-го элемента; с(t) – интенсивность отказов системы. Вероятность отказа системы на интервале времени (0, t ) равна Частота отказов системы fc(t) определяется соотношением Интенсивность отказов системы Среднее время безотказной работы системы:  (3. 9) (3. 9) В случае экспоненциального закона надежности всех элементов системы имеем 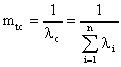 ; (3.16) ; (3.16) где mti - среднее время безотказной работы i - го элемента. При расчете надежности систем часто приходится перемножать вероятности безотказной работы отдельных элементов расчета, возводить их в степень и извлекать корни. При значениях Р(t), близких к единице, эти вычисления можно с достаточной для практики точностью выполнять по следующим приближенным формулам: 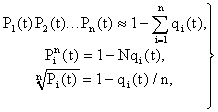 (3.18) (3.18) где qi (t) – вероятность отказа i - го элемента. Решение типовых задач Задача 3.1. Система состоит из трех устройств. Интенсивность отказов электронного устройства равна i=0,16*10-3 1/час = const. Интенсивности отказов двух электромеханических устройств линейно зависят от времени и определяются следующими формулами λ2=0,23*10-4t 1/час, λ 3=0,06*10-6t2,6 1/час. Необходимо рассчитать вероятность безотказной работы изделия в течение 100 час. Решение. На основании формулы (3.3) имеем 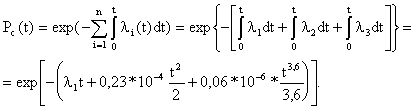 Для t=100 час  . .Задача 3.2. Система состоит из трех блоков, среднее время безотказной работы которых равно : mt1=160 час; mt2 =320 час; mt3 = 600 час. Для блоков справедлив экспоненциальный закон надежности. Требуется определить среднее время безотказной работы системы. Решение. Воспользовавшись формулой (3.17) получим Здесь i - интенсивность отказов i -го блока. На основании формулы (3.11) имеем Здесь λc – интенсивность отказов системы. На основании формулы (3.16) получим: Задача 3.3. Система состоит из 12600 элементов, средняя интенсивность отказов которых ср=0,32*10-6 1/час. Требуется определить Pc(t), qc(t), fc(t), mtc, для t=50 час. Здесь Pc(t) - вероятность безотказной работы системы в течение времени t; qc(t) - вероятность отказа системы в течение времени t ; fc(t) - частота отказов или плотность вероятности времени T безотказной работы системы; mtс - среднее время безотказной работы системы. Решение. Интенсивность отказов системы по формуле (3.11) будет с = ср*n = 0,32*10-6*12600 = 4,032*10-3 1/час . Из (3.13) имеем Рс(t) = e-ct ; Рс(50) = e-4,032*0,001*50 0,82 . Из (3.15) получим qc(t)= 1- Pc(t) = cPc(t); qc(50)=1-Pc(50) 0,18 . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

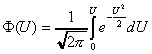 ;
;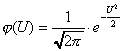
 ,
,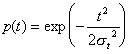 ;
;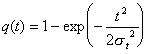 ;
;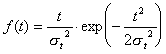 ;
;