Поурочные+планы+по+геометрии+2+часть. Урок 25 аксиома параллельных прямых цели дать представление об аксиомах геометрии ввести аксиому параллельных прямых и следствия из нее. Ход урока
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
8f Урок 25 АКСИОМА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ Цели: дать представление об аксиомах геометрии; ввести аксиому параллельных прямых и следствия из нее. Ход урока I. Анализ результатов самостоятельной работы. II. Изучение нового материала. 1. Беседа об аксиомах геометрии. 2. Записать в тетрадях: аксиомами называются те основные положения геометрии, которые принимаются в качестве исходных положений, на основе которых доказываются далее теоремы и строится вся геометрия. 3.Задача: через точку М, не лежащую на прямой а, провести прямую, параллельную прямой а. Решение этой задачи доказывает существование прямой, проходящей через данную точку и параллельной данной прямой. 4. Вопрос к учащимся: сколько таких прямых можно провести? 5. В геометрии Евклида, изложенной им в книге «Начала» ответ на данный вопрос следует из знаменитого пятого постулата, и этот ответ таков: через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. Пятый постулат знаменит тем, что долгие годы его пытались доказать на основе остальных аксиом Евклида. И лишь в прошлом веке, во многом благодаря великому русскому математику Н. И. Лобачевскому, было доказано, что пятый постулат не может быть выведен из остальных аксиом. Поэтому утверждение о единственности прямой, проходящей через данную точку параллельно данной прямой, принимается в качестве аксиомы. 6. В аксиоме утверждается, что через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной (единственность прямой), а существование такой прямой доказывается. III. Закрепление изученного материала. 1. Устно решить задачи №№ 196, 197. Указание: при решении задачи № 197 показать два возможных случая расположения прямых: 1) все четыре прямые пересекают прямую р; 2) одна из четырех прямых параллельна прямой р, а три другие прямые пересекают ее. Эти два случая иллюстрируют ответ на вопрос задачи: по крайней мере, три прямые пересекают прямую р. 2. Разъяснение смысла понятия «следствия». Записать в тетрадях: следствиями называются утверждения, которые выводятся непосредственно из аксиом или теорем. 3. Рассмотреть следствия 1° и 2° из аксиомы параллельных прямых. 4. Решить задачи №№ 198, 200, 218. Решение задачи № 218: отметим произвольную точку, не лежащую на прямой b, и проведем через нее прямую с, параллельную прямой b. Так как прямая а пересекает прямую b, то она пересекает и прямую с. Таким образом, прямая с пересекает прямую а и параллельна прямой b. 5. Решить задачу № 219*. Решение Предположим, что прямые а и b не параллельны, то есть пересекаются. Тогда можно провести прямую с, которая пересекает прямую а и не пересекает прямую b (задача № 218). Но это противоречит условию задачи. Значит, наше предположение неверно и а || b. IV. Итоги урока. Домашнее задание: изучить пункты 27 и 28; ответить на вопросы 7–11 на с. 68 учебника; решить задачи №№ 217, 199. Урок 26 СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ Цели: рассмотреть свойства параллельных прямых; добиться от учащихся понимания того, что накрест лежащие, соответственные и односторонние углы можно рассмотреть для любых двух прямых и секущей, но только в случае параллельных прямых накрест лежащие углы равны, соответственные углы равны, а сумма односторонних углов составляет 180°. Ход урока I. Проверка усвоения материала учащимися. 1. Сформулировать определение параллельных прямых. 2. Повторить признаки параллельности двух прямых. 3. Сформулировать аксиому параллельных прямых. 4. Повторить следствия из аксиомы параллельных прямых. 5. Устно решить задачу: докажите, что прямая, параллельная основанию АС равнобедренного треугольника АВС, перпендикулярна прямой ВD, где ВD – медиана треугольника. II. Объяснение нового материала. 1. Во всякой теореме различают две части: условие и заключение. Условие теоремы – это то, что дано, а заключение – то, что требуется доказать. 2. Привести примеры изученных теорем и выделить в них условие и заключение (это делают учащиеся). 3. Ввести понятие теоремы, обратной данной. 4. Сформулировать теоремы, обратные трём теоремам п. 25, выражающим признаки параллельности прямых. Необходимо сравнить условия и заключения двух теорем: теоремы, выражающей признак параллельности двух прямых, и обратной, составив следующую таблицу:
5. Рассмотреть доказательство теоремы о накрест лежащих углах по рисунку 113 и таблице. 6. Акцентировать внимание учащихся на методе доказательства от противного, с помощью которого и была доказана теорема. Кроме того, важно отметить, что если верно некоторое утверждение, то отсюда еще не следует, что и обратное утверждение тоже верно. Например, рассмотрим два утверждения: 1) Если точка С – середина отрезка АВ, то АС = ВС. 2) Если АС = ВС, то точка С – середина отрезка АВ. Второе утверждение является обратным первому. Первое утверждение верно, в то время как второе неверно. В самом деле, в равнобедренном треугольнике АВС с основанием АВ отрезки АС и ВС равны, но точка С не является серединой отрезка АВ. 7. Самостоятельно по учебнику учащиеся изучают теоремы о свойствах соответственных и односторонних углов, образованных двумя параллельными и секущей. III. Закрепление изученного материала. 1. Устно по рисунку 114 учебника доказать следствие: если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой. 2. Устно решить №№ 201, 205 по рисунку 117 и № 209 по рисунку 118. IV. Итоги урока. Домашнее задание: изучить п. 29; повторить пункты 15–28; ответить на вопросы 1–15 на с. 68 учебника; решить задачи №№ 202 и 212. Урок 27 СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ. Цели: закрепить знание свойств параллельных прямых в ходе выполнения упражнений и решения задач; систематизировать знания учащихся; развивать логическое мышление учащихся. Ход урока I. Проверочная работа (10 мин). Вариант I 1. Сформулируйте аксиому параллельных прямых. 2. Какая теорема называется обратной данной теореме? Приведите примеры теорем, обратных данным. 3. Докажите, что при пересечении двух параллельных прямых секущей соответственные углы равны. Вариант II 1. Объясните, какие утверждения называются аксиомами. Приведите примеры аксиом. 2. Дайте определение параллельных прямых. Какие два отрезка называются параллельными? 3. Докажите, что при пересечении двух параллельных прямых секущей сумма односторонних углов равна 180°. II. Выполнение упражнений. 1. По готовому на доске чертежу рисунка 1 решить задачи:  Рис. 1 1) Дано: а || b, с – секущая; 2) Дано: а || b, с – секущая; 3) Дано: а || b, с – секущая; 4) Дано: а || b, с – секущая; 2. На доске и в тетрадях решить задачи №№ 203 (б), 211 (в). Решение задачи № 211 (в)
Значит, 3. Устно по готовому чертежу на доске (см. рис. 3) решить № 220. Решение Пусть при пересечении двух прямых а и b секущей накрест лежащие углы 1 и 2 не равны: 4. Решить задачу № 221. Решение
Итак, через точку А можно провести только одну прямую, параллельную ВС. Следовательно, прямые АМ и AN совпадают, то есть точки M, А и N лежат на одной прямой. III. Итоги урока. Домашнее задание: повторить изученный материал пунктов 24–29; ответить на вопросы 1–15 на с. 68 учебника; подготовиться к устному опросу; решить задачи №№ 203(а), 208, 211(а). Урок 28 РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ «ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ» Цели: привести в систему знания учащихся по данной теме, добиться четкого понимания того, когда в задаче нужно применить признак параллельности двух прямых, а когда – свойство параллельных прямых. Ход урока I. Устный опрос учащихся по карточкам. Вариант I 1. Сформулируйте один из признаков параллельности двух прямых. 2. Докажите, что прямые а и b, изображенные на рисунке 1, параллельны, если 3. На рисунке 2 прямые АD и ВK параллельны, луч ВD – биссектриса угла АВK, Вариант II 1. Сформулируйте аксиому параллельных прямых. 2. Дан треугольник СDЕ. Сколько прямых, параллельных стороне СЕ, можно провести через вершину D? 3. На рисунке 3 отрезки АВ и СD пересекаются в их общей середине М. Через точку В проведена прямая а, параллельная прямой АD. Докажите, что прямая а проходит через точку С. Вариант III 1. Сформулируйте одно из свойств параллельных прямых. 2. На рисунке 4 прямые а и b параллельны; 3. На рисунке 5 АВ = ВС; ВF || АС. Докажите, что луч ВF – биссектриса угла СВD. 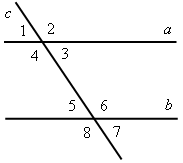 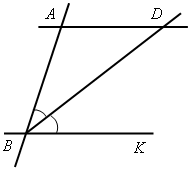 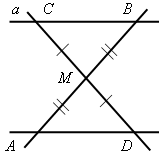 Рис. 1 Рис. 2 Рис. 3   Рис. 4 Рис. 5 |




