шпоры фх. 1. Физическая химия цель, задачи, методы исследования. Основные понятия физической химии. Физ химия
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
|
Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией. Для многих систем единственный вид работы – работа расширения. Практическое значение имеет обычно работа расширения газа причем многие газы при достаточно низких давлениях и сравнительно высоких температурах приближенно подчиняется законам идеальных газов. Рассмотрим математические соотношения для вычисления работы расширения идеального газа в различных процессах. При расширении газа совершается работа, которая вычисляется по уравнению: 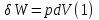 Или в интегральной форме 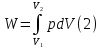 Вычисление по формуле(2) работа представляет собой максимальную работу, которую совершает газ при протекании процесса в условиях, близких к равновесным (обратимый процесс). При протекании процесса в условиях, далеких от равновесного (необратимый процесс), совершаемая газом работа меньше, чем вычисленная по этой формуле. Для интегрирования уравнения (2) нужно знать зависимость между давлением и объемом газа, т.е. уравнение состояния газа . Эта зависимость для идеального газа описывается уравнением состояния Клайперона – Менделеева: pV=nRT (3). Где n – количество идеального газа в молях; R – универсальная газовая постоянная, равная 8,314 Дж/моль*К. Рассмотрим выражение для максимальной работы расширения идеального газа в 5 процессах: Изобарном, изотермическом, адиабатическом, изохорном и изобарноизотермическом. 1. Изобарный процесс осуществляется при постоянном давлении (р=const). При этом из уравнения (2) получаем. 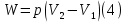 Учитывая что 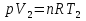 и и 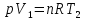 , имеем , имеем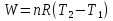 2. Изотермический процесс протекает при постоянной температуре (T=const). Подставляя в уравнение (2) в место p величину nRT/V из (3), получаем после интегрирования 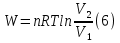 учитывая, что при T=const 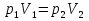 , получим , получим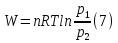 3. Адеабатический процесс отвечает условию Q=0. В этом процессе одновременно изменяются температура и давление газа. В связи с тем, что газ не получает теплоты из вне, работа адиабатического расширения производится за счет уменьшения внутренней энергии и газ охлаждается: W=- 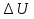 (8). (8).Приращение внутренней энергии зависит от молярной теплоемкости идеального газа при постоянном объеме 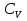 , т.е. , т.е.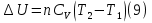 Из сравнения уравнений (8) и (9) получаем: 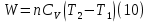 Где 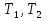 - начальная и конечная температура, соответственно. - начальная и конечная температура, соответственно. Для адиабатического процесса, пологая 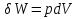 , получаем выражение , получаем выражение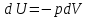 Но по (9) 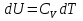 ; по(3) при n=1 р=RT/V, поэтому из (а) имеем ; по(3) при n=1 р=RT/V, поэтому из (а) имеем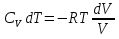 Или 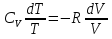 Учитывая, для идеального газа 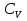 =const, получаем в результате интегрирования. =const, получаем в результате интегрирования. 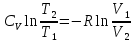 Откуда 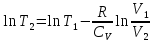 Между параметрами р, V, Т при протекании адиабатического процесса в идеальном газе имеют место соотношения р, V=const и Т,V=const, где 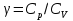 . .4. Изохорный процесс протекает при постоянном объеме (V=const). Из уравнения (2) получаем W=0. График в координатах р, V для 4 перечисленных процессах расширения или сжатия газа представлено на рисунке (1). Площадь под кривой соответствующего процесса дает мах работу расширения газа в этом процессе. 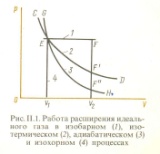 5. Изобарно-изотермический процесс отвечает условию, когда р=const и T=const. Если число молей n в смеси газов изменяется в результате химической реакции, например: 2СО+О2=2СО2, N2O4=2NO2 или в результате физического процесса, например при испарении жидкости, то протекает изобарно-изотермический процесс расширения или сжатия смеси газов при этом мах работа расширения идеального газа в соответствии с уравнением (4) равна 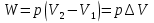 При р=const и T=const из уравнения (3) получаем 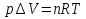 Отсюда 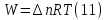 Где 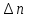 - приращение числа молей газов в результате реакции. - приращение числа молей газов в результате реакции.Величина 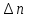 может иметь “+” “-” значения в зависимости от того, увеличивается или уменьшения число молей газов во время процесса. может иметь “+” “-” значения в зависимости от того, увеличивается или уменьшения число молей газов во время процесса. 9. Работа расширения для идеальных газов при адиабатическом процессе. Вывести уравнения адиабат. Термодинамика (греч. термо - «тепло», динамика - «сила») - раздел физики, изучающий соотношения и превращения теплоты и других форм энергии. В отдельные дисциплины выделились химическая термодинамика, изучающая физико-химические превращения, связанные с выделением или поглощением тепла, а также теплотехника. Для многих систем единственный вид работы – работа расширения. Практическое значение имеет обычно работа расширения газа, причем многие газы при достаточно низких давлениях и сравнительно высоких температурах приближенно подчиняются законам идеальных газов. При расширении газа совершается работа, которая вычисляется по уравнению: 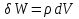 (1 )или в интегральной форме: (1 )или в интегральной форме: 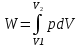 (2). (2). Для интегрирования уравнения (2) нужно знать зависимость между давлением и объемом газа, т.е. уравнение состоTяния газа. Эта зависимость для идеального газа описывается уравнением состояния Клапейрона-Менделеева: 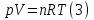 ; где n-количество идеального газа в молях; R-универсальная газовая постоянная, равная 8,314 ДЖ/(моль∙К). Рассмотрим выражения для максимальной работы расширения идеального газа в адиабатическом процессе. ; где n-количество идеального газа в молях; R-универсальная газовая постоянная, равная 8,314 ДЖ/(моль∙К). Рассмотрим выражения для максимальной работы расширения идеального газа в адиабатическом процессе.Адиабатический процесс отвечает условию Q=0. В этом процессе одновременно изменяются температура и давление газа. В связи с тем, что газ не получает теплоты извне, работа адиабатического расширения производится за счет уменьшения внутренней энергии и газ охлаждается: 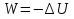 (4). (4). Приращение внутренней энергии зависит от молярной теплоемкости идеального газа при постоянном объеме 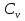 , т.е.: , т.е.: 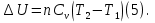 Из сравнения уравнений (4) и (5) получаем: 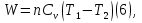 где где 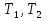 - начальная и конечная температура, соответственно. - начальная и конечная температура, соответственно. Из соотношения для адиабатического процесса, пологая 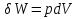 , получаемое выражение: , получаемое выражение: 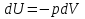 (7). (7). Но по (5) 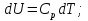 по (3) при по (3) при 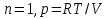 , поэтому имеем: , поэтому имеем: 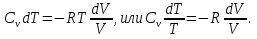 Учитыва, что для идеального газа 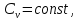 получаем в результате интегрирования: получаем в результате интегрирования: 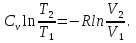 Откуда: Откуда: 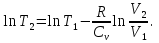 Между параметрами p, V, T при протекании адиабатического процесса в идеальном газе имеют место соотношения: 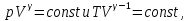 где где 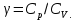 10. IIзакон термодинамики, формулировки. Основные понятия: самопроизвольные и не самопроизвольные процессы, обратимые и необратимые процессы. Постулат Планка. Расчет абсолютного значения энтропии. Термодинамика (греч. термо - «тепло», динамика - «сила») - раздел физики, изучающий соотношения и превращения теплоты и других форм энергии. В отдельные дисциплины выделились химическая термодинамика, изучающая физико-химические превращения, связанные с выделением или поглощением тепла, а также теплотехника. Второе начало термодинамики – это общий закон природы, действие которого простирается на самые разные системы. Второе начало термодинамики носит статистический характер и применимо только к системам из большого числа частиц, т.е. таким, поведение которых подчиняется законам статистики. Второе начало получило более полное физическое разъяснение в статистической термодинамике. Оно может быть выведено из постулатов статистической иермодинамики. Но это не противоречит сделанному утверждению: один постулат заменяется другим. Второе начало термодинамики, так же как и первое начало, является постулатом. 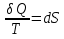 . . 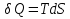 . . Процессы, которые совершаются в системе без вмешательства со стороны окружающей среды, называются самопроизвольными. Эти процессы протекают или в изолированной системе, или в неизолироанной, сопровождаясь уменьшением внутренней энергии системы и передачей энергии в окружную среду в форме теплоты или работы, или, наоборот, увелечением внутренней энергии за счет теплоты и работы полученной из окружающей среды. Процессы, которые без «вмешательства извне» сами собой совершаться не могут, называются несамопроизвольными, неестественными или отрицательными.Такие процессы не могут происходить в изолированной системе, так как для этого они требуют воздействия извне, сос стороны окружающей среды. Необратимыми процессами называются такие процессы, после протекания которых систему и окружающую среду одновременно нельзя вернуть в прежнее состояние. При необратимом процессе систему можно вернуть к первоначальному состоянию, но при этом в окружающей среде останутся некоторые изменения, «следы» необратимого процесса. Обратимыми процессами называются такие процессы, после которых можно вернуть и систему, и окражующую среду в прежнее состояние. При этом в обратном процессе система проходит через те же промежуточные состояния, что и в прямом процессе, но в обртном порядке. Постулат Планка: энтропия индивидуального кристаллического вещества при абсолютном нуле равна нулю: 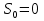 . Постулат Планка справедлив только для индивидуальных веществ, кристаллы которых идеально построены (в кристаллической решетке все узлы заняты молекулами или атомами, правильно чередующимися и закономерно ориентированными). Такие кристаллы называются идеальными твердыми телами. Реальные кристаллы не являются таковыми, так как их кристаллическая решетка построена не идеально. В соответствии с постулатом Планка уравнение для идеального твёрдого тела примет вид: . Постулат Планка справедлив только для индивидуальных веществ, кристаллы которых идеально построены (в кристаллической решетке все узлы заняты молекулами или атомами, правильно чередующимися и закономерно ориентированными). Такие кристаллы называются идеальными твердыми телами. Реальные кристаллы не являются таковыми, так как их кристаллическая решетка построена не идеально. В соответствии с постулатом Планка уравнение для идеального твёрдого тела примет вид: 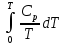 . . 11. II закон термодинамики для обратимых и необратимых процессов. Свойства энтропии. Термодинамика (греч. термо - «тепло», динамика - «сила») - раздел физики, изучающий соотношения и превращения теплоты и других форм энергии. В отдельные дисциплины выделились химическая термодинамика, изучающая физико-химические превращения, связанные с выделением или поглощением тепла, а также теплотехника. II закон термодинамики для обратимых процессов. Найдем зависимость функции состояния энтропии от теплоты для обратимых процессов. Запишем уравнение первого начала термодинамики для процесса с бесконечно малыми изменениями параметров: 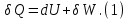 Если процесс обратимый и совершается только механическая работа против сил внешнего давления, то Если процесс обратимый и совершается только механическая работа против сил внешнего давления, то 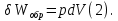 Рассмотрим 1моль идеального газа. Учитывая, что Рассмотрим 1моль идеального газа. Учитывая, что 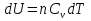 , можно записать уравнение (1) в виде: , можно записать уравнение (1) в виде: 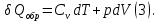 Если для идеального газа Если для идеального газа 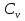 не зависит от объема, получим не зависит от объема, получим 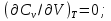 из уравнения состояния идеального газа из уравнения состояния идеального газа 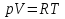 находим находим 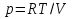 и и 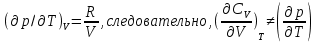 (4). (4). Таким образом 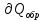 не является полным дифференциалом. На примере идеального газа докажем, что если обе части равенства (3) разделив на Т, то не является полным дифференциалом. На примере идеального газа докажем, что если обе части равенства (3) разделив на Т, то 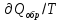 приобретает свойства полного дифференциала. Для идеального газа из соотношения приобретает свойства полного дифференциала. Для идеального газа из соотношения 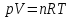 имеем: имеем: 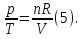 Тогда уравнение (3) для одного моля газа примет вид:  Разделив обе части уравнения (6) на Т, олучим: 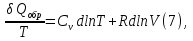 где где 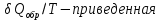 теплота. Из уравнения видно, что: теплота. Из уравнения видно, что: 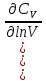 Уравнение (8) справедливо не только для идеального газа, но для любой системы. Из этого уравнения следует, что для всех систем: 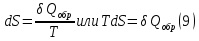 . Уравнение (9) представляет собой математическую формулировку второго начала термодинамики для обратимых процессов. В любых круговых процессах изменение энтропии, как и любых других функций состояния, равно нулю: . Уравнение (9) представляет собой математическую формулировку второго начала термодинамики для обратимых процессов. В любых круговых процессах изменение энтропии, как и любых других функций состояния, равно нулю: 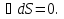 Отсюда в соответствии с уравнением (9): Отсюда в соответствии с уравнением (9):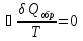 ; (10). ; (10).Математическая формулировка второго начала термодинамики для обратимых процессов. Пусть из состояния 1 в состояние 2 система может перейти как посредством необратимого процесса, так и обратимого (рисунок). Согласно первому началу термодинамики для необратимого процесса получаем: 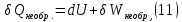 а для обратимого процесса: а для обратимого процесса: 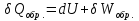 (12). Вычитая из (11) уравнение (12), получим для кругового процесса: (12). Вычитая из (11) уравнение (12), получим для кругового процесса: 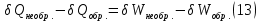 Выражение (13) может быть равно нулю, больше нуля. Если оба процесса обраимы, то уравнение равно нулю, так как после проведения обратимого процесса в прямом и обратном направлениях никаких изменений в самой системе, ни в окружающей среде не происходит. Если обе части равенства больше нуля, то это означает, что единственным результатом кругового процесса будет поглощение теплоты из окружающей среды и совершение системой эквивалентного количества работы, т.е. полное превращение теплоты в работу, что противоречит второму началу термодинамики. Если обе разности в уравнении (13) меньше нуля, то это не противоречит второму началу термодинамики, потому что единственным результатом будет полное превращение работы в теплоту. Таким образом, непосредственным следсвием второго начала термодинамики и определения необратимых процессов являются два неравенства: 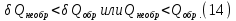 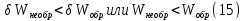 Из (15) следует, что работа любого необратимого процесса всегда меньше работы обратимого процесса между теми же начальными и конечными состояниями сиситемы. Потому работу в обратимых процессах называют максимальной работой: 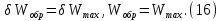 Чем меньше работа по сравнению с максимальной6 тем более необратим процесс. Процессы, которые происходят без совершения работы, называются необратимыми. Найдем соотношение между изменением энтропии и теплотой, передаваемой в необратимом процессе. Теплота в необратимом процессе согласно уравнению (14) меньше чем в обратимом. При этом из уравнения (9) получаем: 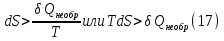 или или 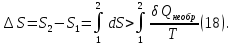 Для необратимых самопроихвольных процессов в изолированной системе Для необратимых самопроихвольных процессов в изолированной системе 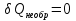 и из (17) получаем: и из (17) получаем: 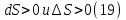 . При изотермических необратимых процессах (T=const) . При изотермических необратимых процессах (T=const) 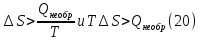 . . Для цикллов, включающих необратимые процессы, из (17) и (10) получаем соотношение: 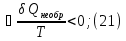 Уравнения (17) – (21) представляют собой выражения второго начала термодинамики для необратимых процессов. Для необратимых процессов второе начало термодинамики – это закон существования и возрастания энтропии. Как следует из уравнения (19), при протекании необратимого процесса в изолированной системе энтропия возрастает. Объединяя соотношения (17) и (9) выражающие второй закон термодинамики для обратимых и необратимых процессов, можно записать: 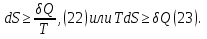 Знак равенства соответствует обратимым процессам, знак неравенства – необратимым. Для изолированных систем Знак равенства соответствует обратимым процессам, знак неравенства – необратимым. Для изолированных систем 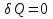 и из неравенства (20) получим: и из неравенства (20) получим: 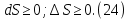 Полставляя в уравнение (23) значение 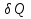 из соотношения из соотношения 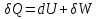 получим объединенное уравнение первого и второго начала термодинамики: получим объединенное уравнение первого и второго начала термодинамики: 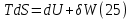 12.Расчет изменения энтропии для различных физико-химических процессов: нагревание, фазовые переходы, смешение идеальных газов, изобарный, изотермический, изохорныйпроцессы. Термодинамика (греч. термо - «тепло», динамика - «сила») - раздел физики, изучающий соотношения и превращения теплоты и других форм энергии. В отдельные дисциплины выделились химическая термодинамика, изучающая физико-химические превращения, связанные с выделением или поглощением тепла, а также теплотехника. |
