шпоры фх. 1. Физическая химия цель, задачи, методы исследования. Основные понятия физической химии. Физ химия
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
|
1. Физическая химия: цель, задачи, методы исследования. Основные понятия физической химии. Физ. химия- наука о закономерностях хим.процессов и хим. явлений. Предмет физ.химии объяснение хим. явлений на основе более общих законов физики. Физ.химия рассматривает две основные группы вопросов: 1. Изучение строения и свойств вещества и составляющих его частиц; 2. Изучение процессов взаимодействия веществ. Физ.химия ставит целью изучение связей м/у хим-ми и физ-ми явлениями. Знание таких связей необходимо для того, чтобы глубже изучить хим.реакции, протекающие в природе и используемые в технолог. процессах, управлять глубиной и направлением реакции. Основной целью дисциплины Физ.химия изучение общих связей и закономерностей хим. процессов, основанных на фундаментальных принципах физики. Физ.химия применяет физ. теории и методы к хим.явлениям. Она объясняет ПОЧЕМУ и КАК происходят превращения веществ: хим. реакции и фазовые переходы. 2.хим.термодинамика – это наука о взаимосвязи хим.реакций с физич явлениями, которые сопровождают эти энергии. Это наука о взаимном влиянии физич. Условий и механизма хим реакций. Основные понятия физ.химии Основной объект хим. термодинамики –это термодинамическая система. Термодинамич. система – любое тело или совокупность тел, способных обмениваться м/у собой и с др. телами энергией и в-вом. Системы подразделяют на открытые, закрытые и изолированные. Открытая-термодинамическая система обменивается с внешней средой и в-вом и энергией. Закрытая -система, в которой отсутствует обмен в-вом с окружающей средой, но она может обмениваться с ней энергией. Изолированная-система объем остается постоянным и лишена возможности обмениваться с окружающей средой и энергией и в-вом. Система может быть гомогенной (однородной) или гетерогенной (неоднородной). Фаза- это часть системы, которая в отсутствии внешнего поля сил обладает одинаковым составом во всех своих точках и одинаковыми термодинамич. св-вами и отделена от других частей системы поверхностью раздела. Фаза всегда однородна, т.е. гомогенна, поэтому однофазная система называется гомогенной. Система, состоящая из неск-ких фаз, называется гетерогенной. Свойства системы подразделить на две группы: экстенсивные и интенсивные. В термодинамике используются понятия равновесных и обратимых процессов. Равновесным –это процесс, проходящий через непрерывный ряд состояний равновесия. Обратимый термодинамический процесс – это процесс, который может быть проведен в обратном направлении без того, чтобы в системе и окружающей среде остались какие-либо изменения. 3. Внутр. энергия системы- это сумма потенциальной энергии взаимодейст. всех частиц тела м/у собой и кинетической энергии их движения (без учета кинетич. и потенциальн. энергий системы в целом). Внут. энергия системы зависит от природы в-ва, его массы и от параметров состоянии системы. Она возраст. с увеличением массы системы, так как является экстенсивным св-вом системы. Внутр. энергию обозначают литерой U и выражают в джоулях (Дж). В общем случае для системы с кол-вом в-ва 1 моль. Внутр. энергия, как и любое термодинамич. св-во системы, явл-ся функцией сост. Непосредственно в эксперименте проявляются только изменения внутр. энергии. Именно поэтому при расчетах всегда оперируют с её изменением U2 –U1 = U. Все изменения внутр. энергии делятся на две группы. В 1-ую группу входит только 1-а форма перехода движения путем хаотических столкновений молекул двух соприкасающихся тел, т.е. путём теплопроводности (и одновременно путём излучения). Мерой передаваемого таким способом движения является теплота. Понятие теплоты связано с поведением огромного числа частиц – атомов, молекул, ионов. Они находятся в постоянном хаотическом (тепловом) движении. Теплота – форма передачи энергии. Второй способ обмена энергией – работа. Этот обмен энергии обусловлен действием, совершаемым системой, или действием, совершаемым над ней. Обычно работу обозначают символом W. Работа, также как и теплота, не является функцией состояния системы, поэтому величину, соответствующую бесконечно малой работе, обозначают символом частной производной -  W. W.4. I-ый закон термодинамики. Первое начало термодинамики непосредственно связано с законом сохранения энергии. Исходя из этого закона, следует, что в любой изолированной системе запас энергии остается постоянным. Из законасохранения энергии вытекает еще одна формулировка первого начала термодинамики – невозможность создания вечного двигателя (perpetuum mobile) первого рода, который производил бы работу, не затрачивая на это энергии. Особенно важной для химической термодинамики формулировкой первого начала является выражение его через понятие внутренней энергии: внутренняя энергия является функцией состояния, т.е. её изменение не зависит от пути процесса, а зависит только от начального и конечного состояния системы. Изменение внутренней энергии системы U может происходить за счет обмена теплотой Q и работой W с окружающей средой. Тогда из закона сохранения энергии следует, что полученная системой извне теплота Q расходуется на приращение внутренней энергии ΔU и работу W, совершенную системой, т.е. Q = ΔU +W . Данное уравнение является математическим выражением первого начала термодинамики. I начало термодинамики его формулировки: в любой изолированной системе запас энергии остается постоянным; разные формы энергии переходят друг в друга в строго эквивалентных количествах; вечный двигатель (perpetuummobile) первого рода невозможен; внутренняя энергия является функцией состояния, т.е. её изменение не зависит от пути процесса, а зависит только от начального и конечного состояния системы. аналитическое выражение: Q = DU +W ; для бесконечно малого изменения величин dQ = dU + dW. 1-ое начало термодинамики устанавливает соотнош. м/у теплотой Q, работой А и изменением внутр. энергии системы ΔU. Изменение внутр. энергии системы равно кол-ву сообщенной системе теплоты минус кол-во работы, совершенной системой против внешних сил. (I.1) (I.2) Уравнение (I.1)- математическая запись 1-го начала термодинамики, уравнение (I.2) – для бесконечно малого изменения сост. системы. Внутр. энергия- функция сост.; это означает, что измен-е внутр. энергии ΔU не зависит от пути перехода системы из состояния 1 в состояние 2 и равно разности величин внутр. энергии U2 и U1 в этих состояниях: (I.3) 6 .Следствия первого начала термодинамики ( изохорный и изобарный процессы). Способы записи теплот химических реакций. энтальпия Химическая термодинамика изучает энергетические эффекты химических процессов; позволяет определить возможность, направление и глубину протекания химического процесса в конкретных условиях. Следствие из I начала термодинамики. Внутренняя энергия, энтальпия, связь между ними: DH = DU + PDV. dQV=dU dQP=dH Для изохорного и изобарного процессов теплота процесса приобретает свойства функции состояния. Это положение сформулировано на основании опытных данных Г.И. Гессом и называется законом Гесса. Закон Гесса – математическое следствие I закона термодинамики. Закон Гесса: тепловой эффект реакции не зависит от пути процесса (промежуточных стадий), а определяется только начальным и конечным состояниями системы, т.е. состоянием исходных веществ и продуктов реакции. Расчет теплот химических реакций по стандартным теплотам образования и сгорания. Изохорный процесс (V = const; ΔV = 0). Поскольку работа расширения равна произведению давления и изменения объема, для изохорного процесса получаем: (I.1) (I.2) (I.3) Следовательно при const=V вся теплота подведенная к системе расходуется на увеличение внутренней энергии или все изменение внутренней энергии обращается в теплоту. Изобарный процесс (Р = const). Подставляя полученные выражения для работы различных процессов в уравнение (I.1), для тепловых эффектов этих процессов получим: (I.5); В уравнении (I.7) сгруппируем переменные с одинаковыми индексами. Получаем: Введем новую функцию состояния системы – энтальпию H, тождественно равную сумме внутренней энергии и произведения давления на объем: Тогда выражение (I.8) преобразуется к следующему виду: (I.9) Т.о., тепловой эффект изобарного процесса равен изменению энтальпии системы. При этом теплота приобретает св-ва функции обозначается символом 4. Закон Гесса, его следствия. Взаимосвязь между тепловым эффектом химической реакции при постоянном объеме и давлении. Как известно, большинство хим. реакций сопровождаются выделением (экзотермические реакции) либо поглощением (эндотермические реакции) теплоты. Первое начало термодинамики дает возможность рассчитать тепловой эффект хим. реакции при различных условиях её проведения. Тепловой эффект (теплота) химической реакции – количество теплоты, выделившейся либо поглотившейся в ходе реакции. Тепловой эффект относят, как правило, к числу молей прореагировавшего исходного вещества, стехиометрический коэффициент перед которым максимален. Например, реакцию окисления водорода в хим. термодинамике записывают в виде: Н2 + 1/2 О2 ––> Н2О и тепловой эффект рассчитывают на 1 моль водорода. Теплота образования вещества – тепловой эффект реакции образования 1 моля сложного вещества из простых. Теплоты образования простых в-в принимаются равными нулю. Теплота сгорания вещества – тепловой эффект реакции окисления 1 моля в-ва в избытке кислорода до высших устойчивых оксидов. Закон Гесса, является частным случаем первого начала термодинамики: Тепловой эффект химической реакции, проводимой в изобарно-изотермических или изохорно-изотермических условиях, зависит только от вида и состояния исходных веществ и продуктов реакции и не зависит от пути её протекания. Закон Гесса: тепловой эффект реакции не зависит от пути процесса (промежуточных стадий), а определяется только начальным и конечным состояниями системы, т.е. состоянием исходных веществ и продуктов реакции. Выше было показано, что изменение энтальпии ΔН (тепловой эффект изобарного процесса Qp) и изменение внутр. энергии ΔU (тепловой эффект изохорного процесса Qv) не зависят от пути, по которому система переходит из начального состояния в конечное. Практическое значение закона Гесса состоит в том, что он позволяет рассчитывать тепловые эффекты хим. процессов. Тепловой эффект хим. реакции равен разности сумм теплот образования продуктов реакции и исходных в-в, умноженных на стехиометрические коэффициенты. Следствия закона Гесса: Тепловой эффект хим. реакции равен разности сумм теплот сгорания исходных в-в и продуктов реакции, умноженных на стехиометрические коэффициенты. 5. Теплоемкость, виды. Взаимосвязь между теплоемкостью при p=const, V=const (уравнение Майера). Теплоемкостью называют количество теплоты, которое необходимо сообщить системе для её нагревания на 1 К в условиях отсутствия полезной работы. Различают удельную и молярную теплоемкости. У дельной теплоемкостью С называют количество теплоты, необходимое для нагревания единицы массы вещества на 1К, а молярной теплоемкостью С – количество теплоты, необходимое для нагревания одного моля вещества на 1К. Различают истинную и среднюю теплоемкости. Под истинной теплоемкостью понимают отношение бесконечно малого количества теплоты, полученного системой, к бесконечно малому приращению температуры, которое при этом наблюдается: C = Q/dT. Средней молярной теплоемкостью С в интервале температур от Т1 и Т2 называют отношение конечного количества теплоты, подведенного к одному молю вещества, к разности температур Т2-Т1: 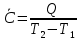 Количество теплоты, переданное телу при постоянном объеме, равно приращению внутренней энергии тела 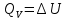 . Количество теплоты, переданное телу припостоянном давлении, равно приращению энтальпии тела . Количество теплоты, переданное телу припостоянном давлении, равно приращению энтальпии тела 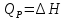 . Отсюда для истинной молярной теплоемкости при постоянном объеме и давлении получаем выражение: . Отсюда для истинной молярной теплоемкости при постоянном объеме и давлении получаем выражение: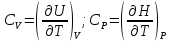 Если постоянство объема или давления указано, то частную производную по температуре можно заменить полной производной и написать (для n молей вещества): При V=const QV = dU = n  dT dTПри p=const QР = dH = n  dT dTВ расчетах  определяют по опытным данным для определяют по опытным данным для  и наоборот. Для этого нужно знать разность теплоемкостей и наоборот. Для этого нужно знать разность теплоемкостей 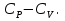 Для твердых и жидких тел разность 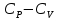 мала, так как их объем почти не меняются от температуры. мала, так как их объем почти не меняются от температуры.Для газов разность 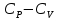 достаточна велика и ее нужно учитывать. Внутренняя энергия идеального газа не зависит от объема и давления. Продифференциировав состояние одного моля идеального газа, получаем соотношение: достаточна велика и ее нужно учитывать. Внутренняя энергия идеального газа не зависит от объема и давления. Продифференциировав состояние одного моля идеального газа, получаем соотношение: 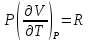 Подставляем полученное выражение, получаем уравнение Майера для идеального газа: CP - CV = R = 8,314 Дж/(моль*К) 6. Зависимость теплоемкости от температуры. Взаимосвязь между средней и истинной теплоемкостями неорганического вещества p=const (вывод пояснение). Теплоемкостью называют количество теплоты, которое необходимо сообщить системе для её нагревания на 1 К в условиях отсутствия полезной работы. Для многих термодинамических расчетов нужно знать значения теплоемкости веществ, участвующих в реакции и зависимость теплоемкости веществ от температуры. Теплоемкости веществ при разных температурах определяются из опыта или вычисляются теоретически. Опытные значения теплоемкости при разных температурах обычно представляют в виде следующих интерполяционных уравнений: 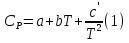 Или 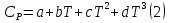 Где a, b, 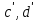 - коэффициенты. - коэффициенты.Интерполяционные уравнения(1) и (2) пригодны только в том интервале температур, в котором они изучены экспериментально. Молекулярную теплоемкость при постоянном объеме 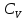 вычисляют по уравнениям используя численные значения вычисляют по уравнениям используя численные значения 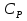 , найденные по итерполяционным уравнениям (1) или (2). , найденные по итерполяционным уравнениям (1) или (2).В термодинамических расчетах часто приходиться вычислять среднюю теплоемкость по данным для истинной теплоемкости при разных температурах и наоборот. Установим зависимость между истинной и средней теплоемкостями при постоянном давлении. Подставляя в выражение, получаем уравнение для вычисления средней молярной теплоемкости в данном интервале температур, зная истинные теплоемкости 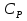 : :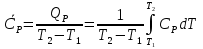 (3) (3)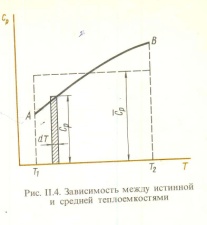 Расчет Расчет  можно провести графически и аналитически, если известны значения истинной теплоемкости при нескольких температурах, то среднюю теплоемкость удобнее рассчитывать графически. На рисунке зависимость можно провести графически и аналитически, если известны значения истинной теплоемкости при нескольких температурах, то среднюю теплоемкость удобнее рассчитывать графически. На рисунке зависимость  представлена кривой АВ. Интеграл представлена кривой АВ. Интеграл  в уравнении (3) представляет собой площадь в уравнении (3) представляет собой площадь  под кривой АВ. Средняя теплоемкость под кривой АВ. Средняя теплоемкость 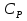 является высотой прямоугольника с основанием является высотой прямоугольника с основанием 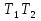 , равновеликого площади , равновеликого площади 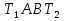 . Таким образом, измерив площадь . Таким образом, измерив площадь 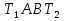 под кривой АВ определяем среднюю теплоемкость под кривой АВ определяем среднюю теплоемкость 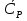 по уравнению: по уравнению: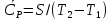 Где S – площадь 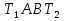 . При этом площадь нужно выразить в Дж/моль. Аналитическую среднюю теплоемкость можно рассчитать по (3), если известна зависимость истинной теплоемкости от температуры: . При этом площадь нужно выразить в Дж/моль. Аналитическую среднюю теплоемкость можно рассчитать по (3), если известна зависимость истинной теплоемкости от температуры: 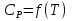 . Подставляя уравнение (1) или (2) в (3) получаем выражения: . Подставляя уравнение (1) или (2) в (3) получаем выражения: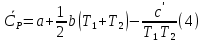 Или 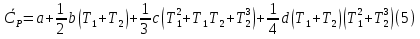 Истинную теплоемкость можно рассчитать по опытным данным для средней теплоемкости при разных температурах. Перепишем равенства (3) считая температуру 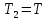 переменной величиной: переменной величиной: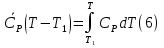 Известно, что производная от определенного интеграла по верхнему пределу при постоянном нижнем пределе интегрирования равна подынтегральной функции, поэтому, взяв производную по температуре от уравнения (6), получим: 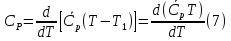 Средняя теплоемкость 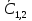 в интервале температур от в интервале температур от 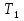 до до 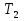 вычисляется по уравнению: вычисляется по уравнению: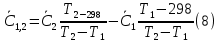 Где 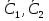 - средние теплоемкости в интервале температур от 298 К до - средние теплоемкости в интервале температур от 298 К до 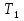 и от 298 К до и от 298 К до 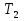 . Уравнение (8) является следствием уравнения (6) и известного свойства определенного интеграла: . Уравнение (8) является следствием уравнения (6) и известного свойства определенного интеграла: 7. Зависимость тепловых эффектов химических реакций от температуры. Уравнение Киргоффа. Определение  реакции при нестандартной температуре. реакции при нестандартной температуре.Рассмотрим зависимость теплоты процесса при постоянном давлении от температуры. Возьмем частную производную по температуре от теплоты процесса  Н при постоянном давлении или от теплоты процесса Н при постоянном давлении или от теплоты процесса  U при постоянном объеме: U при постоянном объеме: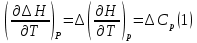 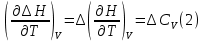 Отсюда получаем 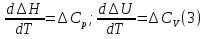 Где 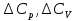 - изменение молярной теплоемкости в результате протекания процесса при p=const или V=const. - изменение молярной теплоемкости в результате протекания процесса при p=const или V=const.Уравнение (3) называют уравнениями Киргоффа; из них следует, что температурный коэффициент процесса (теплового эффекта реакции, фазового перехода и т.д.) равен изменению теплоемкости в результате протекания этого процесса. Для химической реакции 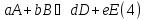 изменение теплоемкости (при постоянном давлении изменение теплоемкости (при постоянном давлении 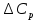 ) определяется выражением ) определяется выражением 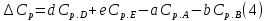 или 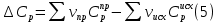 где 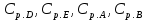 - молярные теплоемкости реагентов при постоянном давлении; - молярные теплоемкости реагентов при постоянном давлении; 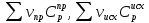 - сумма теплоемкостей соответственно продуктов реакции и исходных веществ с учетом стехиометрических коэффициентов. - сумма теплоемкостей соответственно продуктов реакции и исходных веществ с учетом стехиометрических коэффициентов.Из уравнения (3) следует, что если изменение теплоемкости 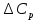 во время процесса положительно, то и тепловой эффект с ростом температуры становится более положительным : во время процесса положительно, то и тепловой эффект с ростом температуры становится более положительным :При 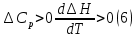 и наоборот при 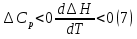 Если теплоемкость во время процесса не меняется, т.е. сумма теплоемкостей продуктов реакции равна сумме теплоемкостей исходных веществ , то тепловой эффект процесса согласно (3) не зависит от температуры: При 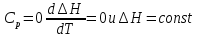 Аналогичные равенства получаются для теплового эффекта 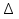 U процесса, протекающего при постоянном объеме, Изменение теплоемкости при фазовом переходе, например в процессе плавления одного моля вещества U процесса, протекающего при постоянном объеме, Изменение теплоемкости при фазовом переходе, например в процессе плавления одного моля вещества 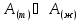 , определяют по уравнению , определяют по уравнению 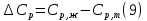 где 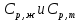 - молярные теплоемкости при постоянном давлении вещества А в жидком и твердом состояниях (при температуре плавления). - молярные теплоемкости при постоянном давлении вещества А в жидком и твердом состояниях (при температуре плавления).Для вычисления теплового эффекта процесса 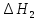 при при 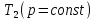 , если известен тепловой эффект процесса , если известен тепловой эффект процесса 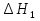 при при 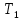 , уравнение Киргофа (3) нужно проинтегрировать , уравнение Киргофа (3) нужно проинтегрировать 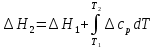 (10). (10).Аналогичное выражение получается для теплового эффекта процесса при постоянном объеме. При использовании уравнения (10) нужно иметь в виду, что в температурном интервале от 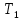 до до 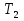 не должно быть фазовых переходов веществ, участвующих в реакции. не должно быть фазовых переходов веществ, участвующих в реакции.Если известны теплоемкости исходных веществ и продуктов реакции в данном интервале температур, то тепловой эффект можно вычислить графически. Для этого определяют значения 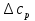 по уравнению (8) при нескольких температурах и строят график в координатах по уравнению (8) при нескольких температурах и строят график в координатах 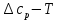 . . 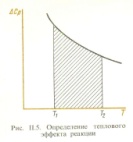 Интеграл Интеграл 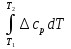 равен площади под кривой в интервале температур от равен площади под кривой в интервале температур от 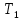 до до 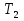 . .Для аналитического вычисления теплового эффекта по уравнению (10) нужно знать зависимость 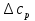 от температуры. от температуры.Считая приближенно 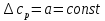 , из уравнения (10) получаем , из уравнения (10) получаем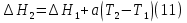 или, принимая или, принимая 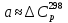 , , 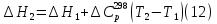 . .Более грубым приближением будет допущение, что 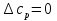 . Учитывая (10), получаем . Учитывая (10), получаем 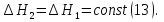 Предположение 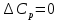 равносильно допущению, что тепловой эффект реакции не зависит от температуры. равносильно допущению, что тепловой эффект реакции не зависит от температуры. Более точные результаты получается, если в расчетах использовать в расчетах интерполяционные уравнения. При этом для зависимости 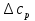 от температуры согласно уравнению (6) получаем от температуры согласно уравнению (6) получаем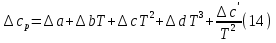 Подставляя уравнения (14) в (10), после интегрирования находим 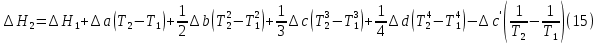 или, если взять неопределенный интеграл, то вместо (15) получим 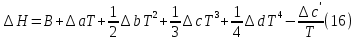 где В – постоянная интегрирования, которая определяется обычно по значению теплового эффекта при стандартных условиях (298 К и 0,1018 МПа). Следует заметить, что интерполяционное уравнение (16) справедливо только в том интервале температур, для которого опытным путем найдены коэффициенты в уравнении (14) для теплоемкостей. 8. Работа расширения для идеальных газов при изобарном, изохорном, изотермическом процессах. |
