шпоры фх. 1. Физическая химия цель, задачи, методы исследования. Основные понятия физической химии. Физ химия
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
|
Зависимость константы равновесия от температуры. Уравнения изобары и изохоры Вант-Гоффа Зависимость константы равновесия реакции от температуры описывается уравнением Вант-Гоффа, называемом изобарой Вант-Гоффа: 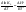 или или 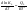 или изохорой Вант-Гоффа: 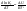 или или 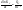 . . Знак теплового эффекта определяется знаком производной 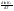 в уравнении изобары Вант-Гоффа. Поэтому: в уравнении изобары Вант-Гоффа. Поэтому:- если H0 0, т.е. химическая реакция протекает с поглощением тепла. Данная реакция эндотермическая; знак производной будет положительным. Следовательно, константа равновесия возрастает с увеличением температуры; - если H0 0, т.е. химическая реакция идет с выделением тепла; знак производной будет отрицательным. Следовательно, константа равновесия с увеличением температуры уменьшается; - если H0 = 0, химическая реакция идет без теплового эффекта, константа равновесия в данном случае не зависит от температуры. 25) Расчёт теп.эф х.р. на основе изобары Вант-Гоффа (расчётный и граф. способы). Теп.эф.х.р. наз.кол-во теплоты,которое выд-ся или поглощается при необратимом протекании реакции,когда ед. работой яв-ся только работа расширения.При этом тем-ры исх.в-в должны быть одинаковыми.Теп.эф х.р. при постоянном объёме (изохорный процесс) равен приращению внутр.эн.системы во время реакции;теп.эф. х.р. при постоянном давлении (изобарный процесс)равен приращению энтальпии во время этой реакции: Qv= 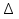 U; Qp= U; Qp=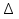 H. H.Для бесконечно малогоизменения теплоты в изохорном и изобарном процессах можно написать: 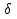 Qv=dU; Qv=dU; 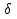 Qp=dH. Qp=dH.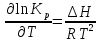 ; ;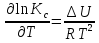 , Эти ур-я выр-ют завис-ть константы равновесия х.р. протекающей при P и V=const от T , Эти ур-я выр-ют завис-ть константы равновесия х.р. протекающей при P и V=const от T и наз-ся ур-ми изобары и изохоры Вант-Гоффа. и наз-ся ур-ми изобары и изохоры Вант-Гоффа.Левая часть ур-я пред-ет собой тем.коэф.константы равновесия знак которой опр-ся знаком измен-я энтальпии или внутр. эн-гии:1)Х.р. протекает с выд-ем тепла т.е. 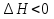 ,то с повыш.t ,то с повыш.t константа равновесия умень-ся т.е. константа равновесия умень-ся т.е.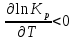 , ,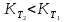 ;2) Х.р. протекает с поглощ-ем тепла т.е. ;2) Х.р. протекает с поглощ-ем тепла т.е. 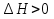 ,то с повыш.t ,то с повыш.t константа равновесия увель-ся т.е. константа равновесия увель-ся т.е.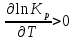 , ,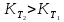 ;3) ;3)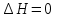 след-но след-но 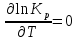 , , 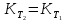 .Любая физ.-хим. система наход-ся в равновесии стремится сохранить его,и на любое воздействие направ-ное на нарушение сос-я равновесия отвечает возникновением процессов внутри системы стремящихся ослабить это воздействие. .Любая физ.-хим. система наход-ся в равновесии стремится сохранить его,и на любое воздействие направ-ное на нарушение сос-я равновесия отвечает возникновением процессов внутри системы стремящихся ослабить это воздействие.Интегрированные формы ур-я изобары В-Г и их исполь-ие для расчетов. После разделения переменных в ур-е изобары В-Г: 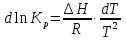 (1) (1)Неопр-ое интег-ние ур-я (1) даёт след. вид ур-я: 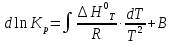 (2), где В-пост. интег-ния. (2), где В-пост. интег-ния.В узком интервале t  можно считать,что теп.эф.х.р. не зависит от t можно считать,что теп.эф.х.р. не зависит от t тогда тогда 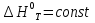 отсюда след-ет интег-ние ур-я (2) примет вид: отсюда след-ет интег-ние ур-я (2) примет вид: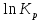 = =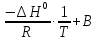 (3) (3) 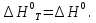 Граф-ки ур-е (2) пред-ет собой прямую линию в коор-тах: 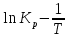 ,отсюда ,отсюда tg 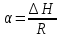 и и 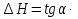 R. R.Опр-ое интег-ние ур-я (1) в интервале тем-р 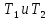 даёт даёт 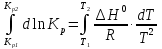 (4).Если считать,что в интервале тем-р (4).Если считать,что в интервале тем-р 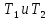 теп.эф.х.р. не зависит от t теп.эф.х.р. не зависит от t то после интег-я мы получим ур-е: то после интег-я мы получим ур-е: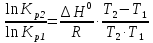 (5)(применяется для рассчётов). (5)(применяется для рассчётов).26) Расчёт теп.эф х.р. на основе изохоры Вант-Гоффа (расчётный и граф. способы). Теп.эф.х.р. наз.кол-во теплоты,которое выд-ся или поглощается при необратимом протекании реакции,когда ед. работой яв-ся только работа расширения.При этом тем-ры исх.в-в должны быть одинаковыми.Теп.эф х.р. при постоянном объёме (изохорный процесс) равен приращению внутр.эн.системы во время реакции;теп.эф. х.р. при постоянном давлении (изобарный процесс)равен приращению энтальпии во время этой реакции: Qv= 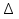 U; Qp= U; Qp=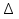 H. H.Для бесконечно малогоизменения теплоты в изохорном и изобарном процессах можно написать: 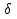 Qv=dU; Qv=dU; 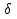 Qp=dH. Qp=dH.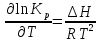 ; ;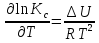 , Эти ур-я выр-ют завис-ть константы равновесия х.р. протекающей при P и V=const от T , Эти ур-я выр-ют завис-ть константы равновесия х.р. протекающей при P и V=const от T и наз-ся ур-ми изобары и изохоры Вант-Гоффа. и наз-ся ур-ми изобары и изохоры Вант-Гоффа.Левая часть ур-я пред-ет собой тем.коэф.константы равновесия знак которой опр-ся знаком измен-я энтальпии или внутр. эн-гии:1)Х.р. протекает с выд-ем тепла т.е. 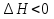 ,то с повыш.t ,то с повыш.t константа равновесия умень-ся т.е. константа равновесия умень-ся т.е.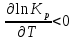 , ,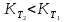 ;2) Х.р. протекает с поглощ-ем тепла т.е. ;2) Х.р. протекает с поглощ-ем тепла т.е. 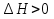 ,то с повыш.t ,то с повыш.t константа равновесия увель-ся т.е. константа равновесия увель-ся т.е.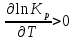 , ,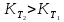 ;3) ;3)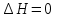 след-но след-но 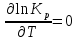 , , 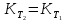 .Любая физ.-хим. система наход-ся в равновесии стремится сохранить его,и на любое воздействие направ-ное на нарушение сос-я равновесия отвечает возникновением процессов внутри системы стремящихся ослабить это воздействие. .Любая физ.-хим. система наход-ся в равновесии стремится сохранить его,и на любое воздействие направ-ное на нарушение сос-я равновесия отвечает возникновением процессов внутри системы стремящихся ослабить это воздействие.Интегрированные формы ур-я изохоры В-Г и их исполь-ие для расчетов. После разделения переменных в ур-е изохоры В-Г: 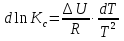 (1) (1)Неопр-ое интег-ние ур-я (1) даёт след. вид ур-я: 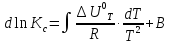 (2), где В-пост. интег-ния. (2), где В-пост. интег-ния.В узком интервале t  можно считать,что теп.эф.х.р. не зависит от t можно считать,что теп.эф.х.р. не зависит от t тогда тогда 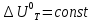 отсюда след-ет интег-ние ур-я (2) примет вид: отсюда след-ет интег-ние ур-я (2) примет вид: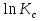 = =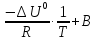 (3) (3) 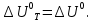 Граф-ки ур-е (2) пред-ет собой прямую линию в коор-тах: 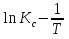 ,отсюда ,отсюда tg 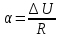 и и 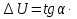 R. R.Опр-ое интег-ние ур-я (1) в интервале тем-р 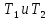 даёт даёт 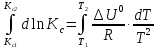 (4).Если считать,что в интервале тем-р (4).Если считать,что в интервале тем-р 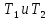 теп.эф.х.р. не зависит от t теп.эф.х.р. не зависит от t то после интег-я мы получим ур-е: то после интег-я мы получим ур-е: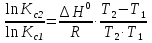 (5)(применяется для расчетов). (5)(применяется для расчетов).27)Фазовые равновесия основные опр-я: Термодин.теория фазовых равновесий и р-ров позволяет на основе опытных данных по диаграммам состояния теор.предвидеть и рассчитать условия для получения нужных продуктов путём испарения,крист-ции,экстракции и др.фаз.переходов. Фаза-совокупность частей системы,обладающих одинаковыми термодин.св-вами и отделённых от др.частей поверх-тями раздела. Составляющие в-ва системы(компоненты)-индивидуальные хим.в-ва,которые могут быть выделены из системы и существовать вне её. Фазовое равновесие(гетерогенное)-равновесие в системе,состоящей из нескольких фаз. Правило фаз Гиббса:число степеней свободы (независимых параметров)системы,на которую влияют только Т и Р,равно числу независимых компонентов минус число фаз плюс два:F=K-Ф+2. Св-ва конден.систем прак-ки не зависят от Р,поэтому числов внеш. факторов умен-ся на ед.,а по правилу фаз опр-ся так называемая условная вариантность системы:F=K-Ф+1. Взависимости от числа степеней свободы сис-мы дел-ся:инвариантные и конвариантные,(F=0),моновариантные(F=1)дивариантные(F=2),и т.д.При F=0 в равновесии нах-ся наибольшее число фаз для данной сис-мы. Термодин.степенью свободы системы наз-ся число термодин.параметров,которые можно независимо менять,не меняя при этом числа и вида фаз данной системы. В однокомпонентных системах фазы состоят из одного в-ва в различных агрегатных состояниях.Если в-во может давать различные крст-кие модиф-ции,то каждая из них яв-ся особой фазой. Диаграмма состояния однокомпонентной системы (Н2О при средних Р до 1МПа). 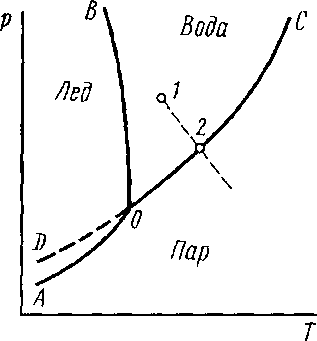 3 кривые разбивают диаграмму на поля,каждое из которых отвечает одному из агрегат.состояний воды-пару,жидкости или льду.Кривые отвечают равновесию между соот-щими 2-мя фазами. Кривая ОС хар-ет зависимость Р насыщ.пара жид.воды от Т и наз-ся кривой испарения;кривая ОВ-завис-ть Т замерзания воды от внеш.Р и наз-ся кривой плавления;кривая ОА-завис-ть плавления насыщ.пара льда от Т и наз-ся кривой возгонки.Точка О выр-ет условия одновременного равновесия между паром,льдом и жид. водой. 28)Равновесие чис-го в-ва в 2-х фазах одноком.сис-мы. Рассмотрим закономерности,связанные с превращением одной фазы чистого в-ва в другую.Сюда можно отнести плавление,испарение,кипение,возгонку и переход тв.тела из одной полиморфной модиф-ции в другую.На основе соотношения dG 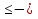 SdT SdT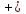 Vdp для обратимых процессов и ур-я dGp,T= Vdp для обратимых процессов и ур-я dGp,T=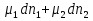 … или dGp,T=( … или dGp,T=(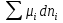 )p,T можно написать выр-я(1) для хим.потенциала (одного моля) чис-го в-ва в 1-ой и 2-ой фазах: )p,T можно написать выр-я(1) для хим.потенциала (одного моля) чис-го в-ва в 1-ой и 2-ой фазах: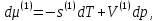 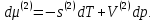 При равновесии между фазами выполняется условие 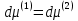 и из выр-ий (1) получ. выр-я(2) и из выр-ий (1) получ. выр-я(2) 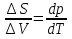 , , где 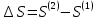 ; ;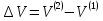 . .Для обратимых изотерм.переходов 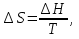 где где 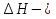 теплота фаз.перехода;T-тем-ра фаз.перехода.Подставляя значение теплота фаз.перехода;T-тем-ра фаз.перехода.Подставляя значение 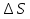 в выр-е (2) получ. выр-е (3): в выр-е (2) получ. выр-е (3):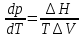 , наз. урав-е Клайперона-Клаузиуса . , наз. урав-е Клайперона-Клаузиуса .Для процессов испарения ур-е Клайперона Клаузиуса (3)удобно представить в др.виде.если рассматр.пар при внешних условиях (Т,р),то V данного кол-ва в-ва в парообразном состоянии знач-но больше его V в жид. состоянии,т.е. Vп 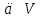 ж;поэтому приращение объёма (4) ж;поэтому приращение объёма (4) 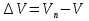 ж жможно считать прак-ки равным объёму пара и заменить 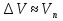 .Для моля идеал.газа или пара (5) .Для моля идеал.газа или пара (5)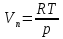 . .С учётом соотношений (4) и (5) ур-е (3) примет вид (6): 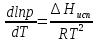 , где , где 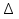 Hисп-молярная теплота испарения. Hисп-молярная теплота испарения.Поскольку 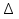 Hисп,R,T всегда положительны,производная Hисп,R,T всегда положительны,производная 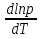 также всегда положительна,т.е. с ростом тем-ры давление насыщ.пара над жидкостью всегда увел-ся.В узком интервале тем-р можно принять приближённо величину также всегда положительна,т.е. с ростом тем-ры давление насыщ.пара над жидкостью всегда увел-ся.В узком интервале тем-р можно принять приближённо величину 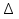 Hисп постоянной ;при этом интегрирование выражения (6)даёт lnp=C- Hисп постоянной ;при этом интегрирование выражения (6)даёт lnp=C-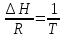 ,(7) где С-константа интегрирования.Из ур-я (7) видно что зависимость lnp от ,(7) где С-константа интегрирования.Из ур-я (7) видно что зависимость lnp от 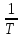 имеет линейный хар-р.по тангенсу угла наклона прямой на графике в коор-тах lnp- имеет линейный хар-р.по тангенсу угла наклона прямой на графике в коор-тах lnp-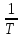 можно вычислить теплоту испарения (или сублимации). можно вычислить теплоту испарения (или сублимации).29) Определение теплоты спарение расчетным и графическим способами на основе уравнения Клаузиуса – Клапейрона. Химическая термодинамика раздел физической химии, рассматривающий термодинамические явления в области химии, а также зависимости термодинамических свойств веществ от их состава и агрегатного состояния. Т. х. тесно связана с термохимией, учением о равновесии химическом и учением о растворах (в частности, электролитов), теорией электродных потенциалов, с термодинамикой поверхностных явлений. Т. х. базируется на общих положениях и выводах термодинамики и прежде всего - на первом начале термодинамики и втором начале термодинамики. Первое начало и важнейшее его следствие - Гесса закон служат основой термохимии. При термохимических расчётах большую роль играют теплоты образования веществ, значения которых для каждого из реагентов позволяют легко вычислить тепловой эффект реакции; для органических веществ подобную роль играют теплоты сгорания. Наряду с измерениями тепловых эффектов различных процессов (см. Калориметрия) используются и определение энергии связи между атомами на основе спектральных данных, и различные приближённые закономерности. Первое начало термодинамики лежит в основе Кирхгофа уравнения, выражающего температурную зависимость теплового эффекта химической реакции. Второе начало термодинамики служит основой учения о равновесии, в частности химического. Его применение к изучению химических реакции впервые было дано в работах Дж. Гиббса, А. Л. Потылицына, Г. Гельмгольца, Я. Вант-Гоффа, А. Л. Ле Шателье. В Т. х. второе начало позволяет установить, как изменение внешних условий (например, температуры, давления) влияет на равновесие и, следовательно, какими они должны быть, чтобы рассматриваемый процесс мог совершаться самопроизвольно (то есть без затраты работы извне) в нужном направлении и с оптимальными результатами. В Т. х. для определения характеристик процесса применяют различные термодинамические функции. Наряду с энтропией S, изменением которой наиболее просто характеризуются процессы в изолированных системах, широко используют потенциалы термодинамические, позволяющие получить характеристики процессов при различных условиях их проведения Рассмотрим закономерности, связанные с превращением одной фазы чистого вещества в другую. Сюда можно отнести плавление, испарение, кипение, возгонку и переход твёрдого тела из одной полиморфной модификации в другую. Выражение dp/dT=ΔHф,п/TΔV называется ур-м Клапейрона-Клаузиуса. Для процессов испарения и сублимации: Если рассматривать пар при внешних условиях (Т,р), достаточно удалённых от критической точки, то объём данного кол-ва вещества в парообразном состоянии значительно больше его объёма в жидком состоянии, т.е.Vп>>Vж; поэтому приращение объёма можно считать практически равным объёму пара и заменить. Для моля идеального пара или газа Vп=RT/p. Dlnp/dT=ΔHисп/RT2, где ΔHисп– молярная теплота испарения. Поскольку ΔHисп,R,T всегда положительны, производная Dlnp/dT также всегда положительна, т.е. с ростом температуры давление насыщенного пара над жидкостью всегда увеличивается. В узком интервале температур можно принять приближенно величину ΔHисп постоянной; при этом интегрирование выражения даёт lnp=C - ΔHисп/R*1/T, где С- константа интегрирования. Из ур-я видно,что зависимость lnpот 1/T имеет линейный характер. По тангенсу угла наклона прямой на графике в координатах lnp – 1/T можно вычислить теплоту испарения( или сублимации) 30) Гетерогенное равновесие. Бинарные системы. Законы Рауля. Законы Коновалова. Обратимая реакция, протекающая в любой системе при постоянной температуре характеризуется наступлением состояния истинного химического равновесия. В этом состоянии выполняется (по определению) условие неизменности во времени молярных концентраций реагентов и продуктов, называемых равновесными концентрациями. В отличие от молярной концентрации некоторого вещества В (сВ) в любом неравновесном состоянии системы равновесная концентрация того же вещества обозначается квадратными скобками [В]. Для обратимой химической реакции, протекающей при некоторой температуре, устанавливаются любые, но постоянные равновесные концентрации [А], [В], [С], [D]. Они не зависят друг от друга, а определяются только положением состояния равновесия. В соответствии с законом действующих масс состояние равновесной химической системы характеризуется константой равновесия: Выражение (5.2) позволяет рассчитать KС по известным равновесным концентрациям всех веществ гомогенной газофазной реакции (5.1), а также для гомогенной реакции в растворе, например или концентрацию одного из веществ по известным равновесным концентрациям остальных веществ и KС. Первый закон Коновалова: пар над семью двух летучих жидкостей относительно богаче тем из компонентов, прибавление которого к смеси повышает общее давление пара при данной температуре или понижает температуру кипения смеси при данном давлении: X’2>X2 и X’1 X’2 Для летучих смесей первого типа увеличение содержания второго компонента в растворе повышает общее давление пара , так как производная dp/dx2 положительна. При этом содержание второго компонента в паре выше, чем в растворе. Для летучих смесей второго типа производная dp/dx2 положительна и содержание второго компонента в паре выше, чем в растворе. Второй закон Коновалова: экстремальные точки на кривой общее давление пара-состав раствора( или на кривой температура кипения –состав раствора) отвечают растворам , состав которых одинаков с составом равновесного с ним пара. Жидкая летучая смесь такого состава называется азеотропным: X’2=X2и X’1=X1. P1=p*1x1, p2=p*2x2, где p*1- давление пара над жидким растворителем;p*2- давление пара над (чистым) жидким растворенным веществом: Эти выражения называются законом Рауля или уравнениями Рауля. Равновесное парциальное давление пара компонента в идеальном растворе пропорционально молярной доле этого компонента в растворе. Зависимость парциального давления пара компонента от состава имеет вид прямой. Для твёрдого растворённого вещества p*2 в уравнении представляет собой давление насыщенного пара над переохлаждённой жидкостью при той же температуре. Уравнение Рауля позволяет установить зависимость давление пара над чистым твёрдым растворённым веществом от его растворимости в идеальном растворе. В насыщенном идеальном растворе парциальное давление пара растворённого вещества над раствором р2нас равно давлению насыщенного пара над твёрдым веществом р*2(т). при этом из ур-я Рауля получаем Р*2(т)=р*2(ж)х2нас , гдех2нас- растворимость вещ-ва в идеальном растворе, молярные доли. В предельно разбавленном растворе ур-е Рауля применимо к растворителю. По этому ур-ю можно определить молекулярную массу нелетучего растворенного вещества, если известно давление пара растворителя над разбавленным раствором : М2=М1 * g2/g1 * 1/(дельта p1/p*1), где М – молекулярная масса растворителя; g1- масса растворителя; g2- масса растворённого вещ-ва. К растворённому веществу в предельно разбавленном растворе формула Рауля не применима. 31) Основные понятия химической кинетики: скорость, механизм реакции. химическая кинетика- это учение о хим.процессе, его механизме и закономерностях протекания во времени. Хим.кинетика позволяет предсказывать скорость хим.процессов. для этого нужно знать механизм процесса, т.е. протекание сложных реакций по стадиям. Создание математической теории хим.процесса является в настоящее время необходимым условием для проектирования хим.реакторов. отсутствие таких сведений о механизме многих сложных реакций затрудняет предсказание их скорости и условий осуществления на практике. Хим.реакции являются сложными, т.е. протекают через ряд элементарных стадий. Элементарная стадия является наиболее простой составной частью сложной реакции: каждый акт элементарной стадии представляет собой рез-тат непосредственного взаимодействия и превращения нескольких частиц. Совокупность реакций из элементарных стадий называется механизмом реакции. При протекании реакции по стадиям получаются и расходуются промежуточные вещества. Промежуточными веществами обычно являются активные частицы с неспаренными электронами, так называемые радикалы. Сложные реакции могут состоять из двусторонних, параллельных и последовательных элементарных стадий. Скоростью образования (или изменения содержания данного i-того вещ-ва(компонента)) во время хим.реакции или, другими словами, скростью реакции w(i)по данному i-тому вещ-ву называется изменение кол-ва этого вещ-ваmi (в молях) в единицу времени t и в единице реакционного пространства R: w(i)=1/R*dmi/dt.Механизм реакции - это совокупность стадии, из которых состоит данный химический процесс. Установление механизма химической реакции - это сложный процесс. Полное описание механизма реакций включает решение нескольких задач:
|
