Шпоры по матану(1 курс). 1. Функция, одз

• Название: 1. Функция, одз
• Анкор: Шпоры по матану(1 курс).doc
• Дата: 25.03.2018
• Размер: 0.69 Mb.
• Имя файла: Шпоры по матану(1 курс).doc
• Тип: Документы; #17195
• страница: 11 из 33

2. Неопределенный интеграл и его св-ва.

Опр. Совокупность всех первообразных для ф-и f(x) на множестве наз. Неопределенным интегралом этой функции. ∫f(x)dx=F(x)+c, f(x)-подинтегральная ф-я ,f(x)dx – подинтегральное выражение.

Свойства.

1)[f(x)dx]’=f(x)

док-во: ∫f(x)dx=F(x)+c(по опр.), (∫f(x)dx)’= (F(x)+c)’=F’(x)=f(x)

2) d[f(x)dx] = f(x)dx

док-во: по опр. дифференциала: d[f(x)dx] = (f(x)dx)’dx=f(x)dx

3)∫dF(x)=F(x) +c

док-во: ∫dF(x)=∫F’(x)dx=∫f(x)dx=F(x)+c.

4)Постоянный множитель можно выносить за знак неопред. Интеграла:

∫kf(x)dx=k∫f(x)dx ,x є D, k є R.

док-во: покажем, что k∫f(x)dx – совокупность первообразных для ф-и k*f(x):

По св-ву производной: (k∫f(x)dx)’=k*(∫f(x)dx)’=k*f(x).

5)∫[f(x)+(-)g(x)]dx = ∫f(x)dx +(-)∫g(x)dx/

Док-во: докажем, что ∫f(x)dx +(-)∫g(x)dx – первообразная для ф-и [f(x)+(-)g(x)]:

По св-ву производной: [f(x)+(-)g(x)]’= [∫f(x)dx]’ +(-)[∫g(x)dx]’= f(x)+(-)g(x), что и т.д.

3 Табличные интегралы.

Таблица интегралов

1. 
   ∫ 0 dx = C = const 11) ∫dx/(√1-x² )= arcsin x + C = - arccos x + C
   
2. 
   ∫dx = x + C 12) ∫dx/(1+x²) = arctg x + C = - arcctg x + C
   
3. 
   ∫x^dx = x^+1/(+1) + C, 13) ∫tgxdx = - ln |cosx| + C
   

≠ -1 14) ∫ctgxdx = ln |sinx| + C

4. 
   ∫dx/x = ln|x| + C 15) ∫ dx/(√a²- x²)=arcsinx/a +C=-arccos x/a + C
   
5. 
   ∫e^xdx = e^x + C 16) ∫dx/(a²+x²) = (1/a)arctg x/a + C=-(1/a)arcctg x/a + C
   
6. 
   ∫a^xdx = a^x/lnx + C 17) ∫dx/(x²–a²) = (1/2a) ln |(x-a)/(x+a)| + C
   
7. 
   ∫cosx dx = sinx + C 18) ∫dx/(a²-x²) = (1/2a) ln |(x+a)/(x-a)| + C
   
8. 
   ∫sinxdx = - cosx + C 19) ∫dx/(√x²+A) = ln |x + (√x²+A)| + C
   
9. 
   ∫dx/cos²x = tgx + C
   

20) ∫(√x²+A)dx = (x/2)(√x²+A) + (A/2) ln |x+(√x²+A)|+C

10. 
    ∫dx/sin²x = - ctgx + C
    

21) ∫ (√a²- x²)dx = (a²/2) arcsin x/a + (x/2) (√a²- x²) + C

4. Метод замены переменной или метод подстановки

∫f(x)dx, x  D

Пусть x = φ(t), t  T, φ(t) – дифференцируема на T и имеет обратную функцию

Докажем, что ∫ f(x)dx = ∫f(φ(t)) • φ’(t)dt, т. е. докажем, что ∫f(x)dx – первообразная f(φ(t))•φ’(t)

(∫f(x)dx)_t’(по правилу дифференцирования сложной функции) = (∫f(x)dx)_x’ • x’_t = f(x)•φ’(t) = f(φ(t))•φ’(t)

∫ f(x)dx = ∫f(φ(t)) • φ’(t)dt – формула замены переменной в неопределенном интеграле

5. Метод интегрирования по частям

Пусть u = u(x), v = v(x) – дифференцируемы на D

d(u•v) = du•v + u•dv  ∫ d(u•v) = ∫du•v + ∫u•dv  u•v = ∫v•du + ∫u•dv 

∫u•dv = u•v - ∫v•du – формула интегрирования по частям

Применение данной формулы:

1. P_n (x)•φ(x)dx; P_n (x) – многочлен n-ой степени

а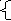) φ(x) = sin ax u = P_n (x); dv = φ(x)dx

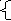cos ax

e^Kx

b) φ(x) = обратные тригонометрические функции u = φ(x); dv = P_n (x)dx

log_ax
2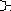. e^kx•sin ax dx в этом случае любой из множителей можно принять

e^kx•cos ax dx за u

5. Интегрирование рациональных дробей. Интегрирование некоторых классов иррациональных и трансцендентных функций.

(конкретные числовые примеры по данному вопросу см. в лекции за 21.03.00)

Рассмотрим интегал вида R(x)dx, где R(x) – рациональная функция, т.е функция, которую можно представить в виде отношения двух многочленов R(x)=P(x)/Q(x). Если эта дробь неправильная, то можно выполнить деление с остатком и представить R(x) в виде суммы некоторого многочлена и правильной дроби.

Теорема. Всякая правильная дробь может быть представлена как сумма простейших дробей вида

A ; A ; Mx+N ; Mx+N .

x-a (x-a)ⁿ x²+px+q (x²+px+q)ⁿ

, где A,M,N,a,p,q – действительные числа.

Непростейшие дроби.

Лемма 1. Пусть F(x)/Q(x) – правильная дробь. Если х=а- корень Q(x) кратности К,т.е. Q(x)=(x-a)^K_*Q₁(x), где Q₁(a) не равно нулю, то F(x)= A_K+ F₁(x)

Q(x) (x-a)^K Q₁(x)_*(x-a)^K-1

Лемма 2. Пусть F(x)/Q(x) – правильная дробь. Если Q(x)=(x²+px+q)^K_*Q₁(x) 

F(x) =M_Kx+N_K+ F₁(x) .

Q(x) (x²+px+q)^K (x²+px+q)^K-1_*Q₁(x)

Теорема разложения правилоной дроби на простейшие. Пусть F(x)/Q(x) – правильная дробь. Если Q(x)=(x-a)^(x-b)^_*…_*(x-c)^(x²+p₁x+q₁)^K_*…_*(x²+p₂x+q₂)^m  эта дробь разлагается в сумму простейших дробей следующего вида:

F(x) = A_+ A_-1+…+ A₁+ B_+ B_-1+…+ B₁+ C_+ C_-1+…+ C₁+

Q(x) (x-a)^ (x-a) ^-1 x-a (x-b)^ (x-b) ^-1 x-b (x-c)^ (x-c) ^-1 x-c

+ M_Kx+N_K + M_K-1x+N_K-1+…+ M₁x+N₁+ C_mx+D_m + C_m-1x+D_m-1+…+ C₁x+D₁

(x²+p₁x+q₁)^K (x²+p₁x+q₁)^K-1 x²+p₁x+q₁ (x²+p₂x+q₂)^m (x²+p₂x+q₂)^m-1 x²+p₂x+q₂

Интегрирование иррациональных и трансцендентных функций.

Трансцендентная функция – аналитическая функция, не являющаяся алгебраической. (Например, показательная функция тригонометрической функции.)

R(x,x^m1/n1,…x^mk/nk)dx, где R – рациональная функция от х и её дробных степеней. Такой интеграл может быть решён с помощью замены степени с дробным показателем на степень функции с целым показателем. (подробнее см. в лекциях)

.

R(x,Ax²+Bx+C )dx Под корнем выделяется полный квадрат и решается с помощью замены переменной.

. .

dx/ Ax²+Bx+C ,  Ax²+Bx+C dx