1. Харка методики фэмп у дошкольников как науки и учебной дисциплины. Мфэмп

• Название: 1. Харка методики фэмп у дошкольников как науки и учебной дисциплины. Мфэмп
• Дата: 01.03.2018
• Размер: 255.51 Kb.
• Имя файла: FEMP.docx
• Тип: Документы; #37549
• страница: 2 из 12

11.Соврем. концепции предматем. подготовки дош-в в трудах отечеств. исследователей.

Психологи в качестве основания для ФЭМП и понятий предлагали различные предметные действия. П.Я. Гальперин разработал линию форм-ия начальных матем. понятий и действий, построенную на введении мерки и определении единицы через отношение к мерке. Число при таком подходе воспринималось р-ом как результат измерения, как отношение измеряемой величины к избранной мерке. На основе этих и др.исследований в программу об-ия д-й была включена тема «Освоение величин».

В исследовании В.В. Давыдовабыл раскрыт психол-ий механизм счета, как умственной деят-ти и намечены пути форм-ия понятия числа через освоение д-ми действий уравнивания, комплектования и измерения.

Анализ содержания об-ия дошк-ов с точки зрения новых задач привел исследователей к выводу о необходимости учить д-й обобщенным способам решения познав-ых задач, усвоению связей, зависимостей, отношений и логических операций (классификации и сериации).

Методику первонач. об-ия А.И. Маркушевич рекомендовал строить, основываясь на положениях теории множеств. Он считал необходимым об-ть дошк-ов простейшим операциям с множествами, разв. у них количе-ные и простр-ные представл.

В пед. исследованиях выяснялись возможности разв. у д-й представл. о величине, установления взаимосвязей между счетом и измерением; апробировались приемы об-ия (Р.Л. Березина, Н.Г. Белоус, 3.Е. Лебедева, Р.Л. Непомнящая, Е.В. Проскура, Л.А. Левинова, Т.В. Тарунтаева, Е.И. Щербакова).

Возможности форм-ия колич-ных представлений у д-й р\в и пути их совершенствования у дошк-ов изучены В.В. Даниловой, Л.И. Ермолаевой, Е.А. Тархановой.

Содержание и приемы освоения пространственно-временных отношений определены на основе исследований Т.А. Мусейибовой, К.В. Назаренко, Т.Д. Рихтерман. Методы и приемы матем. развития д-й, с помощью игры были разработаны З.А. Грачевой (Михайловой), Т.Н. Игнатовой, А.А. Смоленцевой, И.И. Щербининой.

Исследовались возможности использования наглядного моделирования, в процессе об-ия решению арифметических задач (Н.И. Непомнящая), познания детьми колич. и функцион. зависимостей (Л.Н. Бондаренко, Р.Л. Непомнящая, А.И. Кириллова), сп-сти дошк-ов к наглядному моделированию, при освоении пространственных отношений (Р.И. Говорова, О. М. Дьяченко, Т.В. Лаврентьева, Л.М. Хализева).

Т. о, на протяжении последних лет методика пополнилась теоретическими исследованиями в разных конкретных направлениях, что значительно повысило общеразвивающий эффект об-ия. Однако в теории и практике дош-го восп-ия есть еще ряд нерешенных проблем.

Одной из актуальных проблем МФЭМП явл. проблема преемственности в работе д\с и школы, а в связи с этим дальнейшая разработка эффективных м-ов и приемов об-ия. Изучение математики в начальной школе предусматривает достаточно широкую и глубокую ориентацию д-й в колич-ных и простр-ных отношениях окружающей действительности. Соврем.об-ие в д\с не всегда в полной мере решает эти задачи. Нередко математические знания дети усваивают формально, без должного их понимания. Одной из причин такого уровня знаний явл. недостаточная разработка отдельных методических вопросов. Так, современное об-ние математике в д\с во многом ориентируется на вербальные (словесные) м-ы, кот.дают возможность форм-ть у д-й конкретные ЗУН, и недостаточно ориентируется на м-ды, кот. содействуют развитию у них познавательных интересов и сп-тей, логического мышления.

12.Соврем. концепции предматемат. подготовки дошк-ков в трудах зарубежных пед-в и психологов.

Ж. Папи (бельгийский математик) разработал интересную методику форм-ия у д-й представлений об отношениях, функциях, отображении, порядке и др., с использованием многоцветных графов.

М. Фидлер (Польша), Э. Дум, Д. Альтхауз (Германия) особое значение придавали разв. представ. о числах в процессе практических действий с множествами предметов. Предлагаемые ими содержание и приемы об-ия (целенаправленные игры и упражнения) помогали д-м овладеть умениями классифицировать и упорядочивать предметы по различным признакам, в том числе и по количеству.

Р. Грин и В. Лаксон (США) в качестве основы разв. понятия числа и арифметических действий рассматривали понимание д-ми колич-ных отношений на конкретных множествах предметов. Авторы уделяли большое внимание познанию д-ми принципа сохранения количества в процессе практич. действий по преобразованию дискретных и непрерывных величин.

Содержание математ-го развития в материнских школах Франции было направлено на освоение детьми классификации, отношений сходства, формирование понятий пространства и времени (по материалам Т.Я. Миндлиной). Уделялось большое внимание счету. Причем, по мнению французских специалистов, дети до 4 лет должны были учиться считать без вмешательства взрослого. Играя с водой, песком и прочими веществами, малыши осваивали понятия о количестве и величине на сенсорном уровне, для д-й старше 4 лет рекомендовались систематические упраж-я, направленные на формирование представл. о числах.

Французские педагоги материнских школ считали, что сп-сть к математике зависит от качества об-ия. Ими была разработана система логических игр для д-й разного возраста. В процессе игры у д-й развивались сп-сть к рассуждению, пониманию, самоконтролю, умение переносить усвоенное в новые ситуации. Дети 5-6 лет осваивали элементарные математ. понятия, в том числе понятие множества, используя математ. язык; учились точно и кратко выражать свои мысли, обнаруживать и исправлять ошибки, допущенные другим ребенком.

13.Совр подходы к реализации пед. принципов отбора содерж. и орган процесса ФЭМП у д. д\в.

В наст. время благодаря усилиям ученых и практиков создана, успешно функционирует и соверш-ется научно обоснованная методич. система по ФЭМП у дошк-ов.

Линейно-концентрический принцип, кот. лежит в основе ФЭМП, предполагает в каждом возрастном этапе повторение на более высоком уровне того, что было освоено на предыдущей ступени, и дальнейшее продвижение вперед. Однако в каждом году об-ия выделяется одно главное направление. Во 2 мл. гр. – формир. представл. о равенстве и неравенстве групп по количеству входящих в них предметов, в ср. гр.– формир. представл. о числах в пределах 5, в ст. – формир. представл. о числах и отношениях между последовательными числами в пределах 10.

Критерии отбора содерж. математ. разв. дош-в:

1.Личностно-развивающая направленность содерж. математ. разв. дошк-в. Оно должно являться эффек. ср-ом разв. его интеллек-но-творческих сп-тей и содейст-ть разв. самост-сти в решении интеллек-ых задач.

2.Социализирующая направл-сть на опред-ый логико-математ. опыт р-ка станет его значимым личностным приобретением, если обеспечит ситуацию успеха.

3.Индив-ный подход осущ-ется при соответствии содержания материала возможностям р-ка и на занятиях, и в индив-ной работе.

4.При личностно-ориентированном подходе необход. учитывать тип темперамента р-ка; матем. разв. д\б соразмерено возрастным и индивид. сп-тям д-й; р-к – центральная фигура в процессе об-ия, с его возможностями, желаниями, интересами.

5.Необходима ориентация на зону ближ. разв.: давать знания немного труднее, чем р-к может усвоить без усилий, чтобы была необход. активиз-ть мыслит. деят.

В учебной программе задачи по матем. разв. направлена на формир. у р-ка представл. о том, что окруж. мир имеет математ. характ-ки. Освоение матем. представлений, ЗУН происходит в различных видах деят-ти, в том числе и учебной. В д\в дети овладевают сравнением множеств практическим путем (наложение, приложение, графический способ) и опосредовано – через число; знакомятся с элементами знаковой системы; форм-ся представл. о числе как результате измерения. Углубляются и расшир. знания о геометр. фигурах и форме предметов; соверш. сп-сти ориентировки в простр. и времени.

Играя и занимаясь с д-ми, восп-ль способствует развитию у них умений и способностей:

-оперировать свойствами, отношениями объектов, числами; выявлять простейшие изменения и зависимости объектов по форме, величине;

-сравнивать, обобщать группы предметов, соотносить, вычленять закономерности чередования и следования, оперировать в плане представлений, стремиться к творчеству;

-проявлять инициативу в деят-сти, самост-сть в уточнении или выдвижении цели, в ходе рассуждений, в выполнении и достижении результата;

-рассказывать о выполняемом или выполненном действии, разговаривать со взрослыми, сверстниками по поводу содержания игрового (практического) действия.

Пятилетки проявляют высокую познавательную активность, они буквально забрасывают старших разнообразными вопросами об окружающем мире. Исследуя предметы, их свойства и качества, дети пользуются разнообразными обследовательскими действиями: умеют группировать объекты по цвету, форме, величине, назначению, количеству; умеют составить целое из 4-6 частей; осваивают счет.

Широкое использование устного народного творчества так же важно для пробуждения у дошк-ов интереса к математ. знаниям, совершенствования познав-ной деят-сти, общего умственного развития.

14.Понятия. Отнош. Логич. операции. и дедукт. выв.

Понятие – отображенное в мышлении единство существенных св-в, связей и отношений предметов или явлений; мысль или система мыслей, выделяющая и обобщающая предметы некоторого класса по определенным общим, и в совокупности специфических для них признакам.

Понятие не только выделяет общее, но и расчленяет предметы, их св-ва и отношения, классифицируя последние в соответствии с их различиями. Так, понятие «ч-к» отражает и существенно общее (то, что свойственно всем людям), и отличие любого ч-ка от всего прочего.

Отношение – философская категория или научный термин, обозначающий любое понятие, реальным коррелятом кот. является определенное соотнесение (связь) двух и более предметов.

В математике отношение – результат деления одной величины на другую.

Отношение – обобщение арифметических отношений, таких как «=» и «<».

Отношение в логике первого порядка – двух- и более аргументный предикат (многоместный предикат), двух- и более предикатное свойство. Знак отношения – R.

В логике логическими операциями называют действия, вследствие кот. порождаются новые понятия, возможно с использованием уже существующих. В более узком, формализованном смысле, понятие логические операции использ. в математ. логике и программировании.

Логические операции с понятиями – такие мыслительные действия, результатом кот. явл. изменение содержания или объема понятий, а также образование новых понятий.

К операциям, кот. связаны преимущественно с изменением содержания понятий, относятся: отрицание, ограничение, обобщение, деление. К операциям, которые связаны преимущественно с объемами понятий, относятся: сложение, умножение, вычитание. Данные операции м\ б записаны математически, с помощью теории множеств. Переход же к математ-ой логике связан с понятием суждений и установлением операций над ними с целью получения сложных суждений.

Индукция – процесс логического вывода, на основе перехода от частного положения к общему. Индуктивный вывод – вывод от фактов к цели. Индуктивное умозаключение связывает частные предпосылки с заключением не строго через законы логики, а скорее через некоторые фактические, психолог-ие или математ. представл. Объективным основанием индуктивн. умозакл. явл. всеобщая связь явлений в природе.

Различ. полную индукцию – метод доказательства, при кот. утверждение доказывается для конечного числа частных случаев, исчерпывающих все возможности, и неполную индукцию – наблюдения за отдельными частными случаями наводят на гипотезу, кот., конечно, нуждается в доказательстве. Также для доказательств используется м-д математической индукции.

Дедукция – м-д мышления, при кот. частное положение логическим путем выводится из общего, вывод по правилам логики; цепь умозакл-ий (рассуждений), звенья кот. (высказывания) связаны отношением логич. следования.Дедукт. вывод представляет собой цепь утверждений, каждое из кот. есть или посылка, или утверждение, непосредственно следующее по законам логики из утверждений, уже имевших место в этой цепи. Началом (посылками) дедукции явл.аксиомы или просто гипотезы, имеющие характер общих утверждений («общее»), а концом – следствия из посылок, теоремы («частное»). Если посылки дедукции истинны, то истинны и ее следствия. Дедукция – основное ср-во доказательства. Противоположно индукции.

15.Множество. Виды множеств. Элемент множества. Подмножество.

В математике основн понятием явл. понятие множества.

Множество– совокупность объектов, объединенных по какому – либо признаку и воспринимаемых как единое целое. Под характеристическим свойством множества понимаю такое свойсто,кот. обладают все предметы, принадлежащие этому множеству (элементы этого множества),и не обладает ни один предмет, не принадлежащий ему(не являющимся его элементом).

Виды множеств:

конечное- элементы кот. можно пересчитать (множество пальцев).

бесконечное –элементы кот. нельзя исчерпать отнимая по одному элементу.

пустое-множество,кот. не удерживает в себе ни одного элемента.

единое-множество, кот.удерживает в себе только один элемент.

Равные множества – это два или более множеств, состоящих из равных наборов элементов. Приведем пример. Скажем, все члены Вашей семьи находятся на кухне. Т. о, Множество «Члены семьи на кухне» будет равно множеству «Члены семьи в квартире». Если два множества – А и B – состоят из одинакового набора элементов, то они будут равны, то есть, А=B. Элементы множеств могут перечисляться в любой последовательности, на результат это никак не влияет.

Универсальное множество – множество, содержащее все объекты и все множества. В тех аксиоматиках, в кот. универсальное множество сущ., оно единственно.

Множества состоят из элементов. Элементами множества называют объекты, составляющие множества. Это м\б реальные предметы (вещи, игрушки, рисунки), а также звуки, движения, числа и др.

Элементами множества м\б не только отдельные объекты, но и их совокупности. Например, при счете парами, тройками, десятками. В этих случаях элементами множества выступает не один предмет, а два, три, десять - совокупность.

Т.о, множества рассматривают как набор, совокупность, собрание каких-либо предметов и объектов, объединённых общим, для всех характерным свойством.

Подмножество – это часть множества, входящее в данное множество. Каждое непустое множество имеет по крайней мере два подмножества: 1) пустое множество является подмножеством любого множества; 2) каждое множество является подмножеством самого себя.

16. Операции над множествами.

1.объединение-множество, кот. состоит из элементов принадлежащему к одному из заданных множеств.

2.пересичение-элементы принадлежат одновременно и одному и другому множеству( общие элементы)

3.удаление-множество элементы которого принадлежат одному множеству, но не принадлежат другому.

4.дополнение к подмножеству- множество в которое входят элементы заданного множества, но не входят элементы заданного подмножества.

Два множества А и В равны (А=В), если они состоят из одних и тех же элементов. Например, если А={1,2,3,4}, B={3,1,4,2} то А=В.

Объединением (суммой) множеств А и В называется множество А ∪ В, элементы кот.принадлежат хотя бы одному из этих множеств. Например, если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6}

Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы кот.принадлежат как множеству А, так и множеству В. Например, если А={1,2,4}, B={3,4,5,2}, то А ∩ В = {2,4}

Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А, но не принадлежат множеству В. Например, если А={1,2,3,4}, B={3,4,5}, то АВ = {1,2}

Симметричной разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств АВ и ВА, то есть А Δ В = (АВ) ∪ (ВА). Например, если А={1,2,3,4}, B={3,4,5,6}, то А Δ В = {1,2} ∪ {5,6} = {1,2,5,6}

Множества изображаются на плоскости с помощью кругов Эйлера.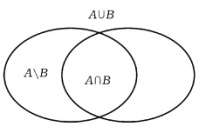

17.Число и цифра. История развития понятия числа и деятельности счета в филогенезе.

Число – основное понятие математики, используемое для количественной характер-ки, сравнения, нумерации объектов и их частей. Письменными знаками для обозначения чисел служат цифры, а также символы мат. операций.

Цифры – это система знаков («буквы») для записи чисел («слов») (числовые знаки). Слово «цифра» без уточнения обычно означает один из следующих десяти («алфавит») знаков: 0 1 2 3 4 5 6 7 8 9 (т.н. «арабские цифры»). 

Понятие о числе зародилось в глубокой древности, когда ч-к научился считать предметы: два дерева, семь быков, пять рыб. Сначала счет вели на пальцах. Позднее вместо пальцев для счета начали использовать зарубки на палочках. А когда возникла письменность, для обозначения чисел стали употреблять буквы. Постепенно люди стали осознавать числа независимо от предметов и лиц, кот/ могли подвергаться счету: просто число «два» или число «семь». В связи с этим у славян появилось слово число. В значении «счет, величина, количество» его начали употреблять в русском языке с ХI века. Наши предки использовали словочисло и для указания на дату, год. С XIII в. оно стало обозначать еще и дань, подать.

Можно выделить следующие этапы исторического развития числа: