Новая методичка статистика. 1 Расчёт основных статистических показателей для выборочных совокупностей
 Скачать 1.22 Mb. Скачать 1.22 Mb.
|
|
ВВЕДЕНИЕ Эффективность ведения современного лесного хозяйства определяется полнотой научных сведений, как о естественном формировании лесных фитоценозов, так и под воздействием хозяйственных мероприятий. Достоверность этих сведений оценивается путем статистической обработки цифрового материала, полученного в результате целенаправленно спланированного эксперимента и последующей производственной проверки. Каждый из существующих статистических методов имеет свои возможности и ограниченную область применения, продиктованную спецификой эксперимента. При этом все они служат экспериментатору средством выявления закономерностей, позволяющих сделать выводы и заключения в условиях неопределенности. Достоверно полученные результаты наблюдений, представление выявленных закономерностей в виде статистических моделей следует рассматривать в практическом приложении в качестве основы применения количественных методов моделирования и оптимизации экономических, технологических и других процессов, и явлений. 1 Расчёт основных статистических показателей для выборочных совокупностей Сбор необходимых материалов по изучению интересующих признаков должны осуществляться по чётко разработанной методике и программе. Объектом наблюдения служат биологические явления природы в их росте, развитии и во взаимной связи и зависимости друг с другом. Отдельные единицы (элементы) наблюдения – это варианты. Единицами наблюдения могут быть отдельные деревья, насаждение, древостой, пробная площадка, лента и т.д. Сумма единиц наблюдения (вариант) образует совокупность. По своим численным значениям варианты одной совокупности могут совпадать друг с другом, а могут и существенно различаться, равно как и сами совокупности. Каждая единица совокупности характеризуется признаками или качественными особенностями, которые могут быть одинаковыми (устойчивыми) для всех единиц (общие признаки), либо (изменчивыми) различными (варьирующие признаки). Изучаемые признаки у объектов наблюдений обладают той или иной степенью (мерой) изменчивости (вариабельности). Совокупность может быть генеральной и выборочной. Генеральная совокупность – это все единицы изучаемого объекта. Выборочная (выборка) – это часть единиц (вариант) отобранных из генеральной. По выборке можно сделать заключение о генеральной совокупности. Чем большим объёмом представлена выборка, тем точнее она будет характеризовать генеральные параметры. 1. 1 Малая выборочная совокупность Малая выборочная совокупность – это совокупность (выборка), объемом до 30 вариант. Данные малой выборочной совокупности обрабатываются без предварительной группировки всех единиц совокупности. Далее приводится полная характеристика изучаемого объекта. Например: Изучаемый объект – сосновый древостой Изучаемый признак – диаметр дерева на высоте 1,3 м Способ формирования выборочной совокупности - случайный Объём совокупности – 30 деревьев Данные обмера диаметров сосны на высоте 1,3 м приведены в таблице 1.1. Таблица 1.1 – Экспериментальные данные исследуемого объекта (соснового древостоя)
совокупности Средняя величина (арифметическая) – наиболее представительная характеристика распределения, это центр распределения изучаемого признака: где x1 ,x2 ,x3 ,xn – каждое значение варианты совокупности; n – объем выборочной совокупности. Например: Сумма квадратов отклонений (СКО) – сумма отклонений каждой варианты от средней величины (от центра распределения совокупности): где xi – каждое значение варианты совокупности; Например: СКО = (36,50-31,08)2+(29,00-31,08)2+ (27,50-31,08) 2 +(37,00-31,08)2+(36,00-31,08)2+…+(33,00-31,08)2=632,04 см 2 Дисперсия – это средний квадрат отклонений всех вариант совокупности от средней величины. Дисперсия характеризует степень разнообразия (изменчивости) объекта: Например: Стандартное отклонение (среднее квадратическое отклонение) – основной показатель вариации, характеризующий варьирование значений признака вокруг центра распределения. Среднее квадратичное отклонение является мерой надёжности средней величины. Чем меньше его численное значение, тем лучше средняя арифметическая отражает собой всю статистическую совокупность. Например: Коэффициент вариации – показатель меры изменчивости изучаемого признака (среднее квадратическое отклонение), выражающий ее в относительных единицах (то есть в процентах). Он представляет собой средний процент отклонения вариант от их среднего значения. Коэффициент вариации является наиболее распространенным показателем, используемым для оценки типичности средних величин. Данная характеристика не зависит от принятых единиц измерения, и поэтому может применяться для сравнительной оценки величины варьирования различных признаков, как в пределах одной совокупности, так и в разных совокупностях. Вместе с тем он в значительной степени зависит от средней величины, и поэтому его применяют ограниченно случаями, когда имеет место естественное (от нуля) начало отсчета или сходные начала отсчета: Например: Cv = 4,67×100 = 15,03 % 31,08 По величине расчётного коэффициента вариации определяется уровень изменчивости признака с помощью шкалы Мамаева представленной в таблице 1.2. Таблица 1.2 Шкала Мамаева для установления уровня изменчивости признака
Например: Расчётный коэффициент вариации Сv = 15,03 % тогда уровень изменчивости диаметра дерева на высоте 1,3 м низкий, т. к. коэффициент вариации находится в пределах от 7 до 15 %. Коэффициент дифференциации – характеризует изменчивость признака, выражая ее в относительных единицах. Смысл данного показателя такой же, как и у коэффициента вариации, но он устраняет его ограничения: где xmin– минимальное значение варианты изучаемого признака в совокупности. Степень дифференциации признака определяется по величине коэффициента дифференциации с помощью таблицы 1.3. Таблица 1.3 Классификация степени дифференциации признака
Например: Vd = 4,67×100 =65,96 % (31,08 – 24,00) Степень дифференциации большая, т. к. коэффициент дифференциации находится в пределах от 54 до 70 %. Ошибки репрезентативности (представительности) В результате изменчивости (варьирования) изучаемого признака, между статистическими показателями выборочной совокупности и генеральной, могут наблюдаться некоторые расхождения, которые являются случайными ошибками выборки и называют основными ошибками репрезентативности того или иного статистического показателя. Ошибка средней величины: Например: Ошибка стандартного отклонения: Например: Ошибка коэффициента вариации: Например: Ошибка точности: Например: Точность опыта (относительная ошибка опыта) Показатель точности опыта выражает величину ошибки средней величины в процентах от самой средней. Точность опыта или процент ошибки наблюдения – это процент расхождения между генеральной и выборочной средней. Чем меньше показатель процента ошибки, тем точность опыта выше. Точность опыта считается удовлетворительной, если численное значение данного показателя не превышает 5 %. Если показатель точности больше 5 % , то рекомендуется увеличить число наблюдений или число повторностей. Точность опыта можно повысить (численное значение соответственно снизить) путём повышения точности измерений объектов опыта. Например: Достоверность статистических показателей (надежность) Достоверность – это то, что не может вызвать сомнение. Степень надёжности статистического показателя – это достоверность. Оценку надёжности производят по t – критерию Стьюдента, который определяется как частное от деления величины статистического показателя к его ошибке репрезентативности. Это отношение должно быть ≥ 3. Если расчётное значение критерия равно или больше трёх, то значение статистического показателя достоверно и его можно использовать для сопоставлений и выводов. Если же расчётное значение критерия меньше трёх, то данный показатель можно считать ненадёжным, величина его не достоверна и она в той или иной мере вероятна. Достоверность средней величины: Например: Достоверность стандартного отклонения: Например: Достоверность коэффициента вариации: Например: Достоверность точности: Например: Доверительный интервал для генеральной средней ДИГС – интервал нахождения средней величины для всей генеральной совокупности. Чем меньше расстояние между точками интервала, тем точнее выборочная совокупность характеризует генеральные параметры. где t05 – критерий Стьюдента на 5% уровне значимости, определяется по числу степеней свободы (из приложения учебника). Число степеней свободы – это число свободно варьирующих вариант (k) k = n – 1 Для приведённого примера k = 30 – 1=29. Тогда в соответствии с найденным числом степеней свободы 29 теоретическое значение критерия Стьюдента будет равно t05 = 2,045. Далее производим расчёт ДИГС. Например: ДИГС 31,08 ± 0,85 × 2,045; ДИГС 29,34 ÷ 32,82 мм. Необходимое число наблюдений для будущих исследований В исследованиях можно встретить случаи, когда изучаемая совокупность имеет неизвестную численность. Тогда достаточный объём выборки из такой совокупности можно определить по формуле: где Cv– расчетный коэффициент вариации; p – заданная точность(в курсовой работе точность принять 2 %); К – коэффициент порогового уровня доверительной вероятности (К1=1,00; К2=1,98; К3=2,63) Например: Cv =15,03 %; p = 2 %;К1=1,00; К2=1,98; К3=2,63 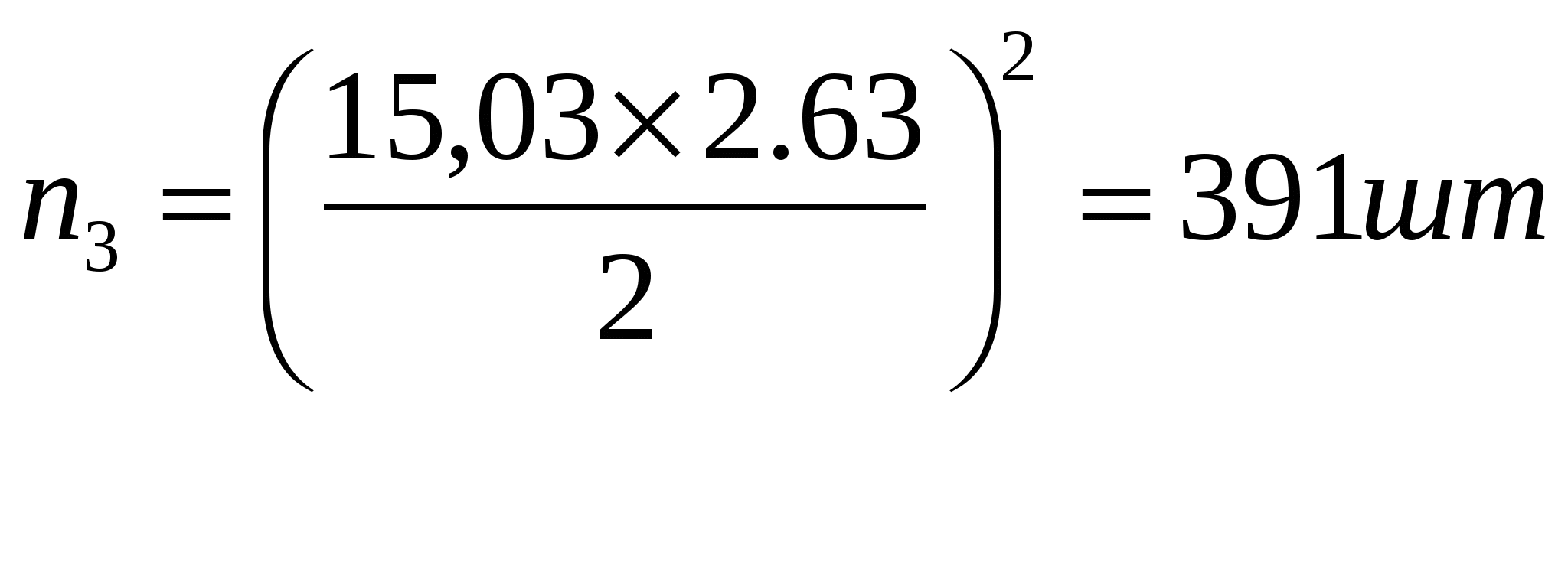 В курсовой работе рассчитать необходимое число наблюдений для будущих исследований для всех трёх пороговых уровней доверительной вероятности. |
