Новая методичка статистика. 1 Расчёт основных статистических показателей для выборочных совокупностей
 Скачать 1.22 Mb.
|
|
Мода (Мо или  ) – наиболее часто встречаемая варианта в эмпирической совокупности. Класс с наибольшей частотой называется модальным. Например, имеется следующий рад распределения деревьев по ступеням толщины (по диаметрам):Класс I II III IV V VI VII VIII IX X Групповая варианта (хi) 8 12 16 20 24 28 32 36 40 44 Частота класса (ni) 2 4 11 16 30 14 10 8 3 2 Наибольшее количество вариантов находится в V классе – 30 штук. Следовательно V класс – модальный. Соответственно варианта, которая наиболее часто встречается в данной выборочной совокупности, равна 24 см. Она же будет модой. = 24 см.Для определения моды можно использовать формулу: 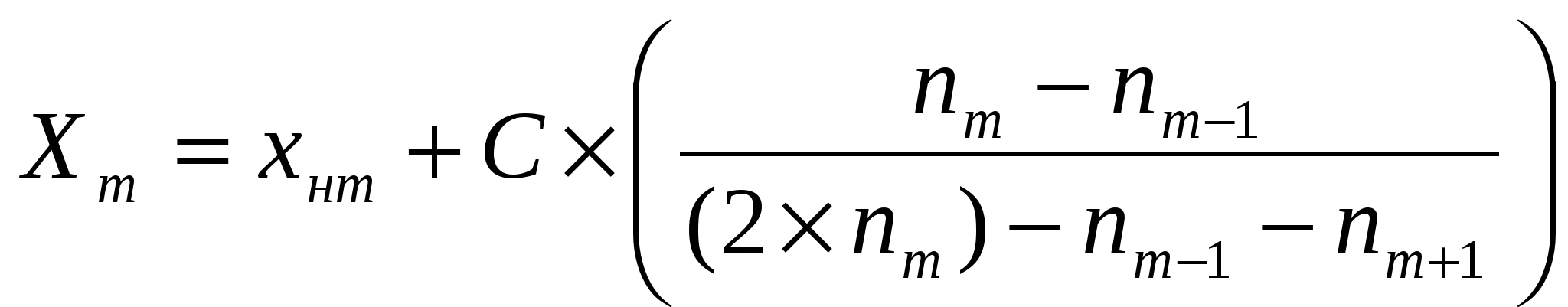 , где хнm– нижняя граница модального класса (22 см) С – классовый интервал (4 см) nm– частота модального класса, т.е класса с наибольшей частотой (30 шт) nm-1 –частота класса, предшествующего модальному (16 шт) nm+1 – частота следующего за модальным класса (14 шт) Тогда для приведённого ряда распределения мода численно будет равна:  Медиана (  или  )– это значение признака относительно, которого ряд распределения делится на две равные по численности части. Медиана – это варианта ряда которая занимает срединное в нём положение и делящая всю совокупность на две равные половины. Для небольших выборок определяется довольно просто. Для этого варианты выборки выстраивают в порядке возрастания и если число вариантов нечётное, то центральная варианта и будет его медианой. Например имеем ряд чисел: Групповая варианта (хi) 8 12 16 20 24 28 32 36 40 Тогда медиана будет равна 24 см, т.к она занимает срединное положение, по обе стороны от неё расположено по 4 варианты. = 24 см.При чётном числе вариантов медиана определяется по полусумме двух соседних вариант, расположенных в центре ряда. Например по большой выборочной совокупности медиана будет равна: Групповая варианта (хi) 8 12 16 20 24 28 32 36 40 44 = (24+28)/2 = 26 см.Если варианты выборочной совокупности сгруппированы в вариационный ряд, то медиану можно определить следующим образом. Сначала необходимо произвести накопление частот от класса к классу, при этом варианты ряда должны быть выстроены в порядке возрастания (т.е от меньшего к большему). Например: Класс I II III IV V VI VII VIII IX X Границы классов 6 - 10 – 14 – 18 – 22 – 26 – 30 – 34 – 38 – 42 - 46 Групповая варианта (хi) 8 12 16 20 24 28 32 36 40 44 Частота класса (ni) 2 4 11 16 30 14 10 8 3 2 Накопленная частота (Σni) 2 6 17 33 63 77 87 95 98 100 Далее медиана определяется по формул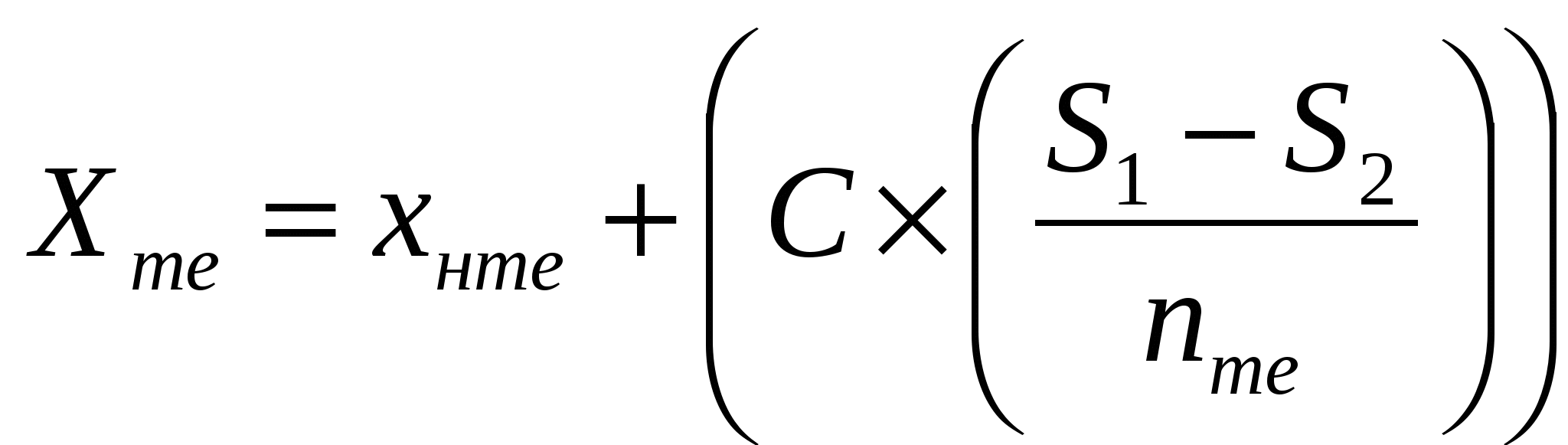е:  , гдехнme –значение нижней границы класса в котором находится медиана или класса в котором содержится половина накопленных частот (22 см, т.к N/2 = 100/2 = 50 шт. находится в V классе) C – величина классового интервала (4 см) S1 – полусумма общей численности ряда (N/2 = 100/2 = 50 шт.) S2 – число накопленных частот класса, предшествующего классу с медианой (33 шт.) nme – частота того класса в котором находится медиана ( 30 шт.)   Медиана может быть определена и графическим путём по кумуляте. Для этого на оси ординат отмечают точку, соответствующую половине накопленных частот ряда распределения. Затем из этой точки восстанавливают перпендикуляр дог пресечения с кумулятой. Опущенный из точки пересечения на ось абсцисс перпендикуляр указывает значение медианы. Например: полусумма накопленных частот рада распределения равна 50 шт. Отметив точку на оси ординат равную 50, проводим перпендикуляр до пересечения с кумулятой и опустив второй перпендикуляр из этой точки на ось абсцисс получаем, что численное значение медианы равно 24 см. 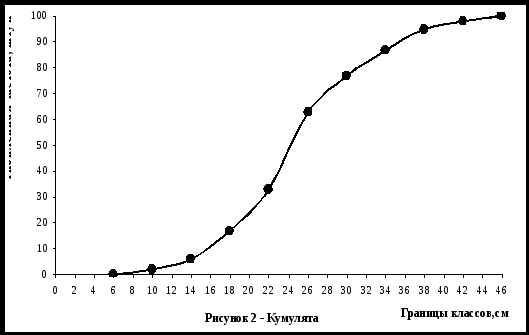   В курсовой работе произвести расчёт средней арифметической взвешенной, моду и медиану по представленным формулам. Медиану определить и графическим способом. Кумуляту построить на отдельном листе миллиметровой бумаги, формата А4.
Показателем, характеризующим меру скошенности ряда распределения является асимметрия. Она отражает меру отклонения распределения частот от симметричного их распределения относительно максимальной ординаты. Скошенность (асимметрия) ряда может быть левосторонней и правосторонней. Степень асимметрии можно определить несколькими способами:
Первый способ определения показателя асимметрии  где KАs – коэффициент асимметрии  - средняя величина выборочной совокупности (24,88 см) - мода (23,87 см)σ – средне квадратическое отклонение (стандартное отклонение) (7,45 см) Подставляя в приведённую формулу вычисленные параметры ряда распределения (данные по большой выборке) получаем: = 24,88 см = 23,87 смσ = 7,45 см  Иногда можно значение моды заменить медианой, что также характеризует асимметрию. Второй способ определения показателя асимметрии по формуле:  где  - отклонение средних классов (групповых вариант) от средней величины, смni – частоты классов, шт σ – стандартное отклонение N – объём совокупности, шт Для расчёта численного значения показателя асимметрии необходимо составить таблицу вспомогательных величин Например имеем следующие данные ряда распределения (большая выборка): Таблица 1.7 Расчёт вспомогательных величин для вычисления показателя асимметрии
= 24,88 смσ = 7,45 см σ 3= 413,4936 см 3 N = 100 шт Тогда подставляя полученные данные в приведённую формулу получаем численное значение показателя асимметрии:  Далее вычисляют ошибку и достоверность показателя асимметрии по следующим формулам. Ошибка показателя асимметрии:  Например:  Оценка достоверности по t – критерию Стьюдента:  Например: 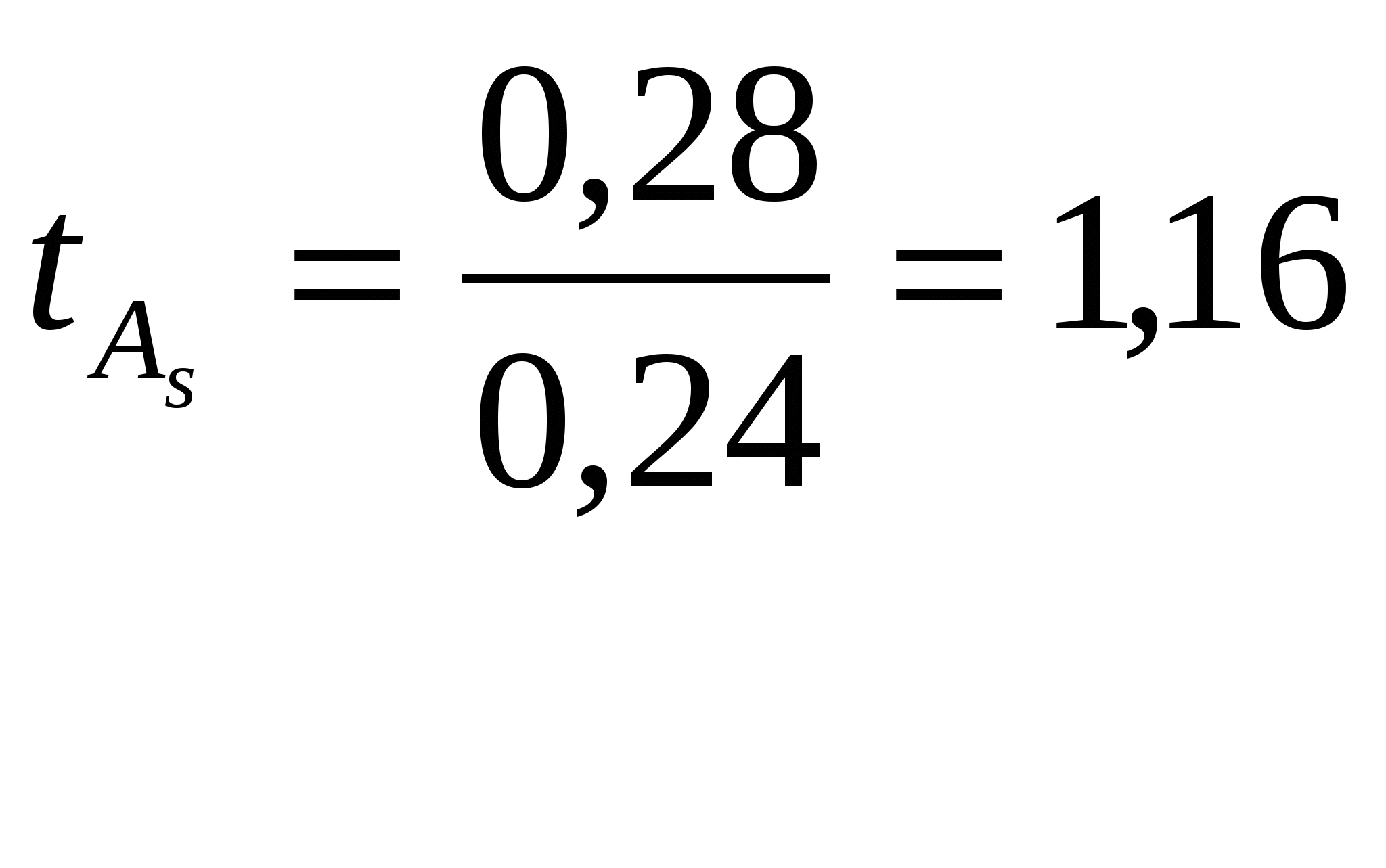 Для оценки достоверности фактическое значение t – критерия Стьюдента необходимо сравнить со стандартным на 5 % уровне значимости, при числе степеней свободы равным бесконечности k = ∞ (t 05 = 1,960). По приведённому примеру, сравнив фактическое значение критерия со стандартным, можно сделать вывод о том, что опытное распределение деревьев по ступеням толщины близко к симметричному, так как  .В таблице 1.8 представлены данные о силе смещения вершины кривой, по абсолютной величине показателя асимметрии. В курсовой работе сделать вывод о кривой ряда распределения. Таблица 1.8 Сила смещения вершины кривой
|
, см 3