Новая методичка статистика. 1 Расчёт основных статистических показателей для выборочных совокупностей

• Название: 1 Расчёт основных статистических показателей для выборочных совокупностей
• Дата: 16.02.2018
• Размер: 1.22 Mb.
• Имя файла: Новая методичка статистика.doc
• Тип: Документы; #36650
• страница: 5 из 11

Например: пользуясь вычисленными данными асимметрии можно сделать вывод, что смещение кривой малое, а саму кривую ряда распределения можно считать симметричной, так как

Если показатель асимметрии имеет знак «+», то вершина кривой скошена влево от центра распределении (асимметрия левосторонняя), а если знак «–», то вершина кривой скошена вправо (асимметрия правосторонняя).

Показателем, характеризующим меру крутости или вытянутости ряда распределения, является эксцесс. Он отражает степень отклонения эмпирической кривой распределения частот от симметричной куполообразной кривой на своей вершине.

Эксцесс можно определить несколькими способами:

1. 
   используя отношение отклонения вариант от средней величины в четвёртой степени и четвёртую степень среднеквадратического отклонения;
   
2. 
   используя моменты эмпирического распределения ряда.
   

Первый способ определения показателя эксцесса по формуле:



где - отклонение средних классов (групповых вариант) от средней величины, см

n_i – частоты классов, шт

σ – стандартное отклонение

N – объём совокупности, шт

Для расчёта численного значения показателя асимметрии необходимо составить таблицу вспомогательных величин

Например имеем следующие данные ряда распределения (большая выборка):
Таблица 1.9 Расчёт вспомогательных величин для вычисления показателя эксцесса

Групповая варианта (хi), см	Частота, (ni) шт	Четвёртая степень отклонения вариант от средней величины , см 4	ni×
1	2	3	4
8	2	81187,612	162375,225
12	4	27520,952	110083,808
16	11	6218,016	68398,180
20	16	567,126	9074,010
24	30	0,600	17,991
28	14	94,759	1326,620
32	10	2569,922	25699,222
36	8	15290,411	122323,285
40	3	52264,544	156793,632
44	2	133644,642	267289,284
Сумма	100	319358,583	923381,256

= 24,88 см

σ = 7,45 см σ ⁴= 3080,5275 см ⁴

N = 100 шт

Тогда подставляя полученные данные в приведённую формулу получаем численное значение показателя асимметрии:



Далее вычисляют ошибку и достоверность показателя эксцесса по следующим формулам.

Ошибка показателя эксцесса:



для сравнительно небольших по численности рядов распределения

Например:

Оценка достоверности по t – критерию Стьюдента:



Например: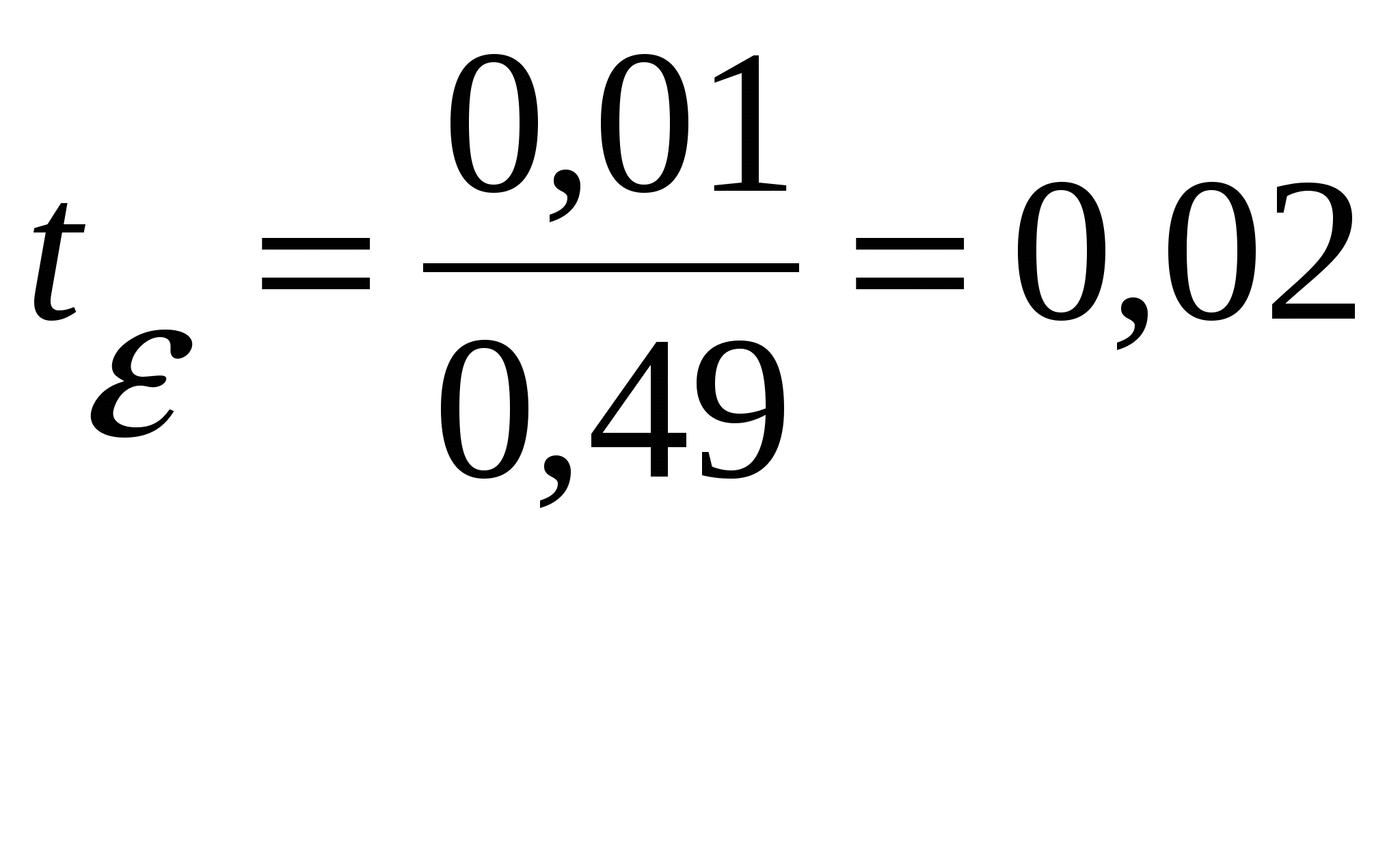

Для оценки достоверности фактическое значение t – критерия Стьюдента необходимо сравнить со стандартным на 5 % уровне значимости, при числе степеней свободы равным бесконечности k = ∞ (t ₀₅ = 1,960).

По приведённому примеру, сравнив фактическое значение критерия со стандартным, можно сделать вывод о том, что опытное распределение деревьев по ступеням толщины близко к симметричному, так как .

Отрицательное значение показателя эксцесса не может быть меньше, чем -2. Это указывает на то, что данная выборка состоит из вариант относящихся к разным независимым совокупностям. Положительного предела эксцесс не имеет. Чем меньше численное значение эксцесса, тем ближе распределение к симметричному. Если эксцесс меньше 0,4, то вытянутость ряда незначительная.

Если показатель эксцесса имеет знак «+», то вершина кривой приподнята относительно центра распределении (кривая островершинная), а если знак «–», то вершина кривой опущена (кривая плосковершинная или туповершинная).
Например:

Пользуясь вычисленными данными эксцесса можно сделать вывод, что вытянутость ряда незначительная, так как .
Третий способ определения показателей асимметрии и эксцесса с использованием моментов ряда распределения
Моменты распределения – это средние степени отклонений вариант от средней величины или от произвольного числа (условное начало) или от нуля. В связи с этим различают моменты: центральные, условные, начальные. В практике вычисляют ещё и основные моменты, используя численные значения центральных моментов и величины стандартного отклонения.

Степень, в которую возводятся отклонения – это порядок момента.

Моменты не имеют самостоятельного интереса, но с их помощью можно избежав громоздких вычислений, определить все основные статистические показатели ряда распределения.

Моменты распределения можно рассчитать либо способом сумм, либо способом произведений. Последний способ считается наиболее удобным.

Далее в таблице 1.10 приводится схема расчёта моментов.

Таблица 10. Расчёт моментов распределения способом сумм

Групповая варианта (хi), см	Частота, (ni) шт	Условные отклонения ai	Условные отклонения в различной степени
			ai × ni	ai2 × ni	ai3 × ni	ai4 × ni	ai + 1	(ai+1)×ni
1	2	3	4	5	6	7	8	9
8	2	- 4	- 8	32	- 128	512	- 3	162
12	4	- 3	- 12	36	- 108	324	- 2	64
16	11	- 2	- 22	44	- 88	176	- 1	11
20	16	- 1	- 16	16	- 16	16	0	0
24	30	0	0	0	0	0	1	30
28	14	1	14	14	14	14	2	224
32	10	2	20	40	80	160	3	810
36	8	3	24	72	216	648	4	2048
40	3	4	12	48	192	768	5	1875
44	2	5	10	50	250	1250	6	2592
Сумма	100		22	352	412	3868		7816

- в первый столбец вписаны классовые варианты – x_i,см;

- во втором столбце – эмпирическая частота n_i,шт.;

- в третьем столбце производим (кодировку данных) расчёт , где

А – групповая варианта, которой соответствует наибольшее значение частоты (это условное начало) .По выше приведённой таблице А = 24 см, т.к. частота данного класса будет максимальной.

С – величина классового интервала, равна 4 см

Расчёт в данном столбце аналогичен расчёту в пункте 1.2.3 таблица 1.6.

В столбцах: 2, 4, 5, 6, 7, 9 находят сумму.

Прежде, чем приступить к вычислению моментов, необходимо произвести проверку вычислений. Сумма чисел 9 столбца должна быть равна выражению:


Например:

7816 = 3868 + (4 × 412) + (6 × 352) + (4 × 22) + 100;

7816 = 3868 +1648 +2112 + 88 + 100;

7816 = 7816; следовательно, суммы вычислены верно.
Далее приступаем к расчёту моментов распределения и основных статистических показателей ряда распределения. Моменты вычисляются с точностью до 0,0001.

1. Находим условные моменты ряда распределения по формулам:

Условный момент первого порядка:

Например:

Условный момент второго порядка:

Например:

Условный момент третьего порядка:

Например:

Условный момент четвёртого порядка:

Например:

2. Находим центральные моменты ряда распределения по формулам:
Центральный момент второго порядка:
Например:
Центральный момент третьего порядка:
Например:
Центральный момент четвёртого порядка:
Например:
3. Производим проверку найденных моментов распределения по

формулам:
Центральный момент третьего порядка:
Например:
Центральный момент четвёртого порядка:
Например:
4. Вычисляем статистические показатели ряда распределения:
- среднюю арифметическую взвешенную величину по формуле:



где А – групповая варианта, которой соответствует наибольшее значение частоты (это условное начало) .По выше приведённой таблице А = 24 см..

С – величина классового интервала, равна 4 см
Например: см.

- среднеквадратическое (стандартное) отклонение в единицах классового интервала по формуле :



Например: см

Аналогичные данные были получены в пункте 1.2.3, что ещё раз подтверждает правильность расчётов моментов ряда распределения.

- среднеквадратическое (стандартное) отклонение по формуле:



Например:
5. Определяем численное значение показателя асимметрии по формуле: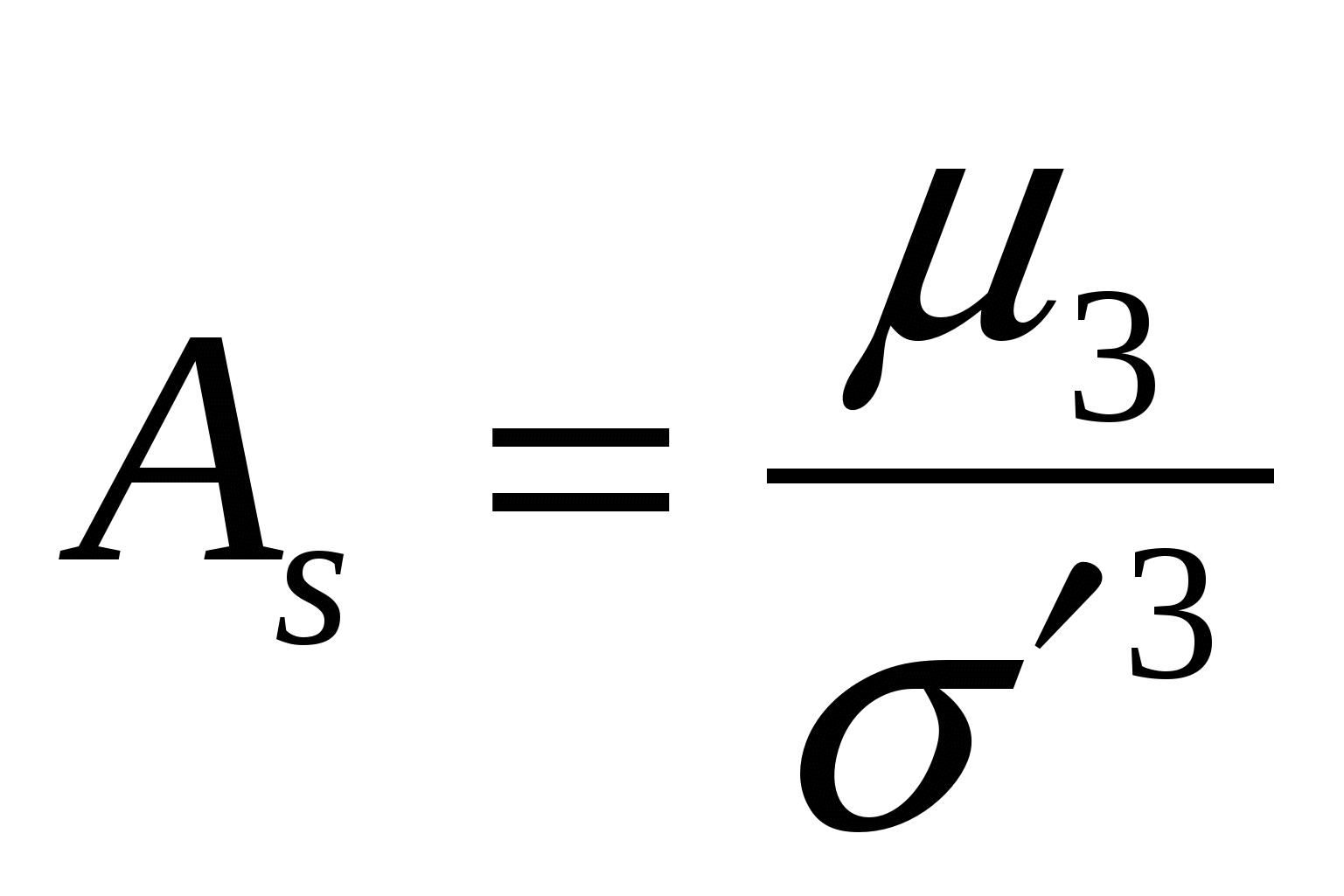



Например:
6. Определяем численное значение показателя эксцесса по формуле: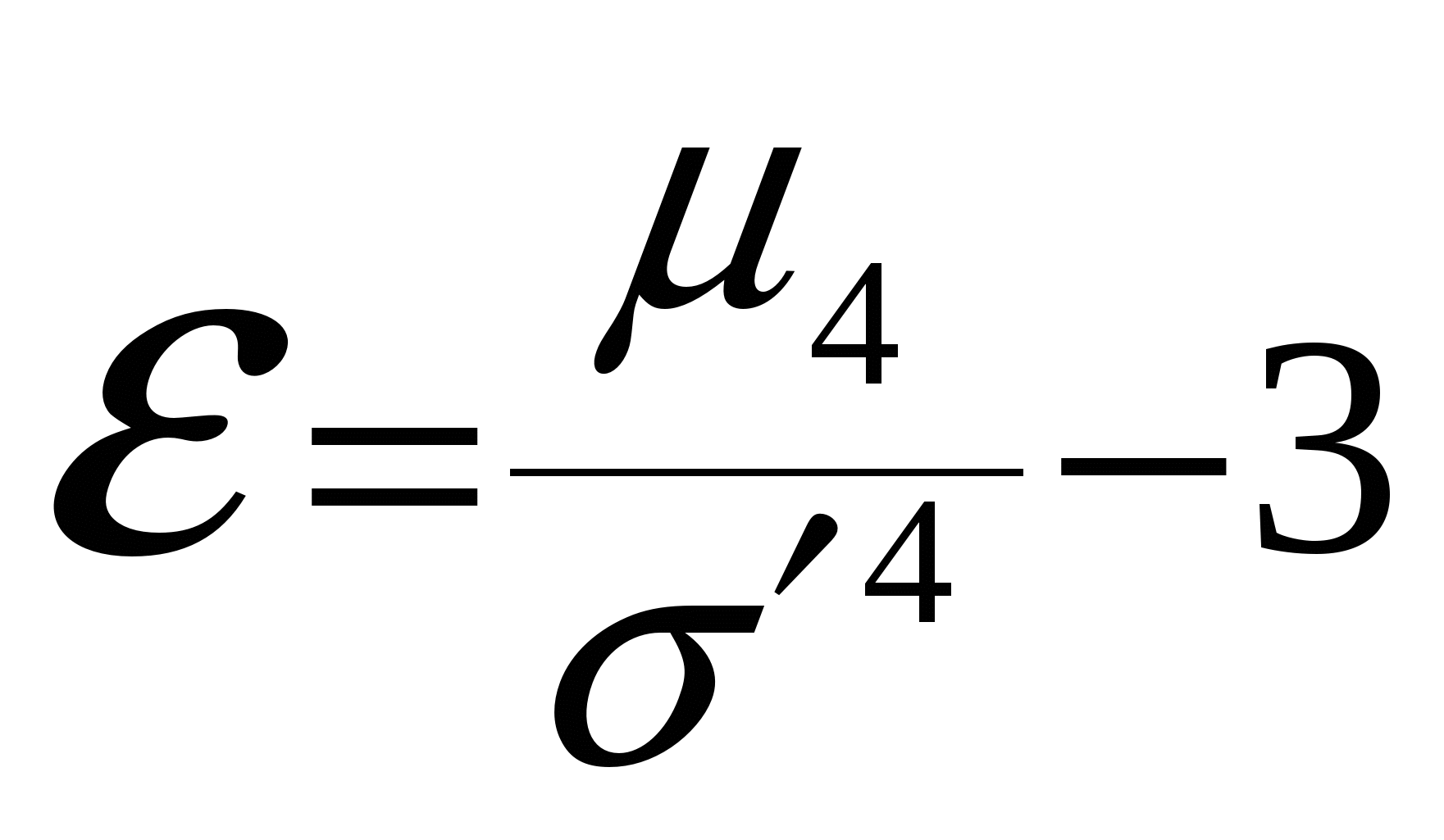



Например:
7. Далее вычисляют ошибку и достоверность показателя асимметрии и эксцесса по следующим формулам.

Ошибка показателя асимметрии:

Например:

Оценка достоверности по t – критерию Стьюдента:

Например: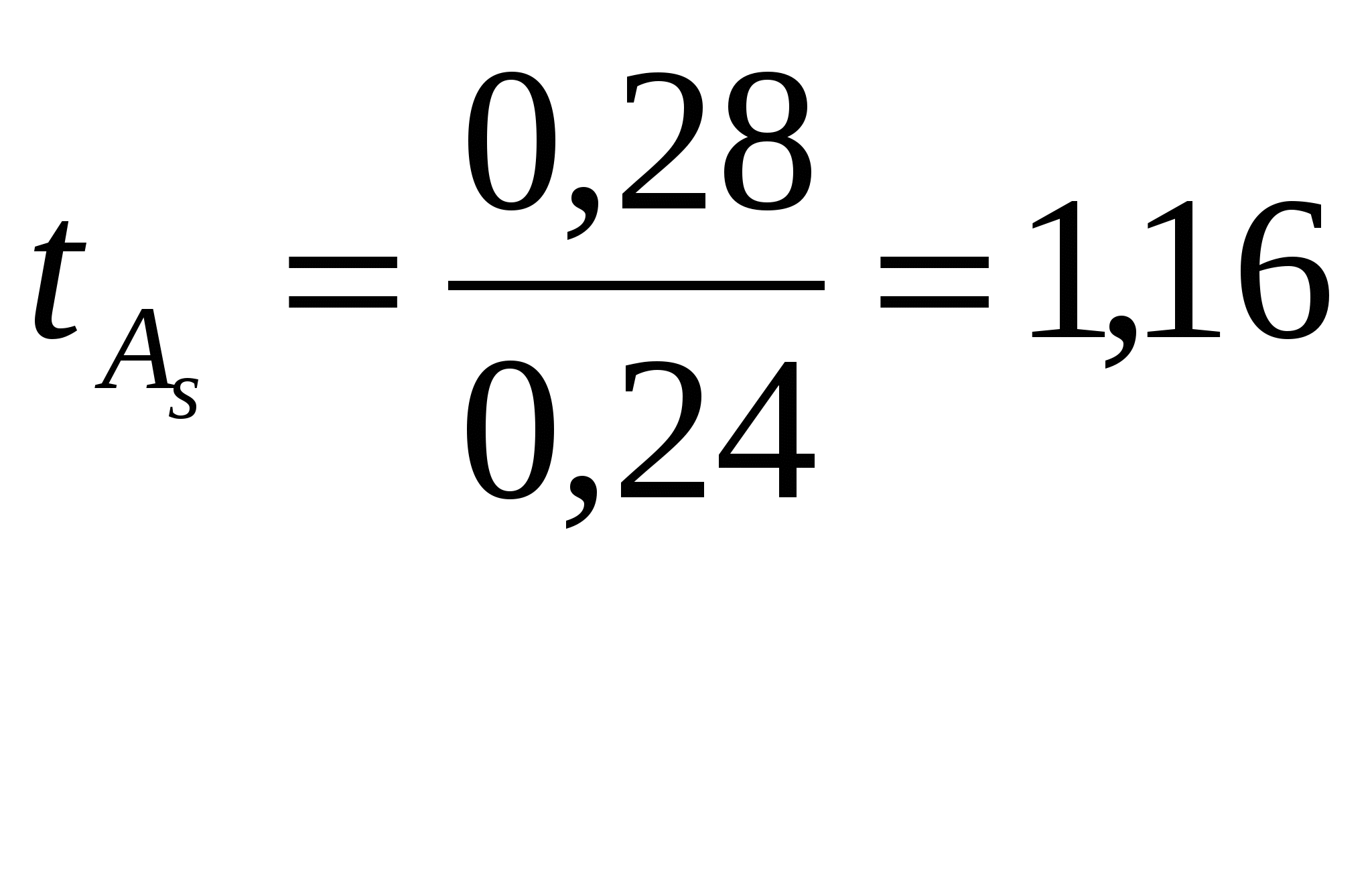

Для оценки достоверности фактическое значение t – критерия Стьюдента необходимо сравнить со стандартным на 5 % уровне значимости, при числе степеней свободы равным бесконечности k = ∞ (t ₀₅ = 1,960).

По приведённому примеру, сравнив фактическое значение критерия со стандартным, можно сделать вывод о том, что опытное распределение деревьев по ступеням толщины близко к симметричному, так как .

Ошибка показателя эксцесса:

Например:

Оценка достоверности по t – критерию Стьюдента:

Например: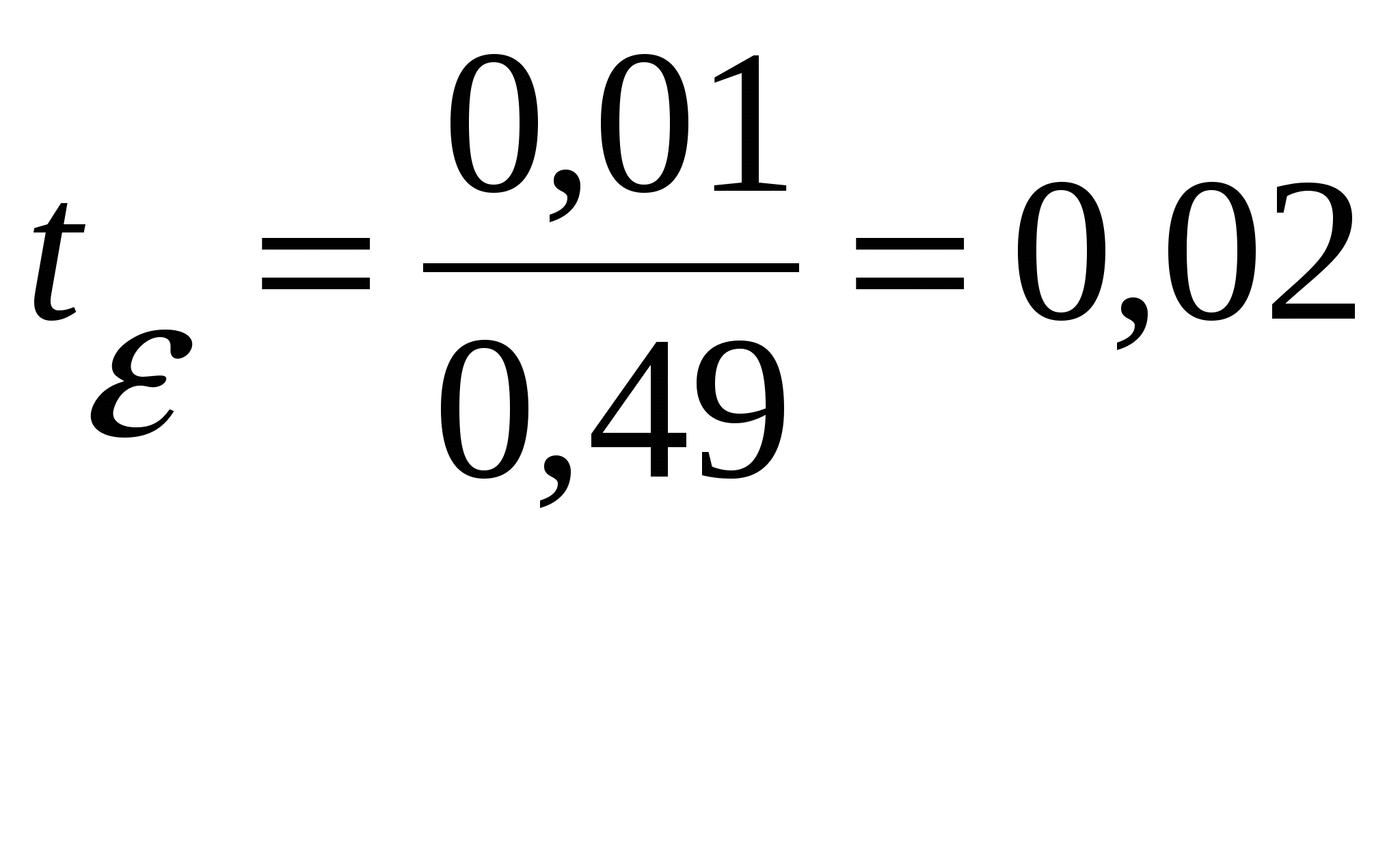

Для оценки достоверности фактическое значение t – критерия Стьюдента необходимо сравнить со стандартным на 5 % уровне значимости, при числе степеней свободы равным бесконечности k = ∞ (t ₀₅ = 1,960).

По приведённому примеру, сравнив фактическое значение критерия со стандартным, можно сделать вывод о том, что опытное распределение деревьев по ступеням толщины близко к симметричному, так как .