Новая методичка статистика. 1 Расчёт основных статистических показателей для выборочных совокупностей
 Скачать 1.22 Mb. Скачать 1.22 Mb.
|
|
2.0 Теоретические законы распределения случайных величин
Этот тип непрерывного распределения, открытого в 1733 г. Муавром, имеет плотность распределения: 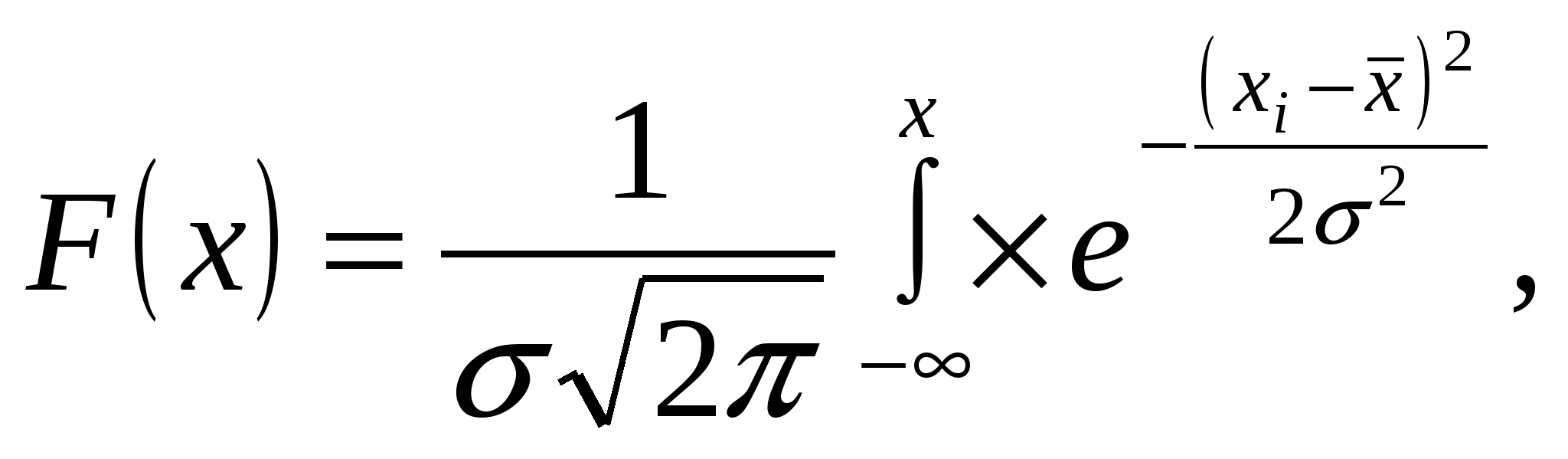 где x - среднее значение; σ - стандартное отклонение. Графически плотность распределения F(x) представляет собой симметричную относительно точки х = x колоколообразную кривую, форма которой зависит от величины среднеквадратического отклонения, которое является параметром масштаба, а положение определяется значением средней. Для расчета теоретических частот эмпирического ряда используют таблицы значений F(t), составленные для нормированного отклонения, которое рассчитывается по формуле: Расчет теоретических частот эмпирического ряда производят следующим образом:
где n – объем выборки; С – классовый интервал; σ – стандартное отклонение; f (t) – плотность вероятности нормального распределения (ордината кривой нормального распределения). Пример расчета теоретических частот для кривой нормального распределения приведен в таблице. Таблица 2.1 Вычисление выравнивающих частот по уравнению Лапласа – Гаусса
- в первый столбец вписаны классовые варианты – xi,см; - во втором столбце – эмпирическая частота ni,шт.; - в третьем столбце центральное отклонение - в четвертом столбце – нормированное отклонение, показывающее, насколько «σ» отдельные члены данной совокупности отклоняются от среднего уровня учитываемого признака. Нормированное отклонение рассчитывается по формуле: где xi – групповая варианта; - в пятом столбце – значение функции для нормированного отклонения – f(t); - в шестом столбце – теоретически рассчитанная частота – n,, штук. Например: Далее графически изображается распределение эмпирических и теоретических частот по классам. Для этого по оси абсцисс откладываются классы или групповые варианты, а по оси ординат частоты классов. 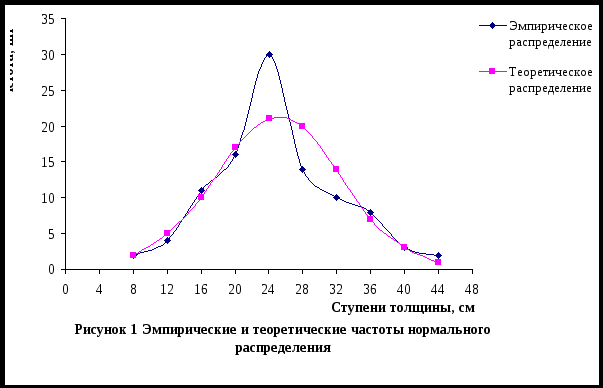 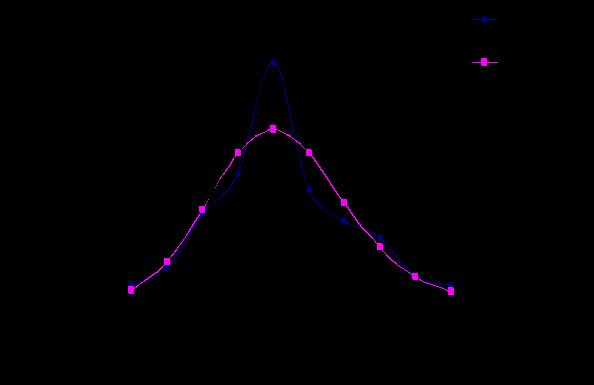  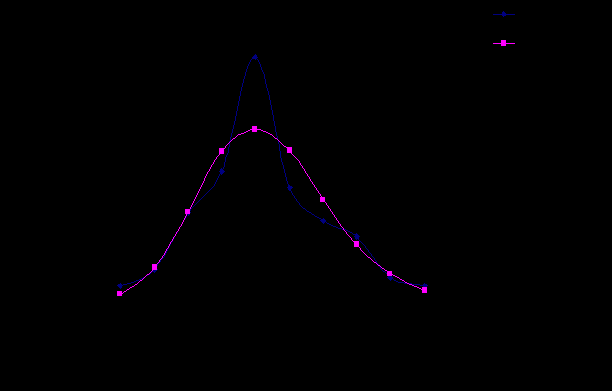 3. Критерии оценки статистических гипотез Понятие статистической гипотезы предполагает проведение статистической оценки в подтверждение или отклонение рассматриваемого предположения. Статистические гипотезы подразделяют на виды: - параметрические (требуется вычисление параметров распределения); - непараметрические (не требуется вычисления параметров распределения). На основании статистической оценки решается вопрос: принять или отвергнуть гипотезу. Для решения этого вопроса требуется выполнить следующее: - рассмотреть не только проверяемую гипотезу, но и исключающую ее альтернативную гипотезу; - выбрать статистический критерий, по которому дается заключение о наличии или отсутствии проверяемой или альтернативной гипотезы. Чаще всего используют так называемую нулевую гипотезу (Н0), т.е. предположение о том, что между генеральными параметрами сравниваемых групп разница равна нулю и различия, наблюдаемые между выборочными показателями, носят случайный характер (т. е. обусловлены случайным характером формирования совокупности). Критерии проверки статистических гипотез Истинность принятой гипотезы проверяют с помощью критериев значимости, т.е. специально выработанных случайных величин, функции, распределения которых известны. Для каждого критерия составлена таблица, в которой содержатся критические точки, отвечающие определенным числам (k,ν) и принятым уровням значимости. Уровень значимости - значение вероятности, при котором различия, наблюдаемые между выборочными показателями можно считать не существенными. В исследовательских работах обычно пользуются 5%-ным уровнем значимости, которому отвечает вероятность P=0,05. Схема использования статистических критериев (К) в области лесного дела при строгом доказательстве нулевой гипотезы К05 > Кф > К01   Не отвергается Отвергается ,   Нулевая гипотеза где Кф- значение фактически полученного критерия; К05, К01 - значения критериев на 5% - ном и 1% - ном уровнях значимости. 3.1. Статистическое сравнение эмпирического распределения с теоретическим по критерию χ- квадрат Пирсона Критерий χ- квадрат (χ 2) впервые был предложен К. Пирсоном в 1901 году. Пользуясь этим критерием можно произвести оценку различий между эмпирическим и теоретическим распределением частот. Он рассчитывается по формуле: 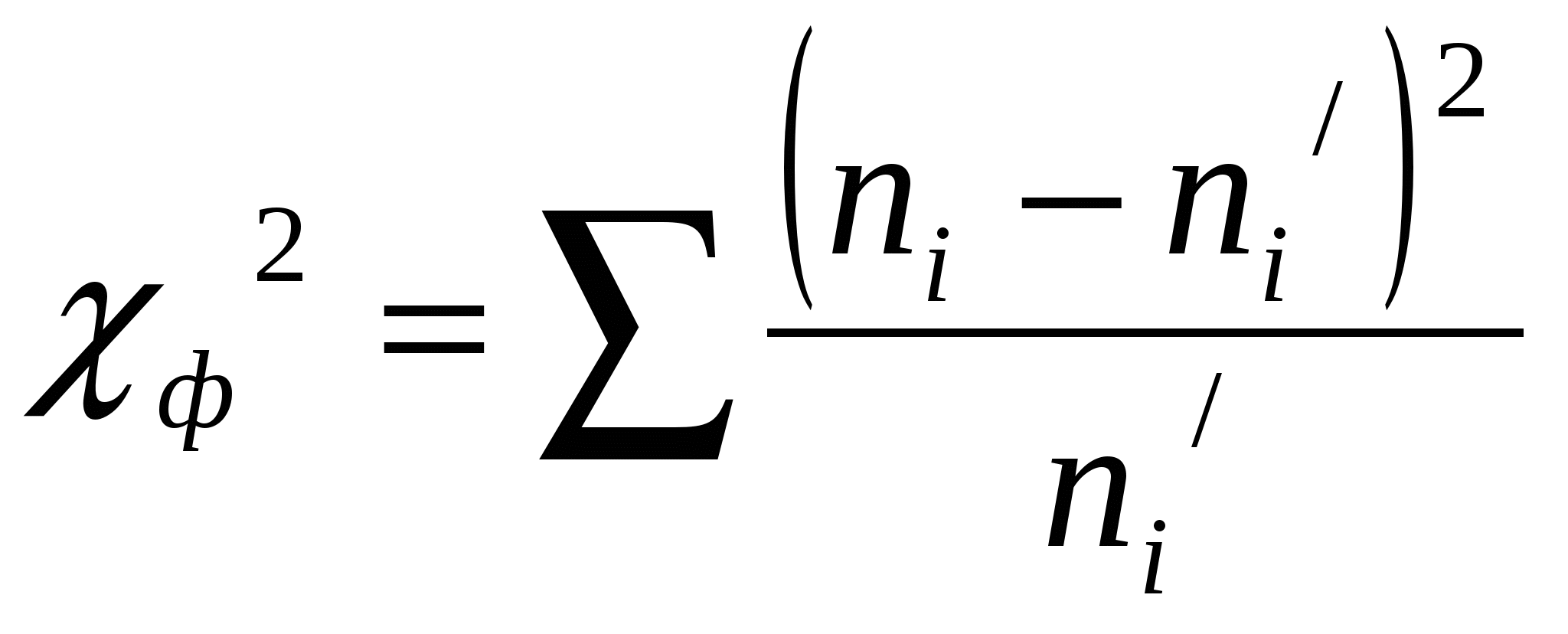 , ,где ni – эмпирическая частота; ni'- теоретическая частота. Оценка значимости критерия χ 2 производится по специальной таблице (приложение 3 учебника Герасимов, Хлюстов), в которой приведены стандартные значения этого критерия (χ 2st) для трех пороговых уровней доверительной вероятности и для разных чисел степеней свободы. Число степеней свободы равно числу классов без трех k=n-3. Если χ 2ф< χ 2st , то расхождение между эмпирическим и теоретическим распределением подчиняется тому закону, по которому рассчитаны теоретические частоты. В таблице 3.1 приводится порядок расчета критерия согласия χ 2 - Пирсона. Таблица 3.1 Оценка различий между эмпирическим и теоретическим распределением деревьев сосны по диаметру на высоте груди
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
