Новая методичка статистика. 1 Расчёт основных статистических показателей для выборочных совокупностей

• Название: 1 Расчёт основных статистических показателей для выборочных совокупностей
• Дата: 16.02.2018
• Размер: 1.22 Mb.
• Имя файла: Новая методичка статистика.doc
• Тип: Документы; #36650
• страница: 10 из 11

Вычисление вспомогательных величин:

см

м

где n – это объём выборочной совокупности (по примеру n = 29)

;

;

,
Формула расчета коэффициента корреляции: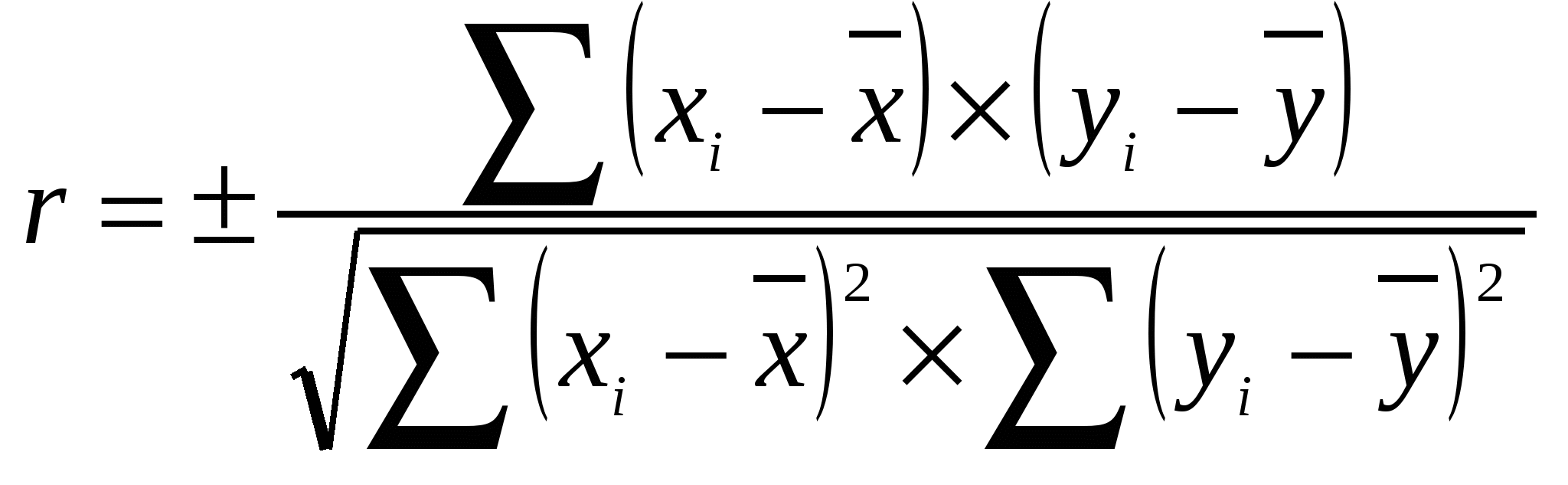

.

Например:.

Ошибка коэффициента корреляции:

.

Например: .

Значимость корреляции: .

Например:.

Число степеней свободы: .

Например:.

Для определения значимости коэффициента корреляции устанавливается стандартное значение t – критерий Стьюдента на 5 % уровне значимости.

t – критерий Стьюдента на 5 % уровне значимости (определяется по таблице учебника) исходя из числа степеней свободы

t₀₅ = 2,045

t _r= 7,36 > t₀₅, значит корреляция значима.

Расчет вспомогательных величин для вычисления корреляционного отношения приведен в таблице 5.2.

Для расчёта вспомогательных величин необходимо произвести группировку данных по независимой переменной или разбить все данные на классы с равной величиной классового интервала.

В курсовой работе данные группируются в ступени толщины с величиной классового интервала 4 см. ступени толщины не пропускаются, при этом число деревьев в ступени должно быть не менее двух.


Таблица 5.2 Расчет вспомогательных величин для вычисления корреляционного отношения

Ступени толщины (ч/з 4 см)	Диаметр, xi, см	Высота yi, м	yусл.	Отклонения
				α =yi - y	α2	Δy = =yi-yусл.	Δy2
1	2	3	4	5	6	7	8
12	11,3 12,0 13,8	13,6 15,3 15,8	14,9	-6,53 -4,83 -4,33	42,64 23,32 18,75	-1,3 0,4 0,9	1,69 0,16 0,81
16	14,9 14,7 14,7 15,7 14,8 16,2 17,3 16,5	18,1 19,5 15,3 18,1 17,6 17,5 18,6 19,5	18,03	-2,03 -0,63 -4,83 -2,03 -2,53 -2,63 -1,53 -0,63	4,12 0,40 23,33 4,12 6,4 6,92 2,34 0,40	0,07 1,47 -2,73 0,07 -0,43 -0,53 0,57 1,47	0,05 2,16 7,45 0,0003 0,18 0,28 0,32 2,16
и т.д	…	…	…	…	…	…	…
					∑ α2 251,46		∑ Δ y2 73,15

y_{условное}- средняя высота ступени толщины.
Например:.

Формула расчета корреляционного отношения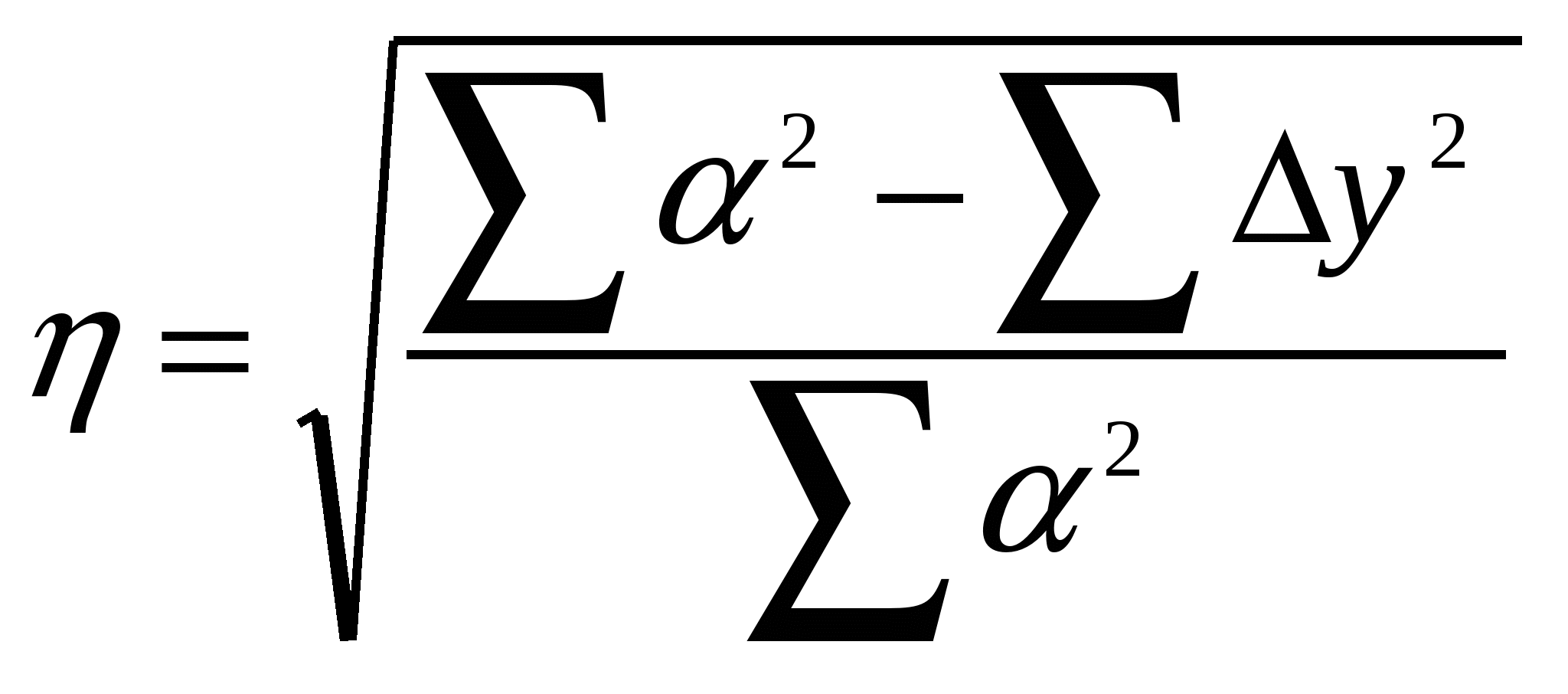

.

Например:.

Ошибка корреляционного отношения

.

Например:.
Значимость корреляционного отношения

.

Например:.

Число степеней свободы:

.

Например:.

t – критерий Стьюдента на 5 % уровне значимости (определяется по таблице учебника) исходя из числа степеней свободы

t₀₅ = 2,045 (определяется по таблице учебника),

t _r= 7,36 > t₀₅, значит корреляция значима.
Мера линейности корреляции

.

Например:.

Основная ошибка

.

Например:.

По отношению меры линейности к основной ошибке судим о линейности связи.

Например:, связь приблизительно можно считать линейной.

Степень тесноты связи между изучаемыми признаками производится по величине корреляционного отношения с помощью таблицы 5.3.
Таблица 5.3 Таблица для определения тесноты связи

Степень тесноты связей	Величина корреляционного отношения
слабая	0-0,3
умеренная	0,31-0,5
значительная	0,51-0,7
высокая	0,71-0,9
очень высокая	0,91 и выше

Статистическое заключение

По результатам корреляционного анализа можно сделать вывод, что взаимосвязь между диаметром и высотой ствола по направлению – прямая, по тесноте – высокая, по форме – близка к линейной.
6.0 Расчет среднеквадратических ошибок
При проведении полевого и других опытов проявляются три вида ошибок. Ошибка – это расхождение между различными значениями выборочной совокупности или отдельных наблюдений от истинных значений измеряемых величин.

Основные свойства ошибок и причины их возникновения

Случайные ошибки – это ошибки, возникающие под воздействием факторов, действие которых не значительно и их нельзя выделить и учесть отдельно. Случайные ошибки в полевом опыте неизбежны. Математическая статистика дает методы их определения. Случайные ошибки имеют знак «±». Они взаимопогашаются.

Систематические ошибки – искажают измеряемую величину в сторону преувеличения или преуменьшения в результате действия вполне определенной постоянной причины. Исключить действие этой причины можно путем применения правильной методики. Систематические ошибки имеют конкретный знак или «+» или «–». Они не взаимопогашаются.

Грубые ошибки (промахи) – возникают в результате нарушения основных требований полевого опыта. Грубые ошибки не погашаются, а результат бракуется.

Для математической обработки подходят лишь результаты наблюдений без систематических и грубых ошибок.

Пример расчета среднеквадратических ошибок при определении запаса древесины глазомерным способом приведен в таблице.
Таблица 6.1 Расчет среднеквадратических ошибок.

Определение запаса глазомерным способом первым таксатором

Запас, м3 / га		Откло-нение, %	Откло-нение с поправ-кой, %	Квадрат отклонений с поправкой, %	Расчет ошибок
Факти-ческий	Глазо-мерный
200	170	- 15,00	- 15,09	227,71	Систематическая ошибка: Δ = ± Σ откл / n Δ = ± 12,53/ 12 = 1,04% Поправка: Δ/ = ± ∆ / n = Δ/ = ± 1,04/ 12 = 0,09% Случайная ошибка: σ = ± 1913,18 / 11= ± 13,18% Ошибка для всех случаев: m σ = ± 13,18/ = = ± 3,46%
210	240	14,29	14,20	201,64
220	200	- 9,09	- 9,18	84,27
240	270	12,5	12,41	154,01
260	220	- 15,38	- 15,41	239,32
280	340	21,43	21,34	455,40
300	270	- 10,00	- 10,09	101,81
320	350	9,38	9,29	86,30
340	310	- 8,82	-8,91	79,39
360	400	11,11	11,02	121,44
380	350	- 7,89	-7,98	63,68
400	440	10,00	9,91	98,21
n = 12, n – количество площадок		∑ откл 12,53		СКО 1913,18

Для расчёта отклонения с поправкой поправку взять с противоположным знаком, не зависимо от знака отклонения.

Аналогичный расчет ошибок производится по результатам определения запаса глазомерным способом для второго таксатора. На основе сравнения среднеквадратических ошибок (случайных и ошибок для всех случаев) делаем вывод о работе двух таксаторов. Сравнительную оценку по случайной ошибке можно произвести в том случае, если её численное значение не превышает 10 %. В противном случае сравнение лучше сделать по ошибке для всех случаев.
Статистическое заключение

Работа по определению запаса глазомерным способом на пробных площадях, вторым таксатором выполнена более точно, так как его ошибка для всех случаев меньше, по сравнению с первым таксатором.

7.0 Регрессионный анализ
Постановка задачи

Математические выражения, отражающие причинно-следственные взаимосвязи и взаимодействия в системах (или модели связи) являются основными типами моделей, применяемых в области лесного дела. В качестве математической формы эмпирических моделей связи, в основном, используют регрессионные уравнения и реже – интерполяционные многочлены. В первом случае применяют различные модификации метода наименьших квадратов, позволяющие просто и достаточно надежно оценить статистическим путем разрабатываемую модель. Второй метод сводится к механической процедуре аналитического выражения числовых массивов.

Для вычисления коэффициентов регрессионных уравнений основным методом является метод наименьших квадратов, предложенный в начале XIX в. Лежандром и Гауссом. Требование метода наименьших квадратов заключается в том, что теоретические точки линии регрессии y должны быть получены таким образом, чтобы сумма квадратов отклонений от этих точек эмпирических значений была минимальной, то есть


7.1. Линейное уравнение с логарифмированием факторного признака
Для вычисления коэффициентов a и b для уравнения прямой с логарифмированием факторного признака



необходимо решить следующую систему уравнений: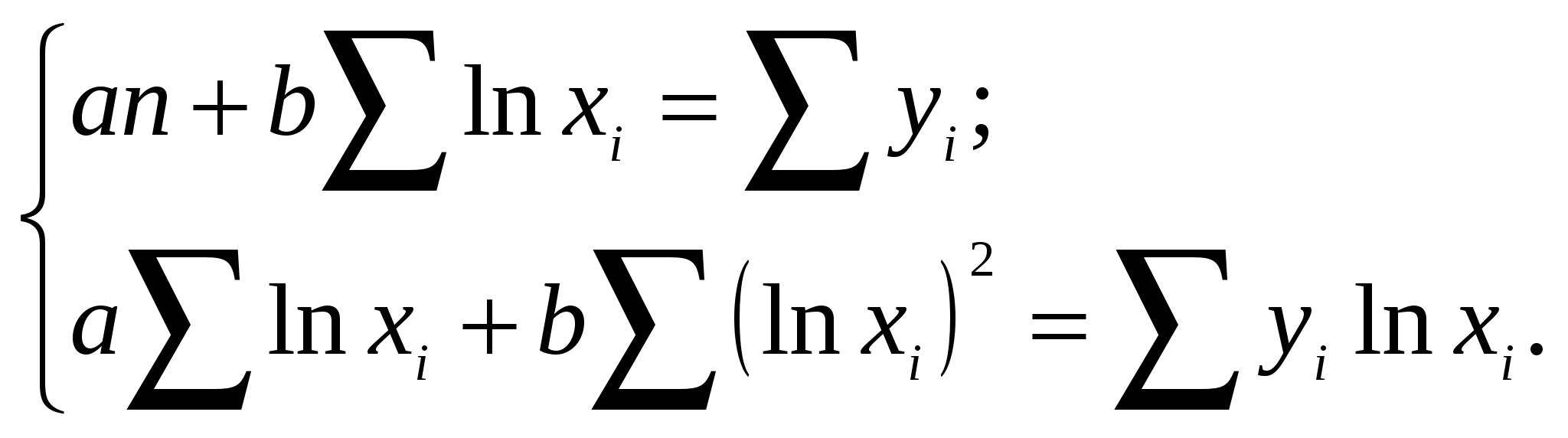



Решение системы относительно неизвестных a и b дает численные значения искомых коэффициентов: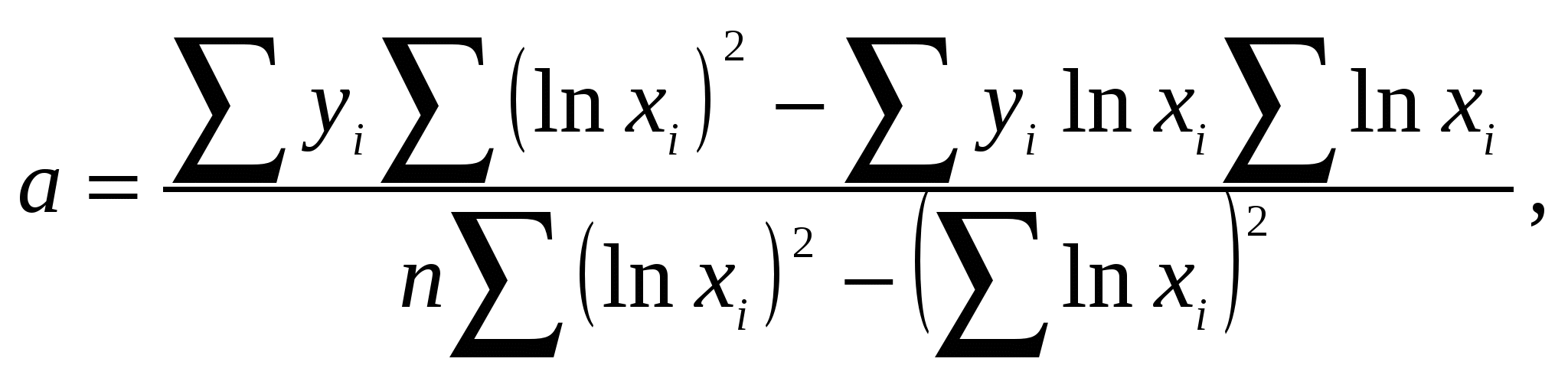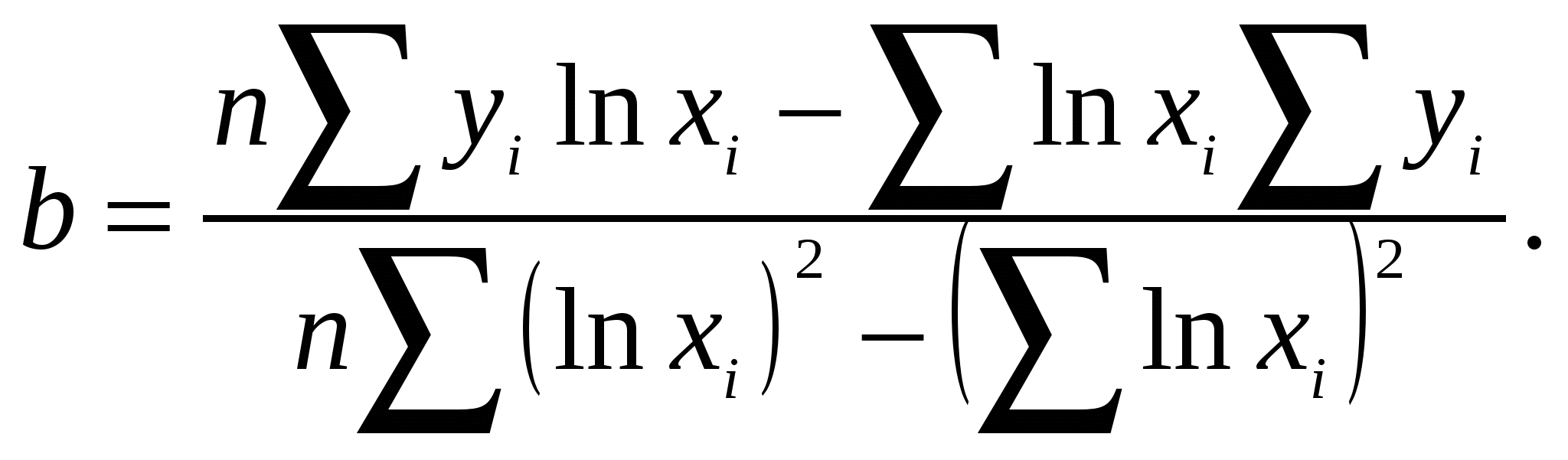





Пример: Найти уравнение регрессии, описывающее фактические значения высот по диаметрам в сосновом древостое, используя линейную модель с логарифмированием факторного признака.

Расчет вспомогательных величин для нахождения коэффициентов уравнения приведен в таблице 7.1.
Таблица 7.1 Расчет вспомогательных величин для нахождения коэффициентов a и b

Диаметр, xi , см	Высота, yi ,м	yi2	ln xi	(ln xi )2	yi×lnxi	yx = –14,69 + 11,42×ln xi	yi – yx	(yi –yx)2
1	2	3	4	5	6	7	8	9
8	9,5	90,25	2,08	4,32	19,75	9,04	0,46	0,21
12	13,4	179,56	2,48	6,17	33,3	13,66	- 0,26	0,07
16	16,3	265,69	2,77	7,69	45,19	16,95	- 0,65	0,42
и т.д.
360,0	264,2	6293,90	39,19	131,74	905,02	сумма	-6,65	7,81

Найдя вспомогательные величины по таблице 7.1 подставляем их в исходные выражения или в формулы определения коэффициентов а и в.

По приведённому примеру коэффициенты а и в соответственно равны:




Полученное уравнение регрессии имеет вид y_х = -14,69 + 11,42×ln x_i.

Далее в 7 колонке таблицы 7.1 вычисляются высоты деревьев по полученному уравнению: например y_x = –14,69 + 11,42×2,08 = 9,04 и так далее.

В 8 и 9 колонках находят расхождение между высотой опытной (колонка 2) и высотой полученной по уравнению (колонка 7) и квадрат этого отклонения.

Проверка значимости уравнения регрессии производим по F – критерию Фишера, который равен отношению общеё дисперсии к дисперсии остаточной.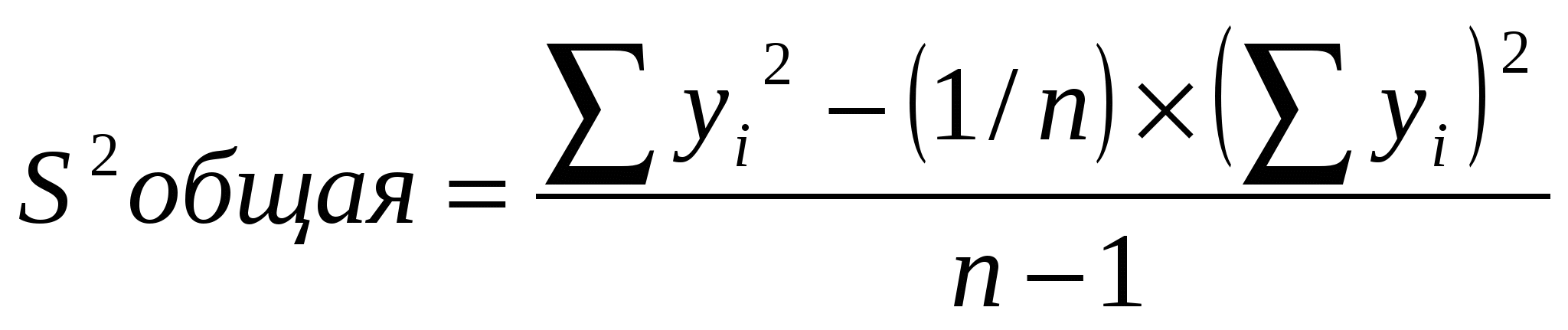







Например:





При сравнении фактического значения F – критерия с F – критерием стандартным на 5 или 1 % уровне значимости делаем заключение об адекватности модели. Если F_ф > F_st, то предложенная модель (уравнение) адекватно предсказывает изменение высот по диаметрам.

F_st берётся из приложения учебника, в зависимости от числа степеней свободы общей дисперсии (большая), и числа степеней свободы остаточной дисперсии (меньшая).

Число степеней свободы для общей дисперсии k₁=n-2

Число степеней свободы для остаточной дисперсии k₂=n-1

Для приведённого примера: k₁=n-2=12-2=10 k₂=n-1=12-1=11

F_st для 5 % уровня значимости равно 2,86.

Так как F_ф > F_st, то предложенная модель (уравнение) адекватно предсказывает изменение высот по диаметрам.
Представить графически изменение высот от диаметров для оценки адекватности модели по полученному уравнению. Построение графиков по исходным данным пунктирной линией (x_i ,y_i), по расчетным данным сплошной линией (x_i , y_x).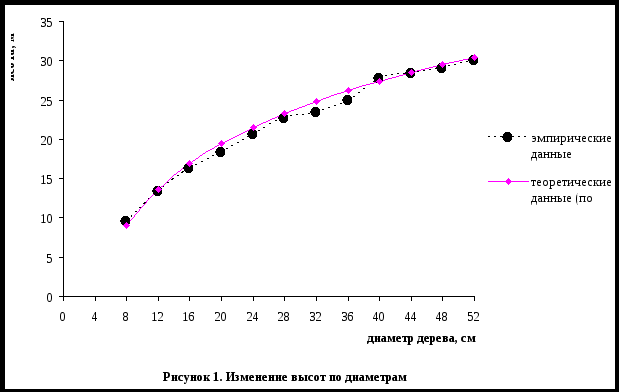


Статистическое заключение
По результатам регрессионного анализа можно сделать заключение, что линейное уравнение с логарифмированием факторного признака, представленное результатами опыта у = -14,69 + 11,42×ln x_i в 55,53 раза лучше описывает изменение зависимой переменной чем среднее значение аргумента.

7.2. Уравнение гиперболы
Для вычисления коэффициентов a и b гиперболической зависимости:



необходимо решить следующую систему уравнений: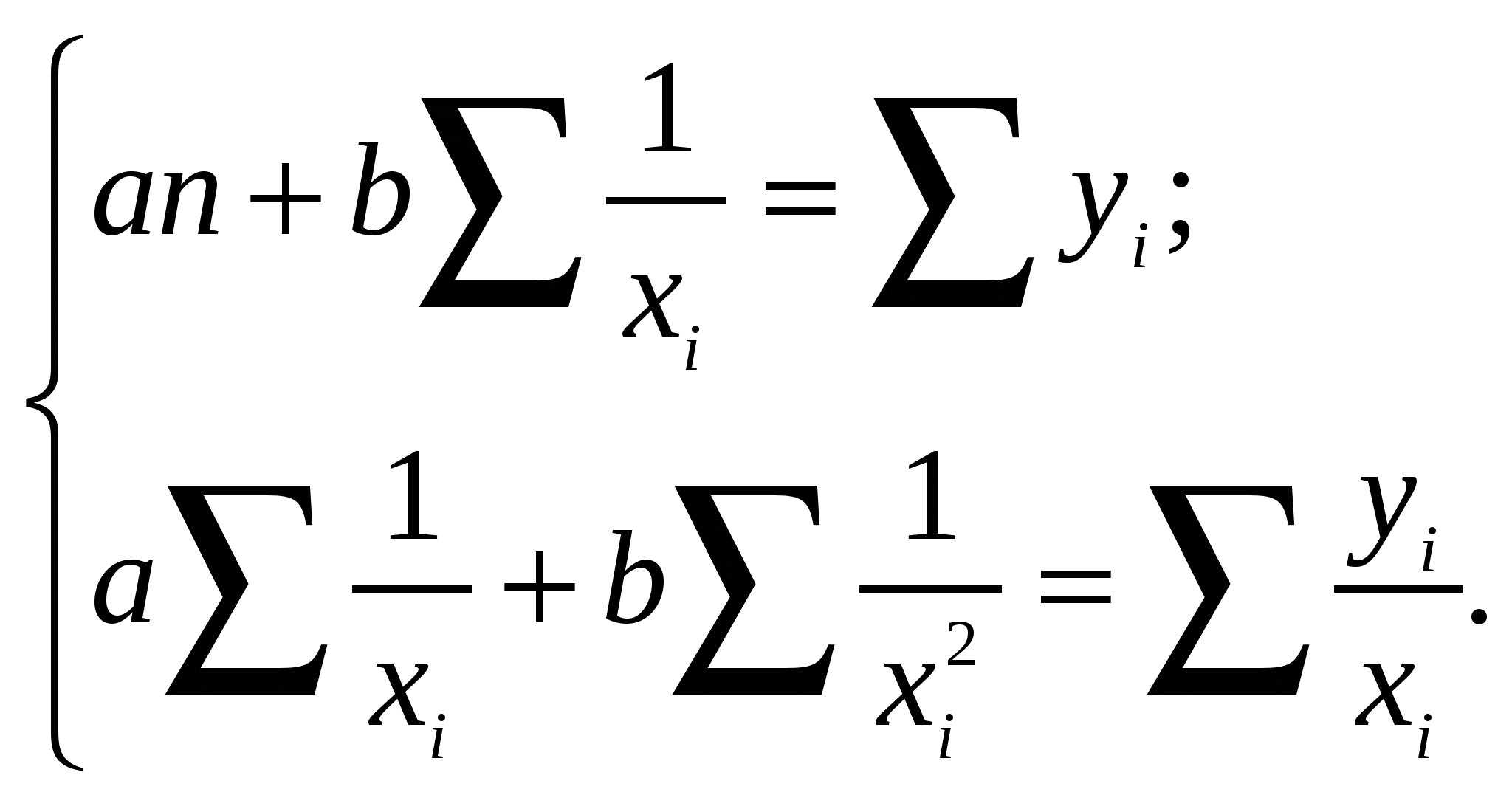



Результатом решения системы нормальных уравнений являются следующие выражения: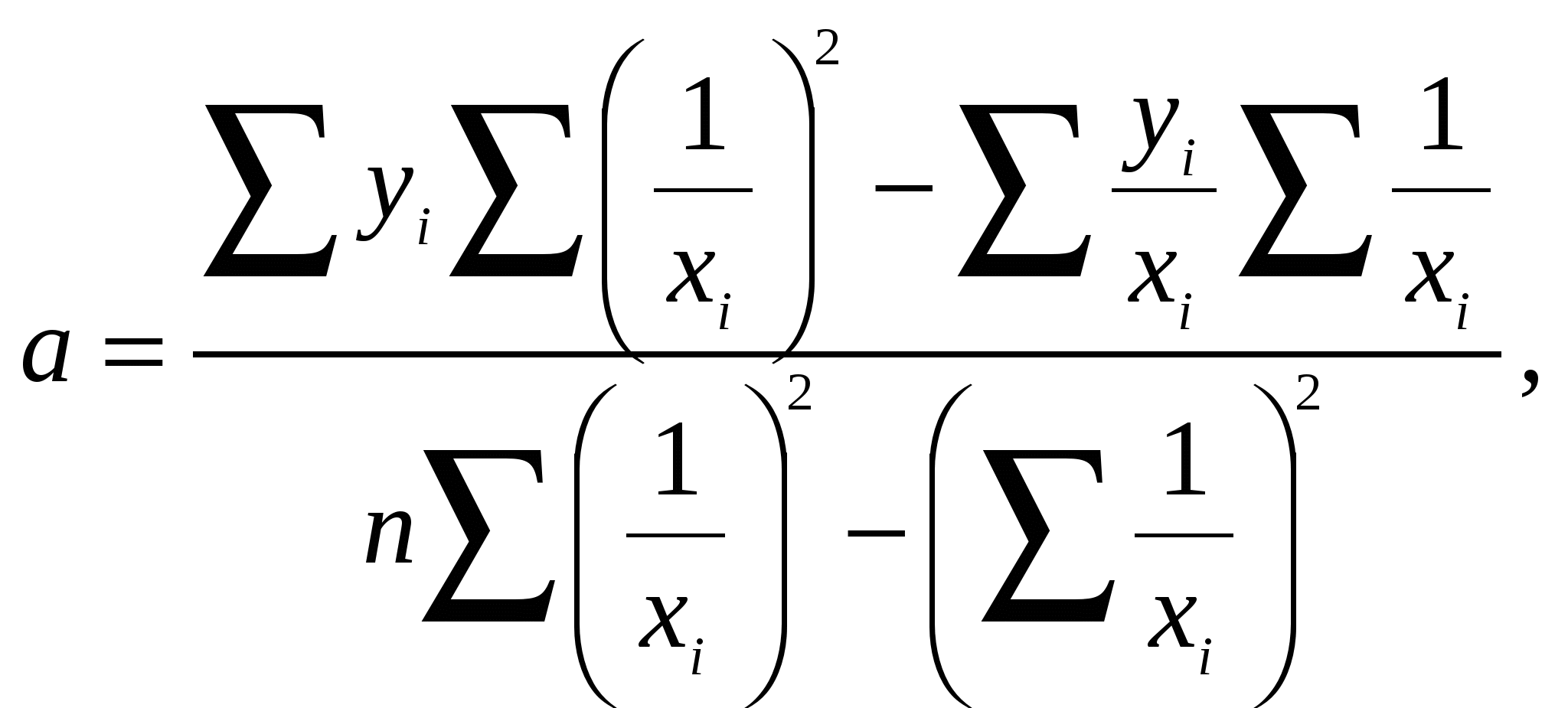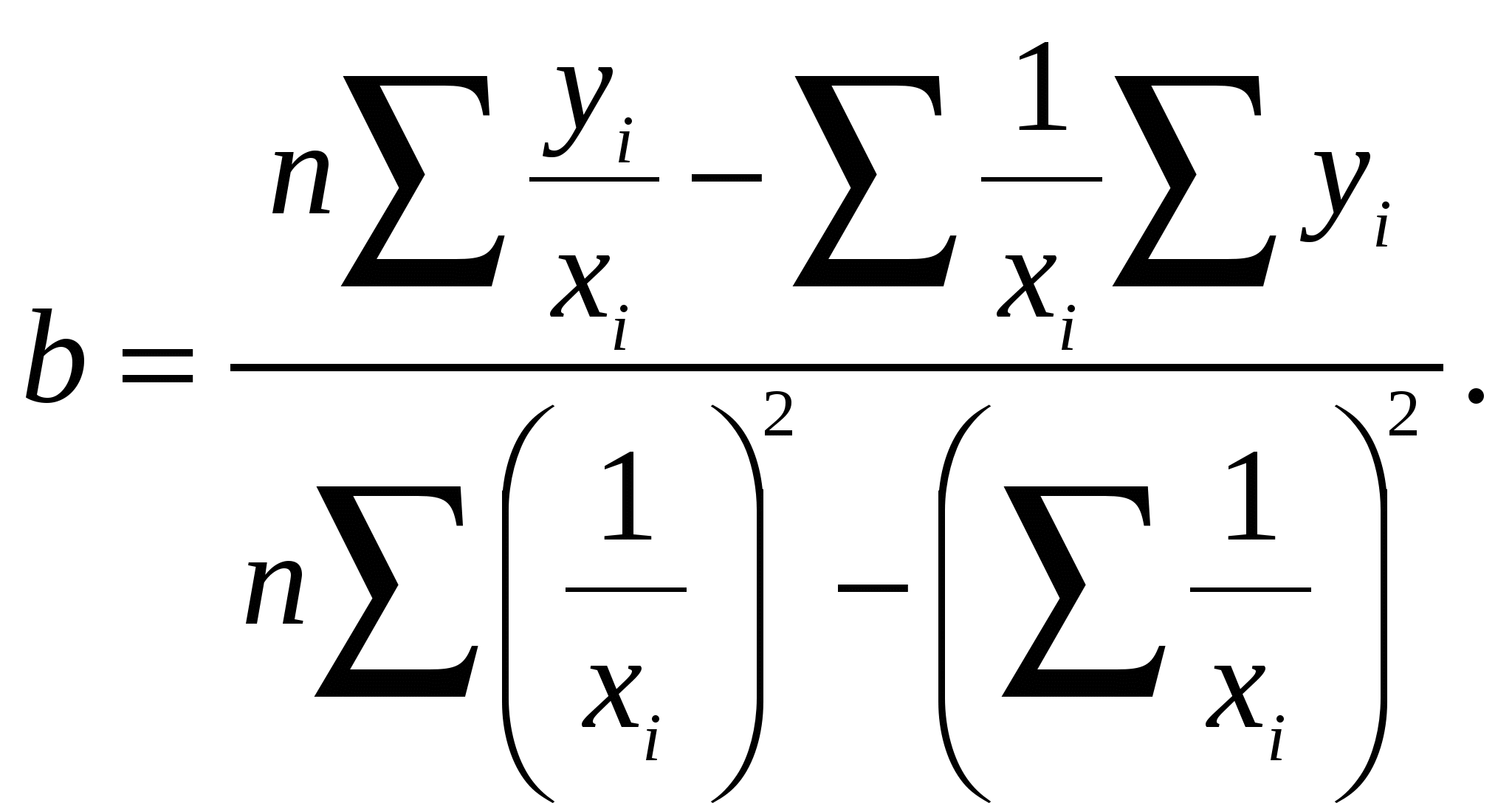





Расчет вспомогательных величин для нахождения коэффициентов уравнения приведен в таблице 1.8.2.
Таблица 7.2 Расчет вспомогательных величин для нахождения коэффициентов a и b

Диаметр, xi, см	Высота, yi, м	yi2	1/xi	(1/xi)2	yi/xi	yx=30,965-197/xi	yi-yx	(yi-yx)2
1	2	3	4	5	6	7	8	9
8	9,5	90,25	0,13	0,02	1,19	6,34	3,16	9,98
12	13,4	179,56	0,08	0,01	1,12	14,54	-1,15	1,32
16	16,3	265,69	0,06	0,01	1,02	18,65	-2,35	5,53
и т.д.
360	264,2	6293,90	0,54	0,04	9,85	сумма	-0,01	53,05

Полученное уравнение регрессии имеет вид y_х = 30,965 – (197 / x_i).

Дальнейшие расчёты производятся по аналогии с пунктом 7.1. Представить графически изменение высот от диаметров (смотри уравнение гиперболы).
Статистическое заключение

По результатам регрессионного анализа можно сделать заключение, что уравнение гиперболы, представленное результатами опыта вид y_х = 30,965 – (197 / x_i) в 8,18 раза лучше описывает изменение зависимой переменной чем среднее значение аргумента.


7.3. Уравнение показательной кривой
Для вычисления коэффициентов а и в для уравнения



необходимо решить следующую систему нормальных уравнений: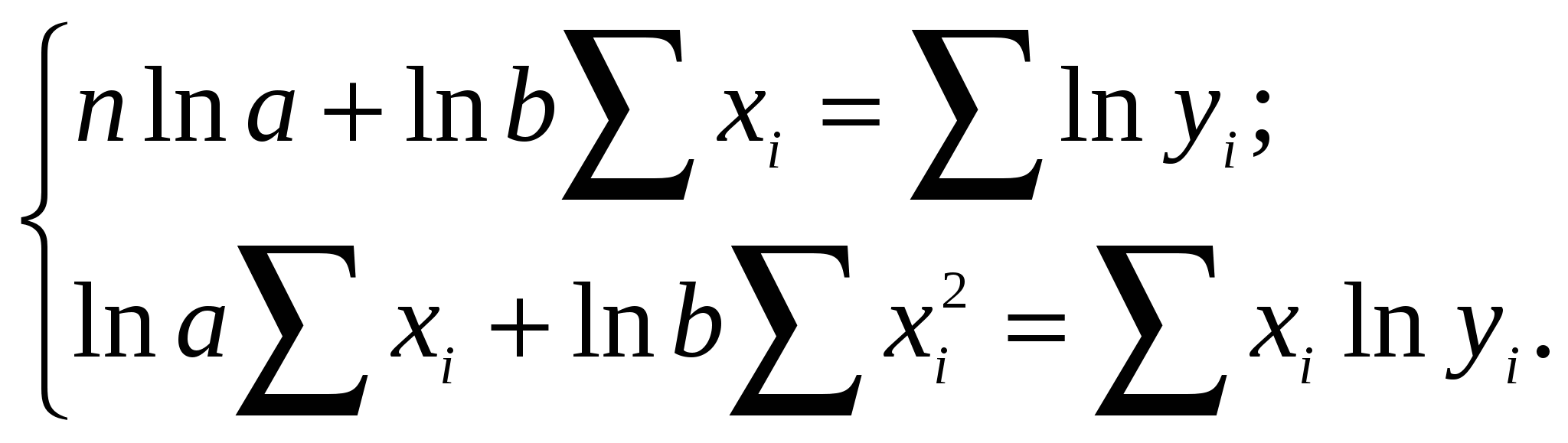



Решение системы относительно неизвестных а и в дает численные значения искомых коэффициентов: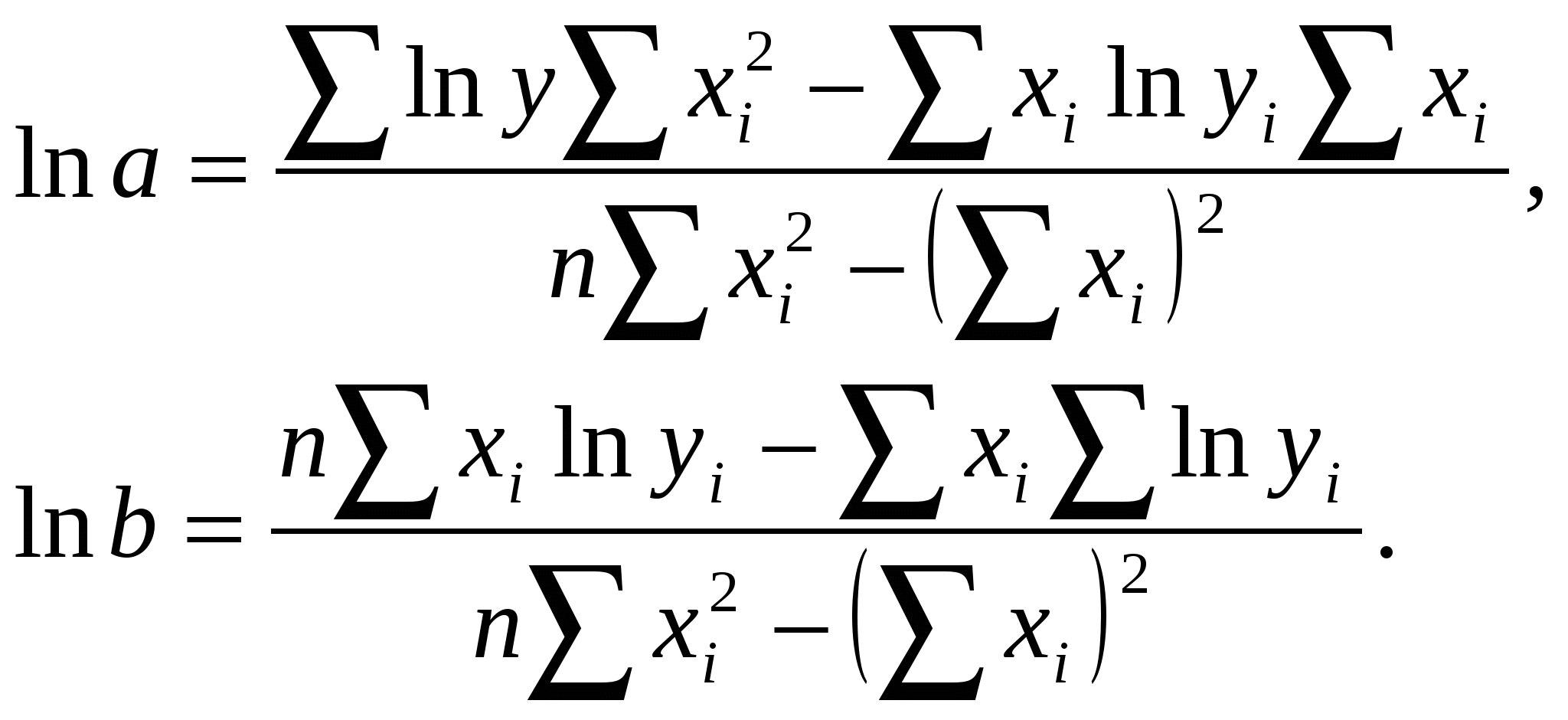



Пример: Найти уравнение регрессии, описывающее фактические значения высот по диаметрам в сосновом древостое, используя уравнение показательной кривой.

Расчет вспомогательных величин для нахождения коэффициентов уравнения приведен в таблице 7.3
Таблица 7.3 Расчет вспомогательных величин для нахождения коэффициентов а и в

Диаметр, хi,см	Высота, уi,м	xi2	yi2	lnyi,м	xilnyi	yx=10,35× ×1,024x	yi-yx	(yi-yx)2
1	2	3	4	5	6	7	8	9
8	9,5	64	90,25	2,25	18,01	12,51	-3,01	9,06
12	13,4	144	179,60	2,59	31,14	13,76	-0,36	0,13
16	16,3	256	265,70	2,79	44,66	15,13	1,17	0,37
и т.д.
360	264	13088,00	6294,00	36,59	1152,00	сумма	-2,81	69,97

Полученное уравнение регрессии имеет вид у=10,35×(1,024^х_i).

Дальнейшие расчёты производятся по аналогии с пунктом 7.1.

Представить графически изменение высот от диаметров (смотри линейное уравнение с логарифмированием факторного признака).
Статистическое заключение

По результатам регрессионного анализа можно сделать заключение, что уравнение показательной кривой, представленное результатами опыта у_х = 10,35×(1,024^х), в 6,2 раза лучше описывает изменение зависимой переменной, чем среднее значение аргумента.

4. 
   Окончательный выбор типа уравнения регрессии
   

На практике может сложиться ситуация, когда несколько уравнений адекватно предсказывают значения. В этом случае наиболее подходящим уравнением регрессии является то, которое характеризуется наибольшим фактическим значением F - критерия Фишера.

Пример. В таблице приведены три уравнения регрессии, адекватно предсказывающие значения высот по диаметрам в сосновом древостое, т. е. F_ф > F_st. Взаимное сравнение показывает, что наилучшие результаты дает уравнение регрессии, выражаемое линейным уравнением с логарифмированием факторного признака (F_ф = 109,5).

Взаимное сравнение уравнений регрессии приведено в таблице 7.4.
Таблица 7.4 Взаимное сравнение уравнений регрессии

Вид уравнения регрессии	Дисперсия		F - критерий
	Общая	Остаточная	Fф	Fst
y = 30,965 – 197 / x	43,38	5,30	8,18	2,85
yх = -14,69 + 11,42×ln xi		0,78	55,53
у = 10,35 × 1,024х		6,70	6,20

При выборе уравнения регрессии следует оперировать погрешностями и ошибками, рассчитываемыми по следующим формулам:

абсолютная погрешность уравнения



относительная погрешность уравнения



систематическая ошибка



случайная ошибка



где n – число наблюдений; y_i – значение функции по уравнению; y_x - фактическое значение функции.

Чем меньше величина погрешностей и ошибок, тем надежнее уравнение описывает исследуемую взаимосвязь.


Библиографический список

1. 
   Герасимов Ю.Ю., Хлюстов В.К. Математические методы и модели в расчетах на ЭВМ. Применение в лесоуправлении и экологии: Учебник для лесных вузов.-М.: МГУЛ, 2001. - 260 с.
   
2. 
   Доспехов Б.А. Методика полевого опыта (с основами статистической обработки результатов исследований).- 5-е изд., доп. и перераб.- М.: Агропромиздат, 1985. - 351 с.
   
3. 
   Зайцев Г.Н. Математическая статистика в экспериментальной ботанике.- М.: Наука, 1984. - 424 с.
   
4. 
   Лакин Г.Ф. Биометрия. М.: Высшая школа, 1990.-352 с.
   
5. 
   Митропольский А.К. Техника статистических вычислений.- М.: Наука, 1971. - 576 с.
   
6. 
   Фалалеев Э.Н., Смольянов А.С. Математическая статистика: Учебное пособие.- Красноярск: КГУ, 1981. - 128 с.
   

Приложения

Вопросы для контрольной работы

1. 
   Назовите основные характеристики эмпирических совокупностей и особенности их формирования.
   
2. 
   Дать определения и пояснить суть следующих терминов:
   

- размах варьирования

- дисперсия

- коэффициенты вариации и дифференциации

- стандартное отклонение

3. 
   Дать статистическую характеристику и графическое изображение кривой нормального распределения.
   
4. 
   Охарактеризуйте статистически меру скошенности и крутизны радов распределения частот.
   
5. 
   В чём заключается сущность закона нормального распределения случайной величины?
   
6. 
   Изложите методически приёмы аппроксимации рядов распределения случайной величины.
   
7. 
   Изложите особенности логнормального распределения случайной величины.
   
8. 
   Опишите статистически модели гамма и бета – распределения случайной величины.
   
9. 
   Изложите методику расчета теоретических частот по функции распределения Пуассона.
   
10. 
    Изложите методику расчета теоретических частот по типам кривых распределения Джонсона и Пирсона.
    
11. 
    В чём заключается сущность параметрической и непараметрической гипотезы?
    
12. 
    Каким статистическим критерием и как пользоваться при отнесении конкретной варианты к данной выборочной совокупности?
    
13. 
    Каким статистическим критерием и как пользоваться при оценке соответствия эмпирического распределения теоретическому?
    
14. 
    Как доказать принадлежность эмпирической совокупности к генеральной?
    
15. 
    Изложите общий подход доказательства нулевой гипотезы в лесном хозяйстве по t и F критериям.
    
16. 
    Изложите методику сравнения взвешенных рядов по критерию λ- Колмогорова-Смирнова.
    
17. 
    В чём заключается сущность дисперсионного анализа?
    
18. 
    Охарактеризуйте виды статистических комплексов, используемых в дисперсионном анализе.
    
19. 
    Приведите схемы подготовки опытных материалов к расчётам однофакторных и двухфакторных комплексов.
    
20. 
    Приведите примеры статистического доказательства существенности влияния независимых переменных на результативный признак.
    
21. 
    Охарактеризуйте функциональные и коррелятивные взаимосвязи с позиций изменения зависимой и независимой переменной. Приведите примеры выше названных взаимосвязей.
    
22. 
    Приведите примеры проведения корреляционного анализа с построением корреляционной решётки.
    
23. 
    Охарактеризуйте статистически показатели, отражающие тесноту связи между признаками.
    
24. 
    Может ли значение коэффициента корреляции превышать значение корреляционного отношения, в каких соотношениях они могу находиться?
    
25. 
    Какие статистические показатели и критерии используются для выявления прямолинейности взаимосвязи между признаками?
    
26. 
    В чём заключается сущность регрессионного анализа?
    
27. 
    Дайте определения следующим показателям центральной тенденции:
    
    • 
      мода
      
    • 
      медиана.
      

Дать статистическую характеристику.

28. 
    Приведите примеры применения вариационной статистики в лесном хозяйстве.
    
29. 
    Дать определение достоверности статистических показателей. Пояснить статистически.
    
30. 
    Дать статистическое определение следующих терминов:
    
    • 
      уровни значимости
      
    • 
      уровни доверительной вероятности (на примере кривой нормального распределения)
      
    • 
      число степеней свободы.
      
31. 
    Назвать важнейшие методические требования к полевому опыту.
    
32. 
    Назвать основные элементы методики полевого опыта.
    
33. 
    Перечислите виды ошибок, возникающих при сборе опытного материала, и их свойства.
    
34. 
    Дать определения и пояснить суть следующих терминов:
    
    • 
      совокупность
      
    • 
      переменная
      
    • 
      случайная величина.
      
35. 
    Дать определения и пояснить суть термина- вероятность события.
    

Перечислить основные теоремы теории вероятности.

36. 
    Представьте формулу расчёта необходимого числа наблюдений для будущих исследований.
    
37. 
    Дать статистическую характеристику доверительному интервалу для генеральной средней.
    
38. 
    Дайте объяснение следующему термину-«аппроксимация распределения».
    
39. 
    Виды статистических гипотез и критериев. Их практическое применение.
    
40. 
    Виды совокупностей опытных данных. Способы формирования выборок.
    
41. 
    Перечислите статистические показатели, которые характеризуют изменчивость (варьирование) изучаемого признака. Дайте статистическое определение каждого показателя.
    
42. 
    Регрессионный анализ. Методы определения значений численных коэффициентов уравнений взаимосвязи между признаками. Оценка точности уравнения регрессии.
    
43. 
    Дайте объяснение следующим терминам:
    
    • 
      результативный признак
      
    • 
      градация факторов
      
    • 
      варианты опыта
      
    • 
      повторения
      
    • 
      однофакторные и многофакторные статистические комплексы.
      
44. 
    Кривые распределения. Графическое представление вариационных рядов.
    
45. 
    Приведите общий подход определения теоретических частот эмпирического ряда распределения признака.
    
46. 
    Приведите градацию тесноты связи между признаками по значениям показателей тесноты связи.
    
47. 
    Приведите схему полного корреляционного анализа.
    
48. 
    Приведите на примере схематическое построение вариационных рядов.
    
49. 
    Изложите общий подход доказательства нулевой гипотезы в лесном хозяйстве по F –критерию. Укажите виды статистических анализов где используется данный критерий.
    
50. 
    Дать статистическую характеристику и графическое изображение кривой нормального распределения и на её примере дать определения следующих терминов:
    
    • 
      уровни доверительной вероятности
      
    • 
      уровни значимости.
      

Задачи для контрольной работы

1. 
   Указать тесноту, направление и форму взаимосвязи между диаметром ствола и его объемом, если известны следующие показатели:
   

r = + 0.923 η = 0.978

t _факт =10.2 t_факт = 13.34

t₀₅ = ? t₀₅ = ?

Число наблюдений равно 30 деревьям.

2. 
   Установить значимость различий между двумя средними, если имеем следующие данные:
   
   • 
     объемы выборок равны 20
     
   • 
     t – критерий расчетный 3.15 (t_р =3.15)
     
   • 
     t₀₅ = ? t₀₁ = ?
     
3. 
   Согласны ли Вы с заключением, что взаимосвязь между количеством осадков и урожайностью грибов по направлению прямая, по форме близка к криволинейной, по тесноте слабая, если при расчетах получили следующие данные:
   

r = 0.00 η = 0.99

4. 
   Указать направление, тесноту и форму взаимосвязи между диаметром и высотой ствола, имея расчетные показатели:
   

r = +0.96 η = 0.98

5. 
   Значима ли корреляция между диаметром ствола и количеством шишек, если получены следующие показатели:
   

r = - 0.71 η = 0.81 t₀₅ = 2.045

m_r = 0.02 m_r = 0.09

n = 30(объем выборки)

6. 
   Указать существенные или несущественные различия между сравниваемыми классами бонитета по продуктивности древостоев, если получили следующие показатели по дисперсионному анализу:
   

F_расч = 28 F_05/01 =2.62/3.9

7. 
   Оцените работу двух таксаторов, если при вычислении среднеквадратических ошибок получили такие данные:
   

I таксатор II таксатор

Случайная ошибка σ₁ =8.17% σ₂ = 10.12%