Новая методичка статистика. 1 Расчёт основных статистических показателей для выборочных совокупностей

• Название: 1 Расчёт основных статистических показателей для выборочных совокупностей
• Дата: 16.02.2018
• Размер: 1.22 Mb.
• Имя файла: Новая методичка статистика.doc
• Тип: Документы; #36650
• страница: 2 из 11

Статистическое заключение
В результате анализа малой выборочной совокупности в виде измерения диаметра деревьев на высоте 1,3 м в сосновом древостое получили следующие статистические показатели с их ошибками репрезентативности:

- средняя арифметическая величина 31,08 ± 0,85 см;

- стандартное отклонение (среднее квадратичное отклонение) 4,67 ± 0,60 см;

- коэффициент вариации 15,03 ± 1,98 % , которому по шкале Мамаева соответствует низкий уровень изменчивости;

- коэффициент дифференциации 65,96 %, которому по классификации соответствует большая степень дифференциации.

Точность опыта 2,73± 0,36 %, по которой можно сделать вывод о том, что процент расхождения между генеральной и выборочной средней невелик. Следовательно по выборке можно сделать достоверное заключение о все совокупности в целом.

Все статистические показатели достоверны, т. к. их отношение к ошибкам репрезентативности больше 3 во всех случаях.

Доверительный интервал генеральной средней 29,34 ÷ 32,82 см. Расстояние между точками интервала невелико, следовательно выборочная совокупность достаточно точнее характеризует генеральные параметры.

Необходимое число наблюдений для будущих исследований, которое бы обеспечивало заданную точность 2% при известном коэффициенте вариации 15,03 % и трех пороговых уровнях доверительной вероятности следующее:

- для 1^го порогового уровня 64 штук;

- для 2^го порогового уровня 225 штук;

- для 3^го порогового уровня 400 штук.

1.2. Большая выборочная совокупность
Большая выборочная совокупность – это совокупность, объем которой более 30 вариант.

Когда имеем дело с большой выборочной совокупностью, необходимо все полученные данные упорядочить в порядке возрастания или убывания. При этом строится вариационный ряд.

Вариационный ряд - это размещение значений признака в порядке возрастания или убывания с указанием числа их повторяемости (ранжированный ряд данных). В вариационном ряду значения признака разносятся по классам. В результате получают ранжированный ряд данных. Каждая группа вариант, на которое разбивается выборочная совокупность, называется классом. Число вариант, относящихся к данному классу, называют его частотой (классовой частотой). Сумма всех частот составляет объем выборки (n). Вариационный ряд составляется для получения основных статистических показателей, а так же для определения типа распределения по изучаемому признаку.

Данные большой выборочной совокупности приведены в таблице 1.4.
Таблица 1.4 - Данные для статистической обработки большой выборочной

совокупности

	I	II	III	IV	V	VI	VII	VIII	IX	X
1	6,00	12,60	8,40	20,60	36,00	22,00	16,00	16,00	21,00	18,80
2	18,60	32,00	22,00	28,50	26,00	24,00	38,00	20,60	24,00	26,00
3	13,80	20,00	32,40	21,80	14,60	18,00	26,00	29,40	16,40	21,60
4	36,00	34,00	31,80	29,30	24,60	24,60	19,00	24,00	23,60	22,90
5	34,60	30,80	30,00	26,00	36,40	24,00	24,00	23,80	38,60	20,80
6	12,00	30,00	28,00	15,60	24,00	25,00	13,40	26,80	23,40	26,00
7	26,60	40,40	29,40	24,00	21,80	42,00	22,40	33,00	24,00	35,60
8	32,40	27,50	34,00	44,60	23,60	23,60	28,00	23,40	46,00	20,00
9	28,00	28,60	32,60	23,80	36,00	20,40	27,00	24,00	24,40	35,00
10	14,60	18,00	22,00	25,00	18,00	25,80	28,60	22,00	31,80	14,60

1.2.1 Схематическое представление вариационного ряда
Для построения вариационного ряда необходимо выполнить следующие действия:

1. 
   Выбрать x_min и x_max
   

Например:

x_min = 6 см.; x_max = 46 см.
Установить размах варьирования:

Например:

x_max – x_min = 46 – 6 = 40 см.

2. 
   Определить классовый интервал:
   

(1),

где x_max – максимальное значение варианты; x_min – минимальное значение варианты; i– количество классов.

В математической статистике существуют придержки для установления количества классов в зависимости от объёма совокупности:

- если объем выборочной совокупности до 100 вариантов, то количество классов от 6 до 9;

- если более 100 вариантов, то количество классов от 9 – 12.

Количество классов можно рассчитывают по формуле:

где n– объем выборочной совокупности.

Заданное количество классов в курсовой работе равно 10.

Например: величина классового интервала будет равна:

C = 46 – 6 / 10 = 4 см.

В некоторых случаях для установления величины классового интервала (промежутка) можно использовать формулу Стерджеса, которая имеет следующий вид:

, (2)

В курсовой работе величину классового интервала рассчитать по формуле (1).

3. 
   Установить границы классов, то есть начало и окончание классов.
   

В практике чаще всего границы классов определяются следующим образом:

За начало (нижняя граница) принимаютx_min

За окончание (верхняя граница) считается величина равная x_min+ C

Например:

Нижняя граница: х_н= x_min = 6 см.

Верхняя граница: х_в= x_min+ C = 6 + 4 = 10 см.

В некоторых случаях границы классов можно определить и так:

Нижняя граница: х_н= x_mi - C

2

Верхняя граница: х_в= x_min+ C

2

Например:

Нижняя граница: х_н= x_mi - C =6 - 4=4 см

2 2

Верхняя граница: х_в= x_min+ C =6 + 4=8 см

2 2

Вычисленные границы классов представлены в таблице 1.5.
Таблица 1.5 Границы классов

Классы	Границы классов
I	6,0 – 10,0
II	10,1 – 14,0
III	14,1 – 18,0
IV	18,1 – 22,0
V	22,1 – 26,0
VI	26,1 – 30,0
VII	30,1 – 34,0
VIII	34,1 – 38,0
IX	38,1 – 42,0
X	42,1 – 46,0

После установления границ классов приступают к схематическому изображению вариационного ряда.

Частота по изучаемому признаку в схематическом изображении сначала указывается «методом конвертов». Полный конверт включает в себя 10 единиц по изучаемому признаку.

Далее частота указывается арабскими цифрами и приводится расчет накопленных частот. Последнее значение по накопленной частоте при верном расчете должно быть равно объему выборочной совокупности.

Схематическое изображение вариационного ряда
Классы I II III IV V VI VII VIII IX X
Границы 6,0 – 10,0 – 14,0 – 18,0 – 22,0 – 26,0 – 30,0 – 34,0 – 38,0 – 42,0 – 46,0

классов • • • • • • • •

• • •

• • •

• • •


Частота, шт. 2 4 11 16 30 14 10 8 3 2
Накопленная 2 6 17 33 63 77 87 95 98 100

частота, шт


В курсовой работе схематическое изображение вариационного ряда представить на отдельном листе.
1.2.2. Графическое представление вариационного ряда
После того как произведена группировка совокупности по классам, характер распределения более или менее проясняется. Однако более наглядное представление закономерности варьирования изучаемого признака вариационный ряд распределения изображают в виде графиков распределения.

Существует четыре способа графического изображения вариационных рядов:

1. 
   Гистограмма.
   
2. 
   Кумулята.
   
3. 
   Огива.
   
4. 
   Полигон распределения.
   

Гистограмма
При построении гистограммы по оси абсцисс откладываются верхние и нижние границы классов, и на этих отрезках как на основаниях, строятся прямоугольники, высота которых соответствует частоте класса. По оси ординат откладываются частоты классов.

Изображение распределения при помощи гистограммы представляет собой другой крайний случай идеализации: если в случае полигона частот все значения, лежащие внутри разряда, «стягиваются» к середине разряда, то в случае гистограммы они считаются распределенными равномерно по всему разряду. Площадь, ограниченная гистограммой, пропорциональна объему совокупности.
Например:



Кумулята

(кривая накопленных частот)
Для построения кумуляты по оси абсцисс откладывают границы классов, а по оси ординат – накопленную частоту класса. Точки на график наносятся в соответствии с верхней границей класса и его накопленной частотой. Начало кумуляты в нижней границе первого класса.

Например: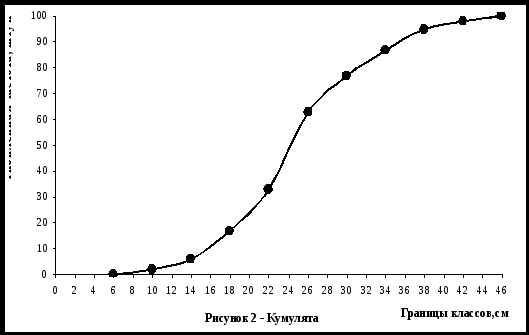