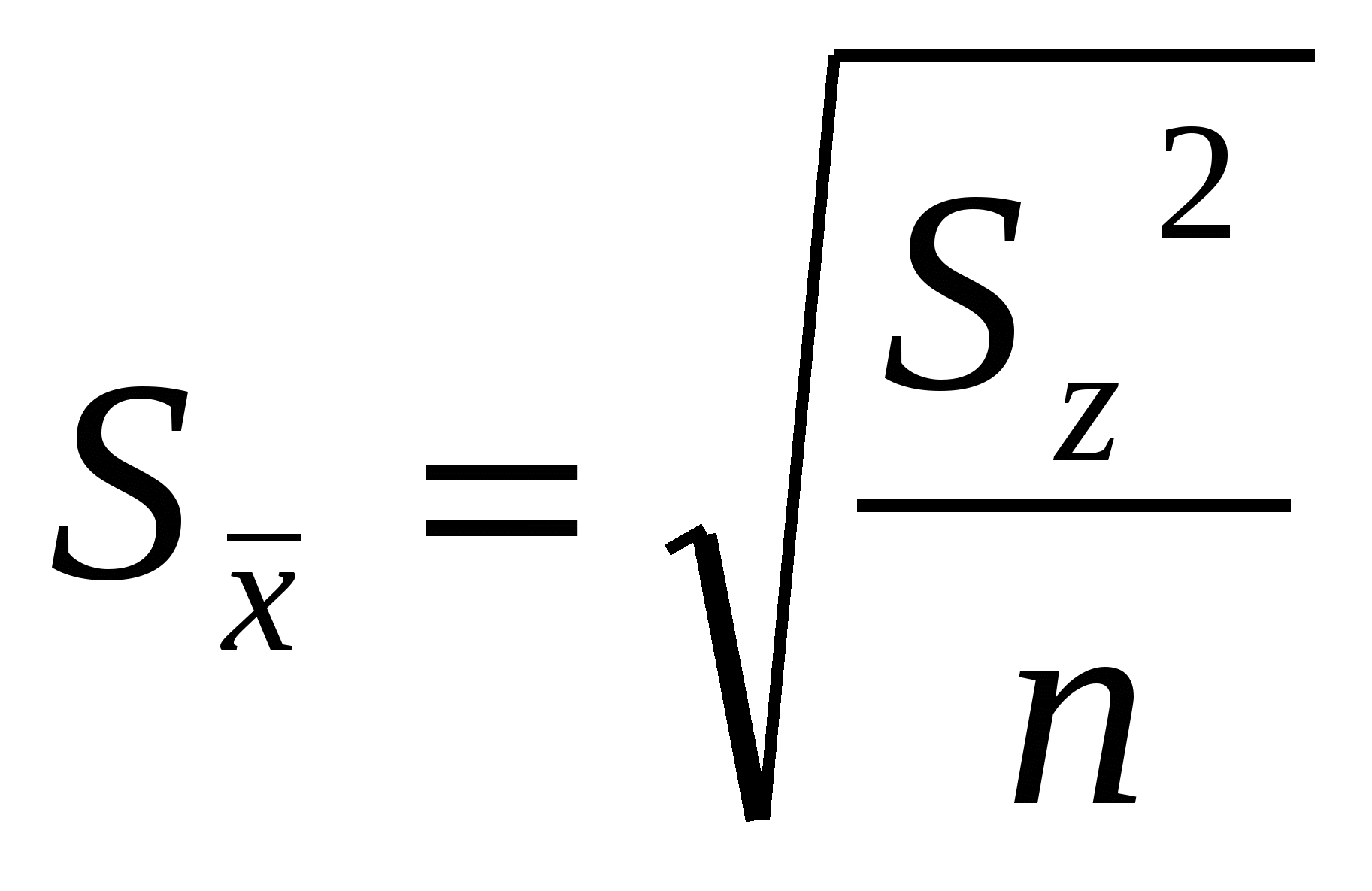Новая методичка статистика. 1 Расчёт основных статистических показателей для выборочных совокупностей
 Скачать 1.22 Mb. Скачать 1.22 Mb.
|
|
Вычисление суммы квадратов отклонений 1. Общее число наблюдений: ∑ n = N = l × n = 45 ( или 5×9 = 45). l– количество вариантов опыта (в примере 5) n – количество повторностей по варианту ( в примере 9) 2. Корректирующий фактор
Результаты вычислений представлены в таблице 5.3. Таблица 4.3 Результаты вычислений
- средний квадрат дисперсии вариантов sv2 = Cv/ (l – 1); - средний квадрат дисперсии остатка sz2 = Cz / (N – l).. - фактическое значение F-критерия Фишера FФ > F01 , следовательно, различия между сравниваемыми вариантами можно считать существенными. F05 и F01 определяют по числу степеней свободы большей дисперсии (вариантов) и по числу степеней свободы меньшей дисперсии (остатка) по приложению учебника (стр.247). Так как различия существенны, необходимо произвести оценку по наименьшей существенной разности (НСР05). Чтобы определить НСР необходимо по данным дисперсионного анализа вычислить обобщенную ошибку средней величины по опыту и ошибку разности средних.
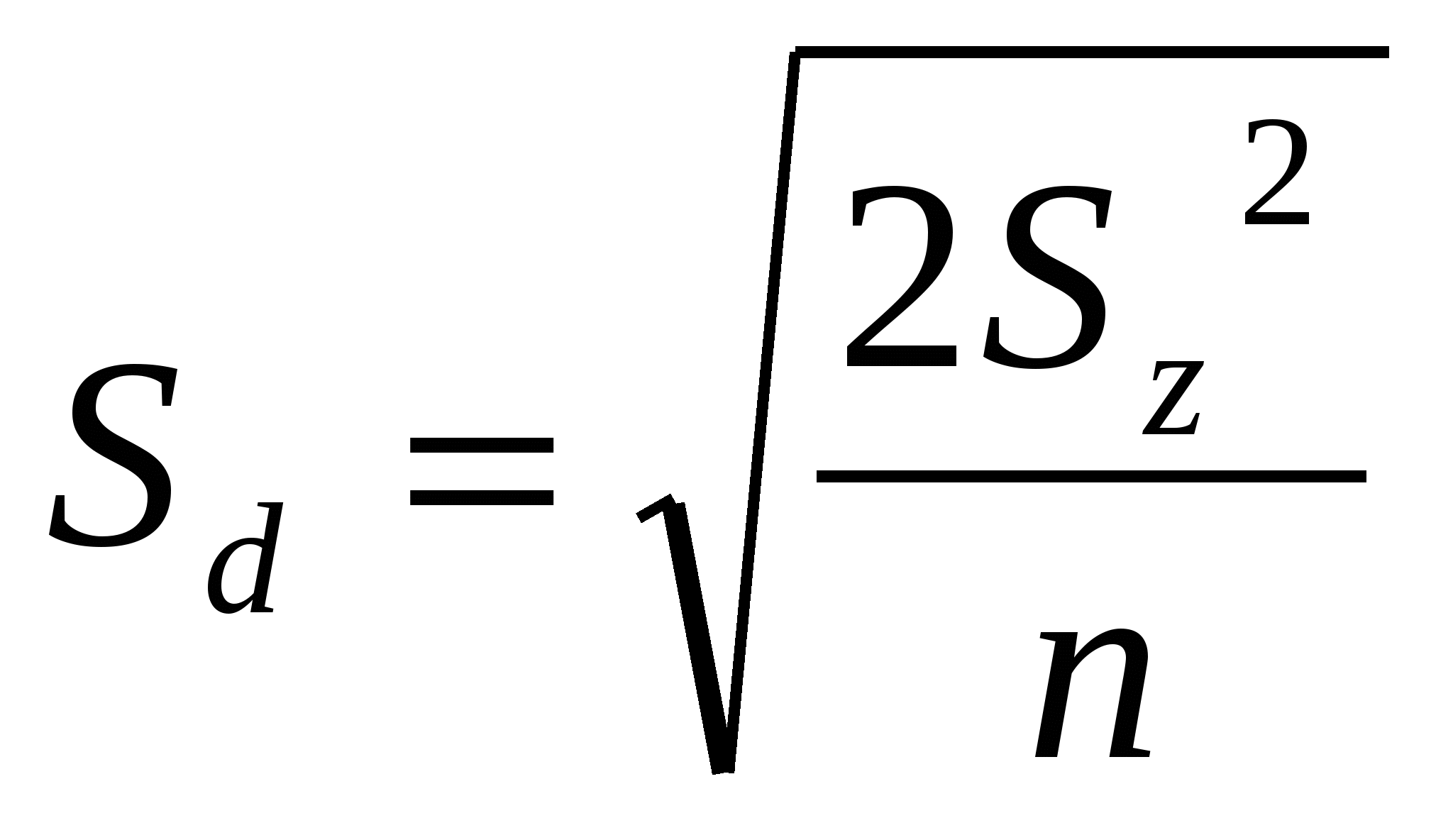 . .
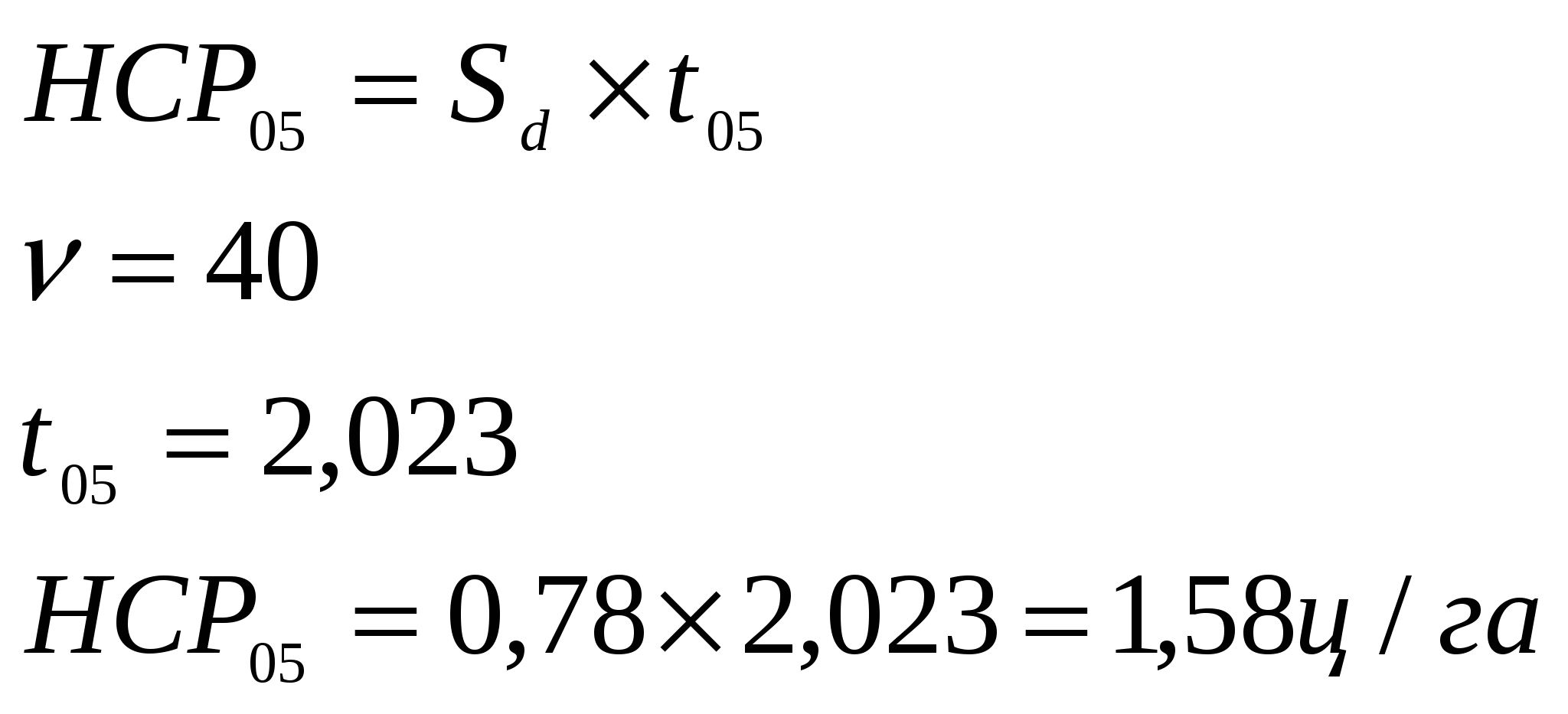 t критерий Стьюдента на 5 % уровне значимости берётся по числу степеней свободы дисперсии остатка 4. Критерий НСР выраженный в единицах выраженный в единицах 5. Определение места в ряду распределения приведено в таблице 4.4. Таблица 4.4 Итог результатов опыта
Для определения места в ряду распределения необходимо найти разность со стандартом. За стандарт берется тот вариант, который рекомендуется использовать в данных условиях, либо который уже внедрен в производство. Место в ряду распределения отводится только тем вариантам, фактическая разность со стандартом у которых превышает значение НСР05. Статистическое заключение По результатам дисперсионного анализа можно сделать заключение, что различия между сравниваемыми вариантами существенные, т.к. фактическое значение F критерия Фишера больше F критерия на 5 и 1 % уровне значимости. Для производства рекомендуется вариант № V (сорт Нижегородская), т.к. его фактическая разность со стандартом превышает значение НСР05 (47,53 >5,83). 5. Корреляционный анализ Отличительной чертой лесохозяйственных объектов является многообразие признаков, характеризующих каждый из них. Так, дерево можно характеризовать возрастом, размерами, объемом и т. д. Чем больше размеры дерева, тем обычно больше объем его стволовой части. Существуют функциональные и коррелятивные зависимости. Функциональные - это зависимости, при которых каждому конкретному значению независимой переменной (х) соответствует строго определенное значение зависимой переменной (y). Коррелятивной зависимостью называют зависимость, при которой каждому конкретному значению независимой соответствует множество значений зависимой переменной. При выявлении корреляционной зависимости могут иметь место тренды различной направленности. Если с увеличением независимой переменной зависимая увеличивается, то зависимость называют прямой корреляционной зависимостью. Есть случаи, когда с увеличением независимой переменной зависимая уменьшается. В этом случае зависимость называется обратной корреляционной зависимостью. Корреляционный анализ имеет своей задачей количественное определение тесноты связей между признаками при парной связи и между результативным (изменяющемся под действием других, связанных с ним признаков) и множеством факторных признаков (обуславливающих изменения результативных признаков) при многофакторной связи. Теснота связи количественно выражается величиной коэффициентов корреляции. Корреляционная зависимость характеризует лишь прямолинейное изменение. Коэффициент корреляции может принимать значения от - 1 до + 1. При полной прямой корреляции r = + 1, при полной обратной корреляции r = - 1. При r = 0 прямолинейная связь отсутствует (криволинейная связь при этом может наблюдаться). где N – число наблюдений; Sx , Sy – средние квадратические отклонения распределений x и y. Для определения значимости коэффициента корреляции необходимо рассчитать его ошибку: Значимость r (коэффициента корреляции) определяется отношением: Вычисленный tr сравнивается с t – критерием на пяти- и однопроцентном уровне значимости при числе степеней свободы ν = n – 2, где n - объем выборки. Если tр > t05, то зависимость существенная. А если tp < t05, то зависимость отсутствует. Корреляционное отношение – это градация тесноты взаимосвязей по значению r. Наличие криволинейной связи оценивается по корреляционному отношению (η). Вычисляется корреляционное отношение как отношение среднего квадратического отклонения групповых средних Syx к общему среднему квадратическому отклонению Sy. где My – общее среднее арифметическое; Myi - групповое среднее арифметическое; fi – частота ряда x. Корреляционное отношение показывает, какую часть общей вариации результативного признака составляет вариация частных средних этого признака. Корреляционное отношение имеет всегда положительное значение, изменяющееся от 0 до 1. Когда групповые средние одинаковы, то η = 0 и связь отсутствует. В случае строгой прямолинейной связи (все точки лежат на одной прямой) η = r = 1. Чем ближе η к 1, тем связь теснее. Чем больше различие между η и r, тем связь более криволинейна. В предельном случае, когда связь строго криволинейна и кривая проходит через групповые средние так, что Syx = Sy, то η = 1, а r = 0. Значимость корреляционного отношения определяется через ошибку корреляционного отношения В заключение tр сравнивается с t табличным на пяти- и однопроцентном уровне значимости. Если tр > t05, то нулевую гипотезу отвергают на принятом уровне значимости. Схема полного корреляционного анализа Если при обработке информации возникает задача установления связи между двумя величинами, то работу проводят в определенной последовательности: - на график наносят значения пар (xi, yi) для визуальной оценки наличия и тесноты связи; - если связь явно нелинейная, то вычисляют и оценивают корреляционное отношение η; - если определенного заключения по графику сделать нельзя, то наряду с корреляционным отношением η вычисляют коэффициент корреляции r, после чего вычисляется мера линейности ε и ее основная ошибка mε : Величина меры линейности характеризует отклонение связи от прямолинейной. Если ε / mε > 2, то гипотезу о нелинейности связи принимают, в противном случае (ε / mε < 2) связь приближенно можно считать линейной. Для более точной оценки наличия криволинейности взаимосвязи пользуются F - критерием линейности корреляции, который сравнивается с табличным при уровнях значимости α = 0, 05 и α = 0,01 при К1 = Кх – 2 и К2 = n – 2 степенях свободы. Fр =( ( η2 – r2 ) × ( n – Кx ) ) где η2 – квадрат корреляционного отношения y по x; r2 – квадрат линейной корреляции; n – объем выборки; Кx – число групп по ряду х. Гипотеза о прямолинейности взаимосвязи отвергается, если Fр > Fт при уровне значимости α = 0,01 и принимается, если Fр < Fт при α = 0,05. В природных, биологических объектах во всем диапазоне закономерных изменений зависимой переменной от независимой, как правило, проявляется криволинейность. 5.1. Расчё показателей корреляции на примере малой выборочной совокупности Расчет вспомогательных величин для вычисления коэффициента корреляции приведен в таблице 5.1. Таблица 5.1 Расчет вспомогательных величин для коэффициента корреляции
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||