Изучение наглядной геометрии в 5-6 классах. Диплом. 1. Теоретические основы проблемы геометрической пропедевтики в математическом образовании Из истории решения проблемы геометрической пропедевтики в математическом образовании

Название	1. Теоретические основы проблемы геометрической пропедевтики в математическом образовании Из истории решения проблемы геометрической пропедевтики в математическом образовании
Анкор	Изучение наглядной геометрии в 5-6 классах
Дата	29.03.2022
Размер	0.76 Mb.
Формат файла
Имя файла	Диплом.docx
Тип	Исследование #425430
страница	7 из 8

1 2 3 4 5 6 7 8

2.4. Анализ результатов опытно-экспериментальной работы по проблеме исследования

В качестве гипотезы исследования выступило предположение о том, что если через организацию поисково-эвристической деятельности изучать геометрические понятия у младших школьников, то это будет способствовать успешному обучению.

С целью проверки выдвинутой нами гипотезы, нами была организована и проведена опытно-экспериментальная работа с учащимися 5 «Б» и 5 «Г» классов МБОУ РО г.Шахты «Лицей №6» в рамках внеурочной деятельности «Математика после уроков». Данные классы занимаются по программе УМК «Школа России». В каждом классе обучается 20 человек.

Первым этапом опытно-экспериментальной работы явилась первоначальная диагностика учащихся. Для этого нами были разработаны и предложены определенные задания, с помощью которых мы выявим уровень знаний по теме исследования.

Первым заданием школьникам предложено определить и подписать фигуры, которые они видят на рисунке.

Задание 1. Какие геометрические фигуры ты видишь? Подпиши их названия.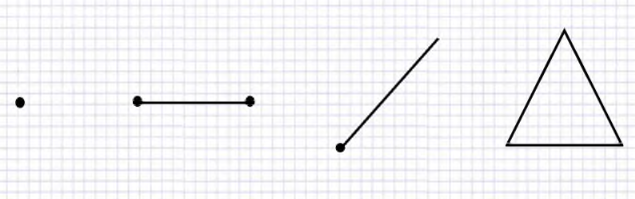

Во втором задании школьникам необходимо, зная свойства фигур, сделать построение согласно заданным условиям.

Задание 2. Какой угол называется прямым? Какие геометрические фигуры с прямым углом ты знаешь? Нарисуй их.

Третье задание направленно на работу ученика с таким измерительным прибором, как линейка. Необходимо измерить отрезок.

Задание 3. Измерь отрезок. Запиши результат измерения:

В четвертом задании школьнику нужно определить недостающую фигуру, по каким-либо признакам и дорисовать ее.

Задание 4. Дорисуй недостающую фигуру: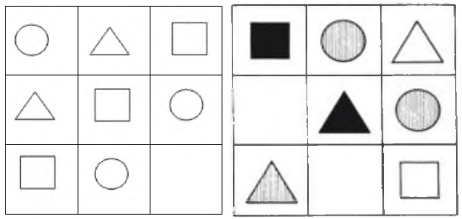

Задание 5. Вычисли значения величин:

25 дм 5 см = __см__мм = ___мм

4 м 8 дм = __дм = ___см

360 см = ___ дм = ___мм

Задание 6. Продолжи определения и зарисуй

Прямой угол – это_____________________________________________.

Тупой угол – это______________________________________________.

Острый угол – это__________________________________________.

Задание 7. Реши задачу: Сумма длин сторон квадрата равна 40 см. Чему равна длина каждой его стороны?

Задание 8. Реши задачу: Длина прямоугольника 11 дм, это на 6 дм больше, чем ширина. Найди длину квадрата с тем же периметром.

Задание 9. Реши задачу: Длина прямоугольника 13 см, это на 7 см больше ширины. Найдите площадь и периметр прямоугольника

Задание 10. Реши задачу: Периметр прямоугольника равен 36 см, длина 12 см. Найдите площадь прямоугольника.

И последним заданием необходимо выполнить анализ своей деятельности.

Задание 11. Проанализируй свой результат. Что у тебя получилось, а что нет.

После выполнения учащимися вышеприведенных заданий (задач, геометрических построений), детские работы были нами проверены и обработаны по специально подобранным критериям. В качестве критериев нами были выбраны:

1.Находить названную геометрическую фигуру среди других и называть ее свойства;

2.Владение элементарными способами построения и использовать сочетания данных способов при выполнении геометрических фигур;

3.Умение сравнивать геометрические фигуры по величине и свойствам;

4.Умение ребенком правильно представить последовательность действий, направленных на получение конечного результата;

5.Умение ребенком осуществлять рефлексию своей деятельности, самостоятельная проверка правильности построения.

Критерии оцениваются по следующим показателям:

2 - достаточно полное проявление показателя для выделенного критерия;

1 - частичное проявление выделенного критерия;

0 - отсутствие или низкая степень проявления критерия в работе учащегося.

Все показатели, которые мы получили, в ходе первичной проверки были занесены в таблицу 1 и 2.

Таблица 1 - Результаты первичной диагностики формирования у школьников экспериментальной группы геометрических понятий (5 «Б»)

№ п/п	ФИ	Критерии						Кол-во баллов
№ п/п	ФИ	1	2	3	4	5		Кол-во баллов
1	А.И.	1	1	1	1	0	4
2	А.Н.	2	2	2	2	1	9
3	В.Г.	1	2	1	2	0	6
4	Г.Д.	1	0	1	0	0	2
5	Д.О.	1	2	2	1	1	7
6	Д.Н.	1	2	1	1	1	6
7	И.Н.	1	2	1	2	0	6
8	К.А.	2	2	2	2	1	9
9	Л.Н.	1	2	1	1	1	6
10	М.Е.	1	1	1	0	0	3
11	М.Ю.	1	2	2	1	1	7
12	Н.В.	1	2	1	2	0	6
13	Н.Н.	2	2	2	2	1	9
14	О.В.	1	2	2	1	1	7
15	О.Л.	1	2	1	2	0	6
16	О.Н.	1	0	1	1	0	3
17	П.Л.	1	2	1	2	1	7
18	Р.А.	1	2	1	1	1	6
19	С.А.	1	1	1	1	0	4
20	Т.Е.	1	2	1	2	0	6

Таблица 2 - Результаты первичной диагностики формирования у школьников контрольной группы геометрических понятий (5 «Г»)

№ п/п	ФИ	Критерии						Кол-во баллов
№ п/п	ФИ	1	2	3	4	5		Кол-во баллов
1	А.В.	1	1	1	1	0	4
2	Б.И.	1	2	1	2	0	6
3	В.И.	2	2	2	2	1	9
4	Д.Н.	2	1	1	2	1	7
5	З.Ю.	2	1	1	2	0	6
6	И.А.	2	2	2	2	1	9
7	И.Н.	1	0	1	1	0	3
8	К.Н.	1	2	1	2	0	6
9	К.О.	2	1	2	1	1	7
10	Л.О.	1	1	1	1	0	4
11	М.А.	1	1	2	2	1	7
12	М.И.	1	1	1	0	0	3
13	Н.О.	2	2	1	1	0	6
14	Н.Р.	2	2	2	2	1	9
15	О.Н.	1	2	1	2	0	6
16	П.Р.	1	1	1	1	0	4
17	Р.С.	2	2	1	1	0	7
18	С.К.	2	2	2	2	1	9
19	С.Л.	1	1	0	1	0	3
20	С.Н.	2	1	1	1	0	5

Для адаптации к особенностям настоящего исследования балльная система была переведена в трехуровневую следующим образом:
Таблица 3 - Показатели уровня формирования у школьников геометрических понятий

% результативности (балл по критериям)	Качественная оценка балл (отметка)	Вербальный аналог (уровень)
9-10 баллов	90-100%	Высокий
6-8 баллов	60-80%	Средний
5 и менее баллов	50% и менее	Низкий

Сравнительный анализ уровня развития формирования геометрических понятий у детей ЭГ и КГ на констатирующем этапе эмпирического исследования представлен в таблице 4 и на рисунке 1.
Таблица 4 - Сравнительная таблица уровней формирования геометрических понятий у детей КГ и ЭГ на констатирующем этапе эксперимента (в %)

Уровень развития умения	Экспериментальная группа n=20		Контрольная группа n=20		φ - критерий Фишера в сравнении с ЭГ
Уровень развития умения	Кол-во детей	% соотношение	Кол-во детей	% соотношение	φ - критерий Фишера в сравнении с ЭГ
Высокий уровень	3	15%	4	20%	0,417
Средний уровень	12	60%	10	50%	0,636
Низкий уровень	5	25%	6	30%	0,354

Примечание:

* - различия статистически значимы при φ_кр =1,64 для р≤ 0,05;

** - различия статистически значимы при φ_кр=2,31 для р≤ 0,01;

*** - различия статистически значимы при φ_кр =2,81 для р≤ 0,001.

Анализ результатов констатирующего этапа эмпирического исследования в ЭГ и КГ показал, что значимых различий в уровне формирования геометрических понятий у детей ЭГ и КГ нет. В обеих группах преобладают дети со средним уровнем формирования геометрических понятий: 60% детей в – ЭГ и 50% детей - в КГ. Высокий уровень формирования геометрических понятий выявлен у 15% детей ЭГ и у 20% детей КГ. Низкий уровень формирования геометрических понятий в экспериментальной группе обнаружен у 25% детей, а в контрольной группе – у 30% детей.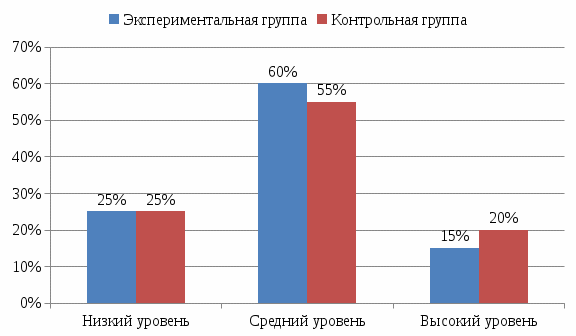

Рисунок 1 - Сравнительная диаграмма уровня формирования геометрических понятий у детей КГ и ЭГ на констатирующем этапе эксперимента (в %)
Проведенное исследование позволило установить, в каких показателях у каждого учащегося отмечаются наибольшие затруднения и на какие моменты можно опираться в процессе дальнейшего обучения.

Анализируя результаты первичной диагностики можно констатировать, что знанием названий геометрических фигур дети владеют хорошо, однако сравнивать их и строить получается далеко не у всех. Также умение ребенком правильно представить последовательность действий, направленных на получение конечного результата развито у небольшого количества детей. Анализ своей работы выполнило всего 17 человек из 40, т.к. остальные просто не знали, что написать и что от них требуется.

С целью изменения данной ситуации нами был организован второй этап опытно-экспериментальной работы, на котором нами был апробирован курс «Наглядная геометрия» в процессе формирования у школьников геометрических понятий.

С целью проверки эффективности проведенной работы, а также с целью подведения итогов эксперимента, нами был организован третий этап опытно-экспериментальной работы - повторная диагностика учащихся.

Задания были подобранны по типу первой диагностики, с целью обеспечения чистоты эксперимента.

Итак. Первым заданием школьникам предложено определить и подписать фигуры, которые они видят на рисунке.

Задание 1. Какие геометрические фигуры ты видишь? Раздели их на две группы, и подпиши их названия.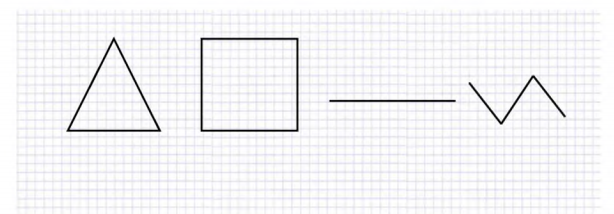

Во втором задании школьникам необходимо, зная свойства фигур, сделать построение согласно заданным условиям.

Задание 2. Нарисуй треугольник, у которого один угол прямой, а стороны прилегающие к этому углу были 7см и 5 см.

Третье задание направленно на работу ученика с таким измерительным прибором, как линейка. Необходимо измерить отрезок.

Задание 3. Измерь отрезок. Запиши результат измерения: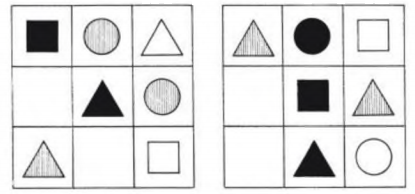

Задание 5. Вычисли значения величин:

20 дм 5 см = __см__мм = ___мм

3 м 8 дм = __дм = ___см

250 см = ___ дм = ___мм

Задание 6. Продолжи определения и зарисуй

Луч – это_____________________________________________.

Прямая – это______________________________________________.

Отрезок – это__________________________________________.

Задание 7. Реши задачу: Сумма длин сторон квадрата равна 60 см. Чему равна длина каждой его стороны?

Задание 8. Реши задачу: Длина прямоугольника 12 дм, это на 5 дм больше, чем ширина. Найди длину квадрата с тем же периметром.

Задание 9. Реши задачу: Длина прямоугольника 15 см, это на 8 см больше ширины. Найдите площадь и периметр прямоугольника

Задание 10. Реши задачу: Периметр прямоугольника равен 40 см, длина 15 см. Найдите площадь прямоугольника.

И последним заданием необходимо выполнить анализ своей деятельности.

Задание 11. Проанализируй свой результат. Что у тебя получилось, а что нет.

Как и в первой части нашей опытно - экспериментальной работы после выполнения учащимися вышеприведенных заданий (задач, геометрических построений), детские работы были нами проверены и обработаны по критериям приведенным выше.

Все показатели, которые мы получили, в ходе повторной проверки были занесены в таблицу 5 и 6.
Таблица 5 - Результаты вторичной диагностики формирования у школьников экспериментальной группы геометрических понятий (5 «Б»)

№ п/п	ФИ	Критерии						Кол-во баллов
№ п/п	ФИ	1	2	3	4	5		Кол-во баллов
1	А.И.	1	1	1	1	0	4
2	А.Н.	2	2	2	2	2	10
3	В.Г.	2	2	2	2	1	9
4	Г.Д.	1	1	1	1	1	5
5	Д.О.	2	2	2	2	1	9
6	Д.Н.	1	2	2	2	1	8
7	И.Н.	2	2	2	2	1	9
8	К.А.	2	2	2	2	2	10
9	Л.Н.	2	2	2	1	1	8
10	М.Е.	1	1	2	1	1	6
11	М.Ю.	2	2	2	2	1	9
12	Н.В.	1	2	2	2	1	8
13	Н.Н.	2	2	2	2	2	10
14	О.В.	2	2	2	2	1	9
15	О.Л.	1	2	2	2	1	8
16	О.Н.	1	2	1	1	1	6
17	П.Л.	2	2	2	2	1	9
18	Р.А.	2	2	2	2	1	9
19	С.А.	1	2	1	1	1	6
20	Т.Е.	1	2	2	2	1	8

Таблица 6 - Результаты вторичной диагностики формирования у школьников контрольной группы геометрических понятий (5 «Г»)

№ п/п	ФИ	Критерии						Кол-во баллов
№ п/п	ФИ	1	2	3	4	5		Кол-во баллов
1	А.В.	1	1	1	1	1	5
2	Б.И.	1	2	1	2	0	6
3	В.И.	2	2	2	2	1	9
4	Д.Н.	2	1	1	2	1	7
5	З.Ю.	2	1	1	2	1	7
6	И.А.	2	2	2	2	1	9
7	И.Н.	1	0	1	1	0	3
8	К.Н.	1	2	1	2	0	6
9	К.О.	2	2	2	2	1	9
10	Л.О.	1	1	1	1	1	5
11	М.А.	1	1	2	2	1	7
12	М.И.	1	1	1	1	0	4
13	Н.О.	2	2	1	1	1	7
14	Н.Р.	2	2	2	2	1	9
15	О.Н.	1	2	1	2	0	6
16	П.Р.	1	1	1	1	0	4
17	Р.С.	2	2	1	1	0	7
18	С.К.	2	2	2	2	1	9
19	С.Л.	1	1	0	1	0	3
20	С.Н.	2	1	1	1	1	6

Полученные результаты подвергались количественной и качественной обработке. Статистическая достоверность данных сравнительного анализа рассматривалась по φ- критерию угловое преобразование Фишера.

Эмпирическое значение φ _эмп подсчитывалось по формул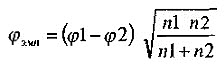е:

, где

φ1 – величина, соответствующая большей процентной доле, φ2 – величина, соответствующая меньшей процентной доле, n1 – количество наблюдений в выборке 1, n2 – количество наблюдений в выборке 2.

Критические значения для 5%, 1%, 0,1% уровней значимости имеют фиксированную величину и составляют соответственно:

φ _кр = 1,64 для р ≤ 0,05; φ _кр = 2,31 для р ≤ 0,01; φ _кр = 2,81 для р ≤ 0,001.

Сравнительный анализ уровня формирования геометрических понятий у детей ЭГ и КГ на контрольном этапе эксперимента представлен в таблице 7.
Таблица 7 - Сравнительная таблица уровней формирования геометрических понятий у детей КГ и ЭГ на контрольном этапе эксперимента (в %)

Уровень развития умения	Экспериментальная группа n=20		Контрольная группа n=20		φ - критерий Фишера в сравнении с ЭГ
Уровень развития умения	Кол-во детей	Процентное соотношение	Кол-во детей	Процентное соотношение	φ - критерий Фишера в сравнении с ЭГ
Высокий	10	50%	5	25%	1,657*
Средний	9	45%	10	50%	0,316
Низкий	1	5%	5	25%	1,885*

Примечание:

* - различия статистически значимы при φ_кр =1,64 для р≤ 0,05;

** - различия статистически значимы при φ_кр=2,31 для р≤ 0,01;

*** - различия статистически значимы при φ_кр =2,81 для р≤ 0,001.
Результаты свидетельствуют о том, что после формирующего этапа эксперимента детей с низким уровнем формирования геометрических понятий в экспериментальной группе выявлено только 5% (1 чел.). Значительно увеличилось число школьников с высоким уровнем формирования геометрических понятий в экспериментальной группе. С помощью φ- критерия угловое преобразование Фишера обнаружены статистически значимые различия между контрольной и экспериментальной группами в высоком и низком уровнях формирования геометрических понятий (φ_эмп = 1,657 при p ≤ 0,05; φ_эмп = 1,885 при p ≤ 0,05).

В процессе выполнения заданий в контрольной группе наблюдались трудности при выполнении заданий. В экспериментальной группе ответы детей стали более точными и правильными. Дети активнее анализировали свою работу. На вопросы стали отвечать полными ответами.

На основе этих данных можно говорить об эффективности проведенной в экспериментальной группе работы по формированию геометрических понятий.

Подробное и наглядное сравнение уровней формирования геометрических понятий в ЭГ и КГ на контрольном этапе эксперимента представлено на рисунке 3.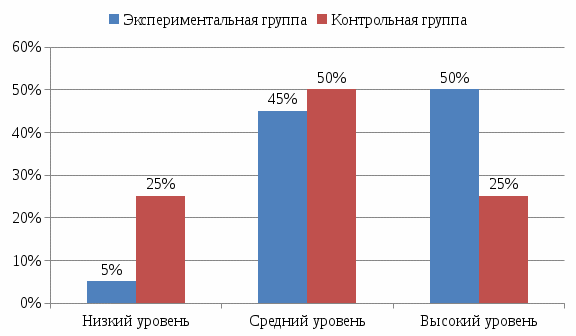

Рисунок 3 - Сравнительная диаграмма уровня формирования геометрических понятий у детей КГ и ЭГ на контрольном этапе эксперимента (в %)
Сравнительный анализ данных контрольной и экспериментальной групп на констатирующем и контрольном этапах эксперимента показал повышение уровня формирования геометрических понятий в обеих группах, однако динамика повышения в ЭГ выше, чем в контрольной КГ.

В ЭГ на контрольном этапе эксперимента детей с высоким уровнем формирования геометрических понятий стало на 35% больше, с низким уровнем количество детей ЭГ сократилось на 20%. В КГ изменения менее успешны: количество детей с высоким уровнем формирования геометрических понятий стало на 5% больше, с низким уровнем количество детей ЭГ сократилось на такое же количество (см. рис. 4).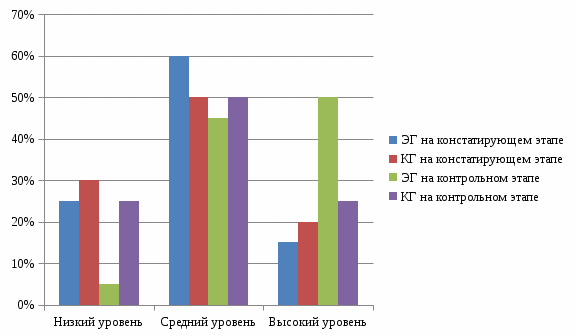

Рисунок 4 - Сравнительная диаграмма уровня формирования геометрических понятий у детей ЭГ и КГ на констатирующем и контрольном этапах эксперимента (в %)
Используя U-критерий Манна-Уитни, мы подтвердили статистическую значимость произошедших изменений у детей ЭГ на контрольном этапе эксперимента и доказали, что изменения в КГ статистически не значимы.

Гипотезы U - критерия Манна-Уитни

H0: Уровень признака в группе 2 не ниже уровня признака в группе 1.

H1: Уровень признака в группе 2 ниже уровня признака в группе 1.

В каждом случае в качестве группой 2 были взяты данные констатирующего этапа, так как именно они должны были быть ниже.

Критические значения (U_Кр)

p≤0.01 114 p≤0.05 138

Для начала были использованы данные экспериментальной группы. Подробности расчёта представлены в таблице 8.

Таблица 8 - Результаты математической обработки данных по уровню формирования геометрических понятий у детей ЭГ

№	Выборка 1	Ранг 1	Выборка 2	Ранг 2
1	4	5	4	5
2	10	39	9	32.5
3	9	32.5	6	13
4	5	7	2	1
5	9	32.5	7	20.5
6	8	25	6	13
7	9	32.5	6	13
8	10	39	9	32.5
9	8	25	6	13
10	6	13	3	2.5
11	9	32.5	7	20.5
12	8	25	6	13
13	10	39	9	32.5
14	9	32.5	7	20.5
15	8	25	6	13
16	6	13	3	2.5
17	9	32.5	7	20.5
18	9	32.5	6	13
19	6	13	4	5
20	8	25	6	13
Суммы:		520.5		299.5

Результат: U_Эмп = 89,5

Полученное эмпирическое значение U_эмп(89,5) находится в зоне значимости.

Таким образом, Но откланяется, принимается Н1. Уровень признака в группе 2 ниже уровня признака в группе 1. То есть между результатами тестов в экспериментальной группе до и после проведенной нами работы, существуют достоверные различия.

Затем таким же образом, мы обработали данные по контрольной группе. Подробности расчёта представлены в таблице 9.

Таблица 9 - Результаты математической обработки данных по уровню формирования геометрических понятий у детей КГ

№	Выборка 1	Ранг 1	Выборка 2	Ранг 2
1	5	12	4	8
2	6	18	6	18
3	9	36	9	36
4	7	27	7	27
5	7	27	6	18
6	9	36	9	36
7	3	3	3	3
8	6	18	6	18
9	9	36	7	27
10	5	12	4	8
11	7	27	7	27
12	4	8	3	3
13	7	27	6	18
14	9	36	9	36
15	6	18	6	18
16	4	8	4	8
17	7	27	7	27
18	9	36	9	36
19	3	3	3	3
20	6	18	5	12
Суммы:		433		387

Результат: U_Эмп = 177

Полученное эмпирическое значение U_эмп(177) находится в зоне незначимости.

Таким образом, Но принимается. Уровень признака в группе 2 не ниже уровня признака в группе 1. То есть между результатами тестов в контрольной группе не существует достоверных различий.

Анализ результатов показал, что только в ЭГ изменения после проведенной работы на формирующем этапе эксперимента статистически значимы и достоверны.

1 2 3 4 5 6 7 8