ДЕТАЛИ МАШИН И ОК. 10. Детали машин Классификация деталей машин

• Название: 10. Детали машин Классификация деталей машин
• Дата: 22.04.2023
• Размер: 2.11 Mb.
• Имя файла: ДЕТАЛИ МАШИН И ОК.docx
• Тип: Документы; #1081321
• страница: 12 из 20

 Основная теорема зубчатого зацепления.

Пусть имеется пара зубчатых колес с центрами О₁и О₂,вращающихся соответственно с угловыми скоростями   и   На рис.18, а показаны сложения, которые последовательно занимает пара сопряженных (эвольвентных) зубьев в процессе их зацепления; прямую О₁О₂называют межосевой линией зубчатой передачи. Проведем в точках касания зубьев К₁, К₂, К₃, ... общие нормали к профилям. Все эти нормали NN должны пересекать межосевую линию О₁О₂в постоянной точке Р. Эту точку называют полюсом зацепления;ее положение на межосевой линииопределяется отношением уг­ловых скоростей колес, т.е. их отношением: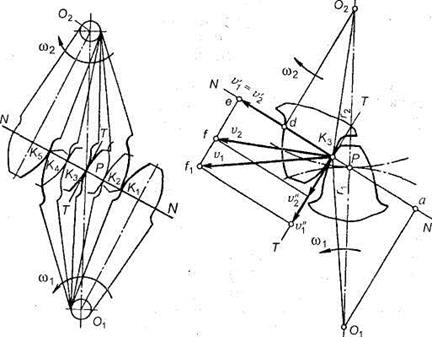



 



а)б)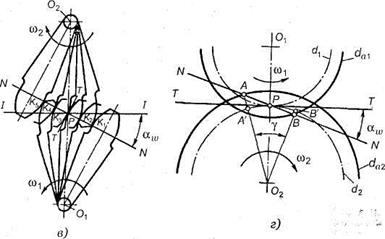



Рис. 18. Элементы зубчатого зацепления

 

Основную теорему зацепленияможно сформулировать так: общая нор­маль к профилям зубьев в точке их касания пересекает межосевую линию в точке Р, называемой полюсом зацепления и делящей межосевое расстояние на отрезки, обратно пропорционально угловым скоростям.

Следствие: для обеспечения постоянного передаточного отношения по­ложение полюса Р на линии центров должно быть постоянным.

В процессе работы сопряженных (эвольвентных) профилей точка их касания все время перемещается по прямой NN. Эту прямую называют линией зацепления.

Место (точку) входа в зацепление и выхода из него сопряженных зубь­ев можно определить при следующем геометрическом построении.

Длина линии зацепления q_a— отрезок линии зацепления, отсекаемый окружностями вершин зубьев сопряженных колес. Он определяет начало иконец зацепления пары сопряженных зубьев. Длина зацепления — актив­ная часть линии зацепления.

Коэффициент торцового перекрытия  — отношение длины линии за­цепления к шагу: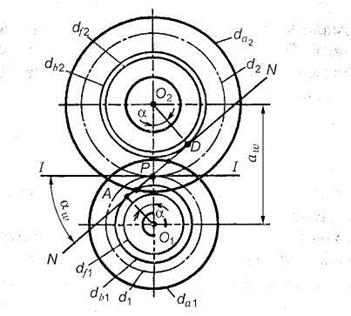



Рис. 19. Геометрические параметры зубчатой передачи

 

В современном машиностроении для построения сопряженных профилей применяют ограниченное число кривых.

Профили зубьев должны быть технологичными, т.е. такими, чтобы их можно было получить в производственных условиях наиболее простыми методами. Из теоретически возможных профилей преимущественное применение получили эвольвентные профили(см. рис. 18, б). Это обусловлено тем, что эвольвентное зацепление, будучи достаточно простым геометрически, имеет существенные технологические и эксплуатационные преимущества: эвольвентные зубья могут быть весьма точно нарезаны относительно простым инструментом с прямолинейными режущими кромками, причем одним инструментом можно нарезать колеса с различным числом зубьев; эвольвентные передачи нечувствительны к отклонениям межосевого расстояния от его теоретического значения; они допускают модификацию профиля зубьев, сводящуюся к выбору оптимальных участков эвольвенты, обеспечивающих наилучшие работоспособность, к.п.д. и другие. Это зацепление может быть использовано и в сменных колесах. Эвольвентное зацепление предложено Эйлером более 200 лет назад в 1760 г.

В зацеплении М.Л. Новикова, предложенном в 1954 г., рабочие профили зубьев очерчены дуга­ми окружностей (рис. 20, 21). Передачи Новикова имеют повышенную (в 1,5...2 раза), по сравнению с эвольвентными, контактную несущую способность, но пониженную изгибную выносливость. Ввиду сложности изготовления и монтажа передачи с зацеплением Новикова пока нашли применение только в специальном машиностроении.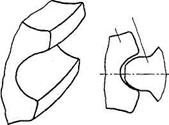



Рис. 20. Колесо с зацеплением М. Л. Новикова

 

Краткие сведения о корригировании зацеплений

Форма эвольвентного профиля зубьев при заданном угле инстру­мента   и модуле зависит от числа зубьев z (рис. 23): с уменьшением чис­ла зубьев увеличивается кривизна эвольвентного профиля и соответствен­но уменьшается толщина зубьев у основания и вершины.

Если число зубьев z меньше некоторого предельного значения z_min, то при нарезании зубьев происходит подрезание ножек зуба (рис. 23, z= 10), в результате чего в опасном сечении зуб значительно ослабляется, снижа­ется его прочность на изгиб, а также уменьшается рабочая часть ножки, что увеличивает изнашивание зубьев и уменьшает коэффициент их пере­крытия.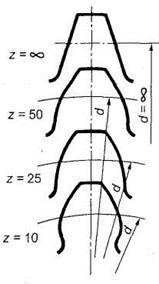



Рис.23. Формы зубьев  эвольвентного профиля

 

Минимальное число зубьев шестерни, у которой исключено подреза­ние зубьев, без сдвига инструмента реечного типа, определяется по фор­муле  , где  — угол профиля зуба рейки. Для стандартного зацепления  = 20⁰, z_min= 17. При больших окруж­ных скоростях передачи для уменьшения шума для гедукторов   принимают   число   зубьев   шестерни z = 20   30.

Для устранения явлений подрезания зубьев и улуч­шения параметров передачи применяют корригирование. Корригирование зубьев производят на обычных станках стандартным инструментом. Разница в из­готовлении зубчатых колес с некорригированными и корригированными зубьями заключается в том, что для последних инструмент устанавливают с некоторым дополнительным смещением по отношению к оси заготовки.

Виды повреждений и разрушений зубьев колес

Поломка зубьев.Этот вид разрушения зубьев полностью выводит передачу из строя, нередко сопровождающегося повреждениями смежных узлов и деталей машины (валов, подшипников и др.), вследствие заклинивающего действия выломавшихся кусков зубьев. 

Усталостная поломка зубьев колес является конечным результатом зарождения в них и развития до своих критических размеров усталостной трещины. Усталостные трещины появляются у корня зуба со стороны его растянутых волокон, где действуют наибольшие растягивающие напряжения, связанные с концентрацией напряжений, возникающей в переходной зоне зуба.

Выкрашивание (питтинг) рабочих поверхностей зубьев.Этот вид повреждения зубьев является наиболее серьёзным и распространённым дефектом поверхности зубьев даже для закрытых хорошо смазываемых и защищённых от загрязнения передач и нарушает нормальную работу всей передачи, но не выводит ее из строя полностью. Выкрашивание носит усталостный характер и вызвано контактными напряжениями, которые изменяются по отнулевому пульсирующему циклу. Выкрашивание заключается в появлении на рабочих поверхностях зубьев вблизи полюсной линии небольших углублений, напоминающих оспинки, которые потом растут, распространяясь на всю поверхность ножки зуба, превращаясь в раковины

Для предупреждения выкрашивания необходимо повышать твёрдость материала  термообработкой либо повышать степень точности передачи, а также правильно назначать размеры из расчёта на усталость по контактным напряжениям (контактную выносливость).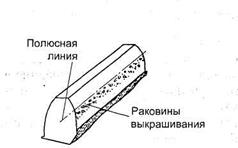



 

Рис.26. Виды разрушений зубьев. Уста­лостное выкрашивание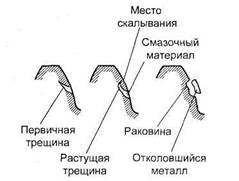

 



Рис. 27. Процесс образования усталост­ных раковин в закрытой передаче

 

Изнашивание (истирание) зубьевчаще наблюдается в открытых передачах, чем в закрытых, заключается в истирании рабочих поверхностей (рис. 28) вследствие попадания в зону зацепления металлических частиц, пыли, гря­зи (абразивное изнашивание). Встречается также и в  закрытых передачах, но находящихся в засорённой среде: в горных, дорожных, строительных, транспортных машинах. Является основной причиной выхода из строя передач при плохой смазке. Усталостное контактное выкрашивание зубьев в таких передачах не наблюдается, так как истирание опережает процесс образования усталостных повреждений в поверхностном слое.

Заедание зубьев.Наблюдается как в открытых, так и в закрытых высокоскоростных, тяжело нагруженных передачах и возникает при высоких контактных напряжениях и разрыве или отсутствии масляной пленки, разъединяющей взаимодействующие зубья колес.

Расчет зубьев цилиндрической прямозубой передачи на изгиб

Ниже излагается упрощенный метод расчета зуба на изгиб, осно­ванный на положениях сопротивления материалов.

На рис. 34 показаны схема зацепления двух зубьев в полюсе и силы, действующие на зубья колес со стороны шестерни; трение не учитывается. Нормальная сила F_nраскладывается на две составляющие: окружную силу F_tи радиальную или распорную — F_r.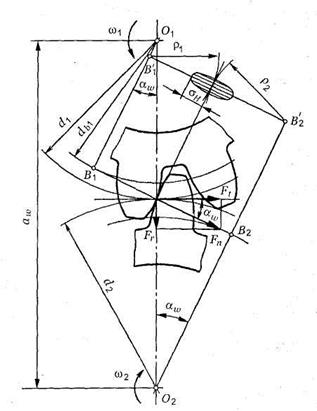



Рис. 34. Усилия в зацеплении прямозубой цилиндрической передачи

 

На рис.35 показан профиль балки равного сопротивления (s — тол­щина зуба в опасном сечении; l — плечо изгибающей силы;   — длина зуба; F_n— нормальная сила, действующая на зуб).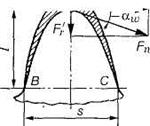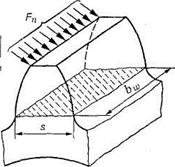


     

Рис.35. Схема расчета зубьев на изгиб

 

Определим силы в опасном сечении корня зуба. Разложим силу F_nв точке Ана две составляющие:  и  , условно принимаем, что сила F_nприложена только к одному зубу (перекрытием пренебрегаем), а сила F_tравна окружной силе на начальной окружности.

Сила  изгибает зуб, а сила  сжимает его. Из рис. 35 находим

=F_ncos ;         =F_nsin

где   — угол направления нормальной силы F_n, приложенной у вершины, который несколько больше угла зацепления  ;  F_n-F_t/cos  — нормаль­ная сила.

Исходя из изложенного выше, за расчетное напряжение принима­ют напряжения на растянутой стороне зуба:

                                                                            (1)

Для опасного сечения ВС условие прочности



где σ_F — напряжение изгиба в опасном сечении корня зуба; W — осевой момент сопротивления; A= s— площадь сечения ножки зуба.

Выразим I и s в долях модуля зубьев: l= km; s = cm, где ки с — коэффи­циенты, зависящие от формы зуба, т.е. от угла  и числа зубьев Z.

Тогда изгибающий момент в опасном сечении

M_B=F_t∙l=F_t∙km;

осевой момент сопротивления прямоугольного сечения зуба



Подставим в формулу (2) входящие в него параметры М_Ии W, введем коэффициенты расчетной нагрузки   (табл. 6), K_FV (табл. 7) и теоре­тический коэффициент концентрации напряжений К_Т.

В результате получим окончательную формулу проверочного расчета прямозубой передачи на усталость при изгибе



где Y_F— коэффициент учитывающий форму зуба и концентрацию напря­жений

 Расчет цилиндрической прямозубой передачи на контактную прочность

При выводе формул приняты следующие допущения: зубья рассматри­вают как два находящихся в контакте цилиндра с параллельными образую­щими (радиусы этих цилиндров принимают равными радиусам кривизны профилей зубьев в полюсе зацепления); нагрузку считают равномерно рас­пределенной по длине зуба; контактирующие профили предполагают не­разделенными масляной пленкой.

На основании этих допущений к расчету зубчатых колес можно приме­нить результаты исследований на контактную прочность цилиндрических роликов. Наибольшие нормальные контактные напряжения возникают в точках, лежащих на очень малой глубине под линией контакта по формуле Герца—Беляева:



где q — расчетная удельная нормальная нагрузка; E_пр — приведенный мо­дуль упругости материалов зубьев;   — приведенный радиус кривизны профилей зубьев шестерни и колеса;   — коэффициент Пуассона. Для прямозубых колес без учета коэффициентов нагрузки

,                                                                                          (17)

где   — нормальная сила, действующая на зуб (см. рис. 35); F_t — окружная сила;   — суммарная длина контактной линии (для прямозубых передач ;   — ширина венца, так как  ; здесь   — коэффициент, учитывающий непостоянство суммарной длины контактной линии);  — коэффициент перекрытия.

Приведенный модуль упругости Е_пр=2Е₁Е₂/(Е₁+Е₂), где E₁ и E₂ — мо­дули упругости материалов шестерни и колеса.

Зубья рассматриваются как цилиндры длиной b_a (ширина зубчатого ко­леса) и радиусов   и  , где



Приведенный радиус кривизны зубьев в полюсе



Здесь знак «плюс» для внешнего зацепления, знак «минус» — для внут­реннего зацепления.                                                  

Тогда формула проектного расчета для определения межосевого рас­стояния закрытых цилиндрических передач



Допускаемые контактные напряжения (МПа) при расчете рабочих поверхностей на усталостное выкрашивание рассчитываются по формуле

,

Где   — предел выносливости рабочих поверхностей зубьев (табл. 11), соответствующий базовому числу циклов перемены напряжений N_Hlim, МПа (база испытаний N_H0 определяется по табл. 12);

S_H  — коэффициент безопасности (S_H= 1,1 при нормализации, улучше­нии или объемной закалке; при поверхностной закалке и цементации S_H=1,2);

Z_R — коэффициент, учитывающий шероховатость сопряженных по­верхностей зубьев (Z_R=1 0,9);

K_HL — коэффициент долговечности, который учитывает влияние срока службы, режима нагрузки передачи и возможность повышения допускае­мых напряжений для кратковременно работающих передач.

Вопросы для самопроверки

- Каковы основные достоинства и недостатки  зубчатых передач  по сравнению с другими передачами?

- По каким признакам классифицируют зубчатые передачи?

- Чем отличается закрытая передача от открытой?

- Перечислите достоинства зубчатой передачи по сравнению с фрикционной передачей.

- Почему в зубчатых передачах сохраняется постоянным передаточ­ное отношение?

- Что такое эвольвента окружности и какими свойствами, полезными для зубчатых зацеплений, она обладает?

- Какие окружности называют начальными, какие делительными?

- Что называется шагом, модулем и углом зацепления?

- Что такое исходный профиль рейки эвольвентного зацепления?

- В чем сущность основной теоремы зацепления?

- Что такое эвольвента окружности и какими свойствами она обладает?

- Почему эвольвентное зацепление имеет преимущественное применение?

- Что называют полюсом зацепления, линией зацепления и углом зацепления?

- Как определить на линии зацепления точки, соответствующие началу и концу зацепления одной пары зубьев?

- Какие окружности зубчатых передач называют начальными и какие окружности зубчатых колес называют делительными? В каких зубчатых передачах они совпадают?

- Что понимают под коэффициентом торцового перекрытия? Как влияет его величина на работу зубчатой передачи?

- Каково влияние числа зубьев на их форму и прочность?

- Как возникает подрезание зубьев при нарезании их инструментом реечного типа?

- С какой целью производят смазывание зубчатых передач?

- Какие основные факторы влияют на КПД зубчатых передач?

- Каковы области применения прямозубых и косозубых передач?

- Уточните основное условие для обеспечения постоянства передаточного числа зубчатой передачи.

- Каковы сравнительные достоинства прямозубых и косозубых колёс?

- Как определяется передаточное отношение  и передаточное число?

- Каковы главные виды разрушений зубчатых колёс?

- Какие силы действуют в зубчатом зацеплении?

- Какие допущения принимаются при расчёте зубьев на контактную прочность?

- По какой расчётной схеме выполняется расчёт зубьев на изгиб?

- Какие зубья прочнее на изгиб — колеса или шестерни?

- По какой причине ограничивают угол наклона зубьев в косозубых передачах?

- Почему косозубые передачи прочнее, чем прямозубые?

- Чем вызвана плавность работы косозубых передач?

Планетарные зубчатые передачи

Передачи, имеющие зубчатые или фрикционные колеса с перемещающимися осям, называют планетарными. Эти подвижные колёса подобно планетам Солнечной системы вращаются вокруг своих осей и одновременно перемещаются вместе с осями, совершая плоское движение,  называются они сателлитами (лат. satellitum – спутник). Подвижные колёса катятся по центральным колёсам (их иногда называют солнечными колёсами), имея с ними внешнее, а с корончатым колесом внутреннее зацепление. Оси сателлитов закреплены в водиле и вращаются вместе с ним вокруг центральной оси.

Наиболее распространена зубчатая однорядная планетарная передача (рис.15). Она состоит из центрального колеса 1 с наружными зубьями (эпициклического колеса или эпицикла), неподвижного (центрального) колеса 2 с внутренними зубьями (солнечного колеса) и водила h на котором закреплены оси планетарных колес g (или сателлитов).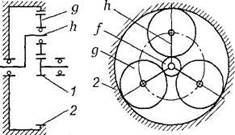



Рис.15. Планетарная передача

 

Водило вместе с сателлитами вращается вокруг центральной оси, а са­теллиты обкатываются по центральным колесам и вращаются вокруг своих осей, совершая движения, подобные движению планет. При неподвижном колесе 2 движение передается от колеса 1 к водилу h или наоборот.

Достоинства и недостатки планетарных передач

Основное достоинство—- Планетарный принцип позволяет получать большие передаточные чис­ла (до тысячи и больше) без применения многоступенчатых передач.

- Эти передачи удобно компоновть благодаря соосности ведущего и ведомого валов.

- Эти передачи компактные и имеют малую массу.

- Сателлиты в планетарной передаче расположены симметрично, а это снижает нагрузки на опоры (силы в передаче взаимно уравновешиваются), что приводит к снижению потерь и упрощает конструкцию опор.

- Эти передачи работают с меньшим шумом, чем обычные зубчатые и имеют более лёгкое управление и регулирование скорости;

- Имеют высокий КПД при относительно больших передаточных числах;

Основные недостатки:

- повышенные требования к точности изготовле­ния и монтажа (для обеспечения сборки планетарных передач необходимо соблюдать условие соосности (совпадение геометрических центров колёс);

Особенности проектирования и расчёта планетарных передач связаны с наличием избыточных кинематических связей (нескольких сателлитов). Предельно возможное число сателлитов в одном планетарном ряду ограничивается условием соседства, которое гласит: число сателлитов в планетарном ряду должно быть таким, чтобы соседние сателлиты не касались друг друга.